垃圾词匹配算法-对比与概述
前面工作接到一个项目需求,需要对交流消息做垃圾词(敏感词)做处理,特地去了解了一波敏感词匹配算法,这里对算法调研做一下文档记录,方便后续需求
文本搜索与替换
描述及实现理论
这种方式是最简单的,就是循环把每个敏感词在目标文本中从头到尾搜索一遍,如果有文本高亮或替换的话,那就找到一个就处理一个
优点
算法简单,对于开发人员来说,简单的算法会使代码实现上简单,开发难度最小
缺点
效率太低,因为循环每个敏感词,所以当敏感词很多、目标文本很长时,其效率可以说是该算法的致命问题
前缀树匹配
描述
字典树又称前缀树,Trie树,是一种树形结构,是一种哈希树的变种,一种有序树,用于保存关联数组,其中的键通常是字符串,且键是由节点在树中的位置决定的。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计、搜索提示
三个基本性质
-
根节点不包含字符,除根节点外每个节点只包含一个字符
-
从根节点到某个节点,路径上所有的字符连接起来,就是这个节点所对应的字符串
-
每个节点的子节点所包含的字符都不同
实现理论
构建敏感词前缀树,三个指针,分别为指针1,指针2,指针3
-
指针1:初始指向前缀树的根。当指针2指向的字符与其指向的前缀树中的字符想匹配时,则一起移动,当命中一个敏感词或者无法匹配下去时,则返回根
-
指针2:其走到字符串尽头时说明比较结束。其用于保存当前正在比较的字符串的首个字符的位置,若匹配到某个字符不吻合,则其会移动到下一个字符位置
-
指针3:每次都和指针1指向的字符比较,若温和,则与指针一一起移动,否则,则继续移动
优点
是一种树形结构,利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,提高查询效率
缺点
一旦匹配失败,又要从根开始
改进方案
利用KMP算法防止匹配失败时字符串回溯(最大最小前缀),改进了之后其实就像AC自动机了
Aho-Corasick自动机算法
描述
AC自动机首先将模式组记录为Trie字典树的形式,以节点表示不同状态,边上标以字母表中的字符,表示状态的转移。根节点状态记为0状态,表示起始状态。当一个状态处有一个模式串终结则标记一下
场景
AC算法主要是解决多字符串匹配问题,比如字符串ushers,作为长字符串, 多模式串:he/ she/ hers/ his ,作为匹配串。要解决的问题就是:在长字符串ushers中,是否包含多模式串(也就是ushers中,是否存在he,是否存在she…等等)
所以也常常被用于处理敏感词匹配问题
实现理论
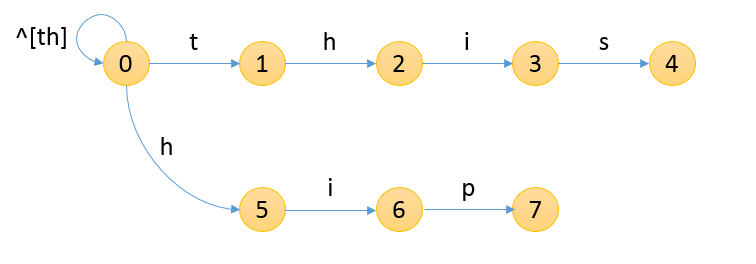
匹配的过程是:从0状态起点开始,以字符流输入,进行适当的状态转移,如果可以抵达某一标记终结的状态,则成功匹配模式,串值为从0到终结点的路径
按照传统的说法,状态机有三个主要函数支撑:goto(状态正常转移),fail(状态失配转移),output(传回匹配结果),而我认为与其规定是具体的函数,倒不如说是三个功能的模块,有不同于函数的实现形式
goto是自动机基本的状态转移过程,很好想,就是在建立Trie树时让每个状态维护一组指针(广义的),使得在每一状态对于输入都可以正确转移,没有对应的则报错(现在回答刚才的问题,什么是失配?失配就是一个状态接受了无法转移的字符,记fail)。除了字典树中的树枝以外,还有一个转移就是在开始节点,对于不能流进自动机的字符,不报错而是再一次转到开始节点,很好理解,对于待匹配串λthis,λ为不含t,h的任意串,真正的模式匹配是在去除了它以后开始的
正常的状态流转已经建立好了,现在看失配时我们的状态流何去何从。举一个栗子,如果输入thip这个串,状态的流转应该如下
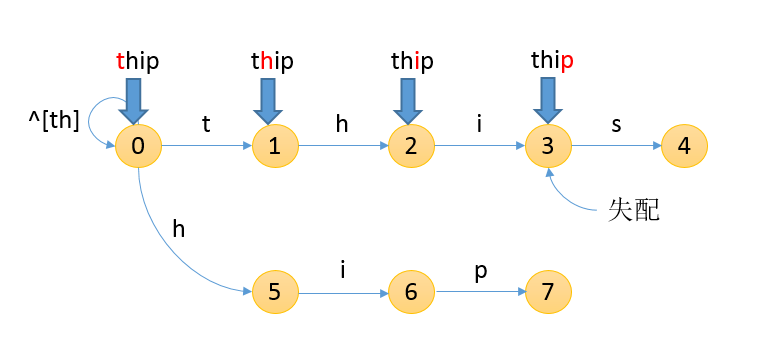
那3状态处报错后应该怎么处理呢?最好想的方法当然是错开一位,再从头开始匹配(这种方法就像一位老人家曾经说过,太年轻太简单,有时还很幼稚),AC二位的办法是——利用图中的关系计算出一套跳转关系——在x点处失配的串不打回开头来过,而是跳到y点——继续匹配当前字符。这套规则叫做失配函数,也就是fail功能模块。要点在于当前字符不向前回溯,想想着很适合字符流的关键字匹配对不对
接着说一下3状态的失配跳转在6状态,先不用管怎么得到的,先想想这个过程:3得到p字符,失配,凭goto无法转移状态,使用失配时通用的fail,状态跳至6,接受p——还是这个字符,成功匹配到终结状态7。单趟遍历目标串完成
正式开始之前请认真思考这个情况:已知2状态的失配跳转为5,怎么求3状态的失配跳转?从图中很容易看出,2通过i流向3,而5恰有对i的goto,自然地,3失配时可以跳转至6
优点
-
AC巧妙的将字符匹配转换为了状态转移
-
同时与所有字典串匹配,一般的时间复杂度为O(字符串长度+所有匹配数量)
DFA算法(自动机算法)
描述
DFA是一种计算模型,数据源是一个有限个集合,通过当前状态和事件来确定下一个状态,即 状态+事件=下一状态,由此逐步构建一个有向图,其中的节点就是状态,所以在DFA算法中只有查找和判断,没有复杂的计算,从而提高算法效率
实现理论
-
构造数据结构
将敏感词转换成树结构,举例有着王八蛋和王八羔子两个敏感词,这两个词的二叉树构造为
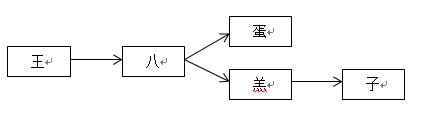
把每个敏感词字符串拆散成字符,再存储到HashMap(其他语言可用字典实现hashmap)中,如下
{
"王": {
"isend": False,
"八": {
"isend": False,
"蛋": {
"isend": True,
},
"羔": {
"isend": False,
"子": {
"isend": True,
}
},
}
}
} -
判断逻辑
将每个词的第一个字符作为key,vlue则是另一个HashMap,value对应的HashMap的key为第二个字符,如果还有第三个字符,则存储到以第二个字符为key的value中,当然这个value还是一个HashMap,以此类推下去,直到最后一个字符,当然最后一个字符对应的value也是HashMap,只不过这个HashMap只需要存储一个结束标志就行了
上面最后就是保存了一个{"isend": True} 的HashMap,来标识这个value对应的key是敏感词的最后一个字符
先从文本的第一个字开始检查,比如 你个王八羔子 ,第一个字 你 ,在树的第一层找不到这个节点,那么继续找第二个字,到了 王 的时候,第一层节点找到了,那么接着下一层节点中查找 八 ,同时判断这个节点是不是结尾节点,若是结尾节点,则匹配成功了,反之继续匹配
优点
效率高
缺点
-
理论算法太过复杂,开发成本很大
-
该算法巨耗内存,而且启动很慢
XDMP算法
核心思路
-
首先扫描文章里面的每一个字符,只有当某一个字符是脏字表中任意一个脏词的第一个字符(称为“起始符”),我们才试图看看接下来是否是脏字(触发检索),但是我们也不是毫无头绪的就开始循环脏字表的每一个词条
-
我们往后检索一个字符,先看一下这个字符是否是脏字表里面的任意一个字符,如果不是,就表明不可能是脏字表中的任何一个条目,就可以退出了
-
如果是,我们就取从第一个被检出字符到目前扫描到的字符之间的字符串,求哈希值,看看能否从哈希表中检出一个脏词
-
如果检出了,那就大功告成,否则继续检索后面一个字符(二三步骤),直至找不到,或者超出脏字表条目最大的长度
-
如果都找不到,或者超长,那么接下来就回到刚才的那个“起始符”后一个字符继续扫描(重复1、2),直至整个文章结束
关键点
-
扫描,指扫描文章,看看是否有需要和脏字表开始进行对比的情况
-
检索,指已经发现可能存在情况了,在将文本和脏字表进行对比的过程
-
起始符,指脏字表中条目中的第一个字符
优化理论
如果我们只要扫描,不需要检索就可以完成任务,那一定是最快的,不过目前没有找到这样的算法 又或者,如果我们扫描一遍,而检索全中,那也很不错,很不幸,还是没见过 很明显,扫描不应该多于1遍,否则肯定效率不可能高。那么检索就是算法的关键了!拆开来,提高检索质量有下列几个方式:
-
尽可能不触发检索
-
如果确实需要触发检索了,那么每次触发检索的时候,要尽可能减少检索所需要遍历的字符数量
-
每次对比脏字表的时候,减少运算量
理论分析及优点
-
一次扫描
-
只要发现“起始符”就触发检索
-
检索的时候,需要遍历的字符数是 1+2+3+...+n,这里的n是被命中的脏词的长度,或者最接近的长度
-
每次检索,需要重复计算HashCode,不要忘了,计算HashCode,也是需要扫描字符串的,也就是又要遍历1+2+3+..+n个字符
TTMP(字符串多模式精确匹配)
描述
分析XDMP算法会发现一些问题,如下:
-
难道每次遇到“起始符”了,就一定要触发检索吗?哎呀妈呀,这个也要检索(因为脏字表里面可能有MB)
-
难道每次触发检索,都非得要检索长度为1的,长度为2的,长度为3的……直到检索成功,或者出现非脏字表字符的时候吗
-
难道每次检索,我们都需要把特定长度的待检文本截取出来吗
-
难道每次检索,都需要从头开始计算哈希值吗?不能利用同一次触发检索后,上一次检索的哈希值,来减少本次计算的不必要运算量吗
理论
XDMP算法的最大问题就是遇到起始符就开始匹配,计算哈希值,TTMP算法就逆向匹配,在触发对关键字的检索时,从后面往前面检索。比如说:
脏字表:wxyz、yz 待检文本: wxyza 当我们遇到了结束符z的时候,我们会回过头来查看刚才到底都遇到了什么文字。由于我们之前的扫描已经得到了两个“起始符”的相关信息,因此我们只要按发现起始符的逆序找 yz和wxyz。于是,最终我们命中的关键字是yz,而不是最先遇到的wxyz
优点
-
找到的一定是最短的匹配
-
在分析正常文本的时候,效率可能相对会更高
分析
重点说一下为什么效率可能会相对更高,这里有两个原因
-
如果我们的脏字表存在以某一个有n个短模式X作为结尾的其他模式,例如AX、BX,由于算法的特殊关系,是不可能进行AX、BX扫描的。这样的话,我们可以少算若干个字符的运算量
-
对于正常文本,以及正常的脏字表,有如下特性:
-
文本中出现脏字条目命中的概率是非常低的,也就是说,大多数遇到起始符的情况,到最后都不见得能遇到结束符。于是在扫描到起始符就开始计算哈希值,很可能是得不偿失的(大多时候预先的计算是白做的),因此我们很可能选择在触发检索之后,再重新回过头来计算哈希值。同样是在触发检索之后,再重新计算哈希值的情况下,B模式比F模式所需要额外损失的性能就会更小
-
脏字表中的词条通常都是小字符串占多数,而且通常比较有可能会有交集的情况,比如说ABC和C。在此情况下,如果从后往前搜索,实际上ABC这个条目是永远也不会被命中的。换句话说,B模式会自动达到使得脏字表最小化的实际效果,而不需要进行一个取交集的运算过程,包括初始化的时候和进行扫描的时候,都不会有额外的性能损失(不预先计算哈希值的情况),或者至少性能损失较小(预先计算哈希值的情况)。当然了,这样会占用一些额外的不必要的空间,不过一般来说脏字表要超过1万个条目都很难,1万个条目撑死了也就占用100k
缺点
-
要做最大匹配,意味着要付出更高昂的额外计算成本
-
由于是逆顺序检索,如果我们选择遇到起始符就预先计算哈希值,就很有可能做了一些不必要的运算,即使是在命中的情况下。考虑: 脏字表:ABC、C 待建文本: ABC 则在遇到A的时候,就会开始计算哈希值,直到C字符。但是可以看到,对AB进行哈希值计算,很有可能就是不必要的 关于这个缺点,其实只是“眼看着还有白费的运算无法消除”而已,实际上相对可能还是更快的
KMP单模匹配算法
描述
KMP算法是由Knuth,Morris,Pratt共同提出的算法,专门用来解决模式串的匹配,无论目标序列和模式串是什么样子的,都可以在线性时间内完成,而且也不会发生退化,是一个非常优秀的算法,时间复杂度的上界是O(n+m)
解决的问题
普通的字符串匹配算法,暴力的字符串匹配算法,其实就是个组合的过程,一般来说有两个量,一个是i一个是j,i在目标串上移动,j在模式串上移动,如果target[i]==text[j],那么i++,j++,如果不等于,不好意思,请 i 回到开始匹配成功的下一个位置,j=0,重复匹配,可见这样的算法的复杂度是O(n*m),相当地慢,这种算法没什么技巧
如果学过数据结构的人都知道,对于字符串匹配还有比暴力法好得多的一种算法,那就是散列法,散列法通过算字符串的散列值来匹配模式串,我们只用把模式串散列一次然后就可以把维持m长度的指针从目标串的0位置匹配到n-m位置就可以了,这个算法的复杂度是上界是O(n),看上去很不错,但是事实上如果模式串很大的话,我们要找到一个很好的散列函数(第一个保证散列值都是唯一的(不可能用链表法,因为可能散列值会很大,重复很多效率就下降了),散列值最好是能从上一个推出下一个的),而且要开辟一个相当大的空间来储存散列值
KMP算法就是一个很好的散列的算法
理论
KMP算法的根本目的就是想让i不后退(散列法也是这样想的),这就要求我们把匹配过的信息进行储存,KMP算法用到一个next数组,是整个算法的关键
讲next数组之前我们先来明白一下什么是模式串的前缀后缀最长公共长度,先来看一个表:
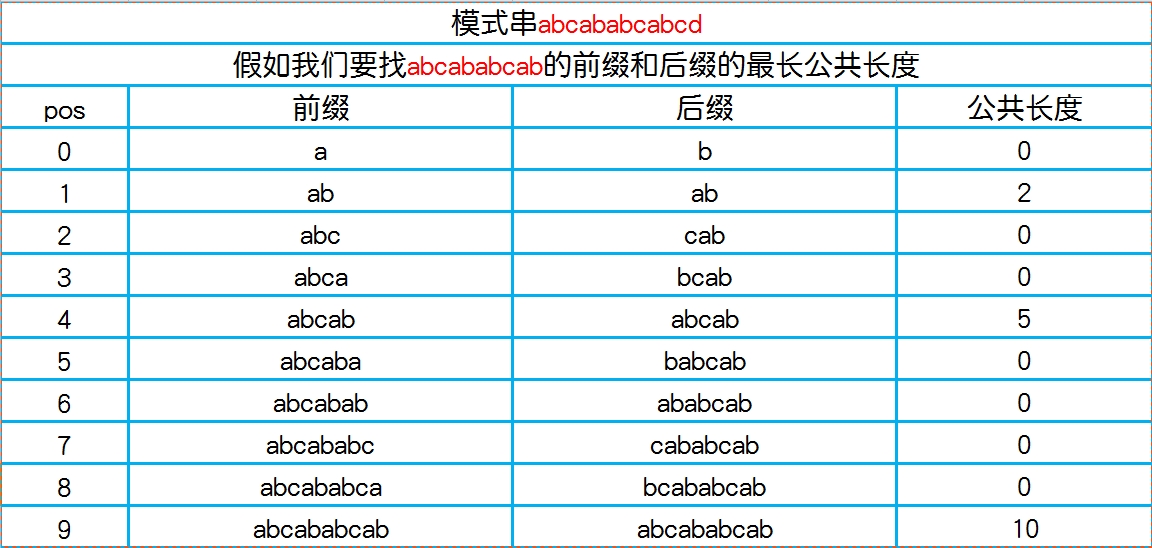
从这个表我们可以很清楚看到,所谓的前缀和后缀其实就是在第i个位置从前往后数和从pos位置从后往前数的一样的子串的长度
实现理论
-
构建next数组
-
模式串与目标串进行匹配,假设现在模式串和目标串已经匹配到j和i,那么
如果target[i]==text[j],则i++,j++(这个和暴力算法一致)
如果target[i]!=text[j],则使j通过next数组跳转到前一个j(假设是k位置,的相当于是使j匹配从pos向前移动pos-j个位置,再判断target[i]是否等于text[k],否则继续执行k=next[k],直到target[i]==text[k],如果无法找到合适的元素使target[i]==text[k],则另k=0,且i++
可以看到next数组是用来解决暴力解法的当匹配失败时就要j=0的缺点,可以让j跳转到某个合适的位置,继续匹配
当然了这个位置也不是随便乱选的,而这个位置就是刚好是当前元素前面元素的前缀后缀最长公共长度的后一个位置,当然了我们要要从当前位置跳转,我们关注的是当前位置前面的元素的情况,所以我们把上面那个表所有值往前移动一个单位,然后把0位置设置成-1就得到了next表了
模式串移动的原理
大家看到这里可能会很疑惑,究竟为什么跳转到前面元素的前缀和后缀最长公共的后一个位置前面一个位置就是可以的呢?这个的确不太好说明,我们只从例子上说明问题,我们先来举一个例子

从面例子中,其实移动到前注意和后缀最长公共位置是合理的,因为我们前后缀是相等的,我们移动后可以保证当前元素前面的元素都是匹配的,比如图中这个例子,移动以后AC还是和前面配过的元素一样,最后完成匹配,最后当然了,如果移动后还失配,还是需要相同的移动方法。直到移动到模式串的最前端为止(移动到最前端说明已经找不到任何匹配的元素了,相当于重新匹配模式串了)






