【12月DW打卡】joyful-pandas - 07 - pandas缺失数据 （缺失值的统计删除、填充插值、KNN的简单使用） + 脑图大纲

缺失数据

脑图大纲

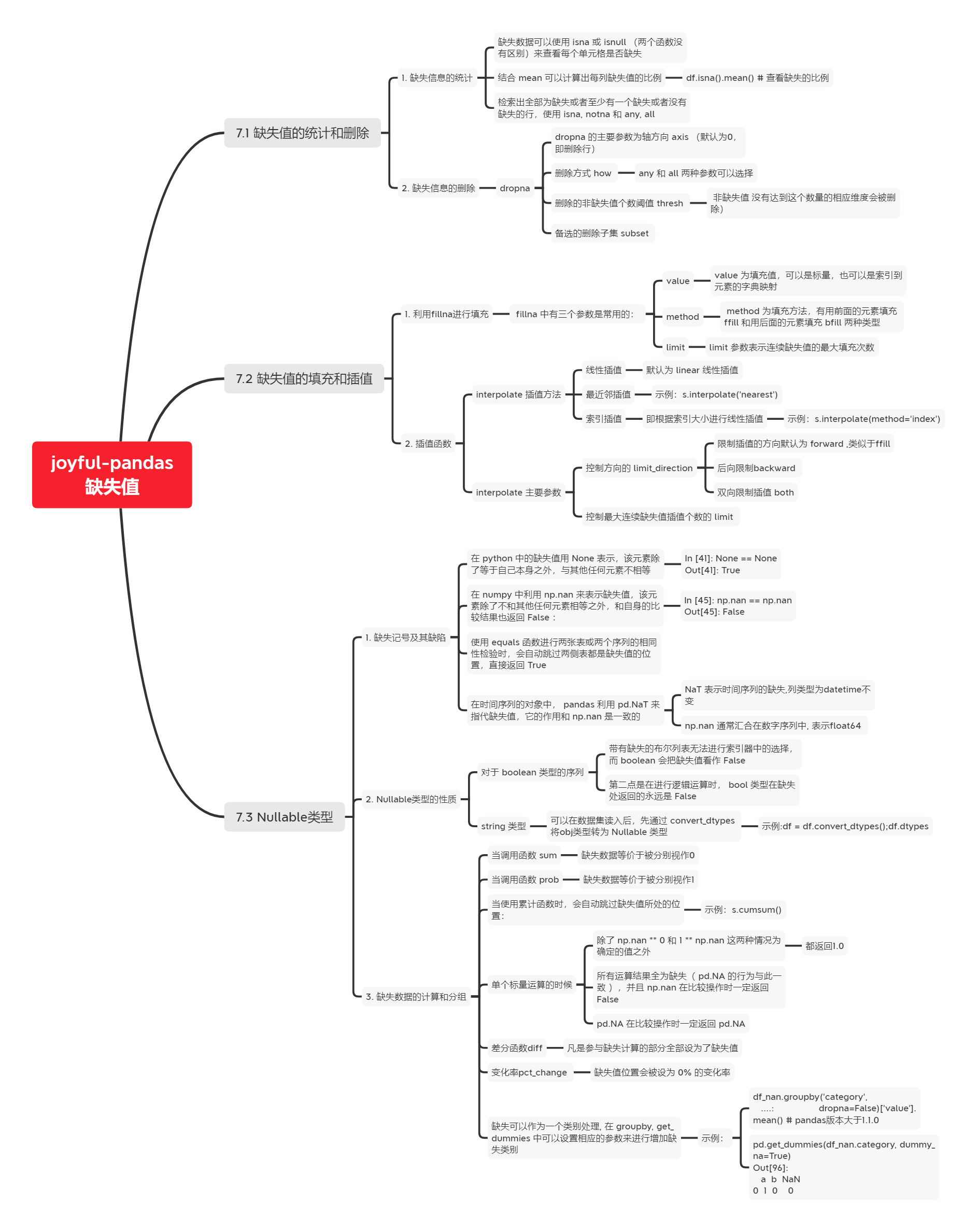
小结

import numpy as np
import pandas as pd

【7.2.1 练一练】

对一个序列以如下规则填充缺失值：如果单独出现的缺失值，就用前后均值填充，如果连续出现的缺失值就不填充，即序列[1, NaN, 3, NaN, NaN]填充后为[1, 2, 3, NaN, NaN]，请利用 fillna 函数实现。（提示：利用 limit 参数）

s = pd.Series([1, np.nan, 3, np.nan, np.nan],
              list('abcde'))

# s.fillna(method='both', limit=1) 不支持

ValueError: Invalid fill method. Expecting pad (ffill) or backfill (bfill). Got both

(s.fillna(method='ffill', limit=1) + s.fillna(method='bfill', limit=1))/2


a    1.0
b    2.0
c    3.0
d    NaN
e    NaN
dtype: float64

# 类似的interpolate方法,向后也是不可以的!
s.interpolate(limit_direction='both', limit=1)


a    1.0
b    2.0
c    3.0
d    3.0
e    NaN
dtype: float64

Ex1：缺失值与类别的相关性检验

在数据处理中，含有过多缺失值的列往往会被删除，除非缺失情况与标签强相关。下面有一份关于二分类问题的数据集，其中 X_1, X_2 为特征变量， y 为二分类标签。

df = pd.read_csv('E:\\PycharmProjects\\DatawhaleChina\\joyful-pandas\\data\\missing_chi.csv')

df.head()
X_1 X_2 y
0 NaN NaN 0
1 NaN NaN 0
2 NaN NaN 0
3 43.0 NaN 0
4 NaN NaN 0 
df.isna().mean()

X_1    0.855
X_2    0.894
y      0.000
dtype: float64

df.y.value_counts(normalize=True)


0    918
1     82
Name: y, dtype: int64

事实上，有时缺失值出现或者不出现本身就是一种特征，并且在一些场合下可能与标签的正负是相关的。关于缺失出现与否和标签的正负性，在统计学中可以利用卡方检验来断言它们是否存在相关性。按照特征缺失的正例、特征缺失的负例、特征不缺失的正例、特征不缺失的负例，可以分为四种情况，设它们分别对应的样例数为\(n_{11}, n_{10}, n_{01}, n_{00}\)。假若它们是不相关的，那么特征缺失中正例的理论值，就应该接近于特征缺失总数\(\times\)总体正例的比例，即：

\[E_{11} = n_{11} \approx (n_{11}+n_{10})\times\frac{n_{11}+n_{01}}{n_{11}+n_{10}+n_{01}+n_{00}} = F_{11} \]

其他的三种情况同理。现将实际值和理论值分别记作\(E_{ij}, F_{ij}\)，那么希望下面的统计量越小越好，即代表实际值接近不相关情况的理论值：

\[S = \sum_{i\in \{0,1\}}\sum_{j\in \{0,1\}} \frac{(E_{ij}-F_{ij})^2}{F_{ij}} \]

可以证明上面的统计量近似服从自由度为\(1\)的卡方分布，即\(S\overset{\cdot}{\sim} \chi^2(1)\)。因此，可通过计算\(P(\chi^2(1)>S)\)的概率来进行相关性的判别，一般认为当此概率小于\(0.05\)时缺失情况与标签正负存在相关关系，即不相关条件下的理论值与实际值相差较大。

上面所说的概率即为统计学上关于\(2\times2\)列联表检验问题的\(p\)值， 它可以通过scipy.stats.chi2(S, 1)得到。请根据上面的材料，分别对X_1, X_2列进行检验。

"""
2×2 列联表检验问题的 p 值:
特征缺失的正例  1
特征缺失的负例  0
特征不缺失的正例 1
特征不缺失的负例 0
"""

df = pd.read_csv('E:\\PycharmProjects\\DatawhaleChina\\joyful-pandas\\data\\missing_chi.csv')
# where 和 mask ，这两个函数是完全对称的： where 函数在传入条件为 False 的对应行进行替换，而 mask 在传入条件为 True 的对应行进行替换，当不指定替换值时，替换为缺失值。"
cat_1 = df.X_1.fillna('NaN').mask(df.X_1.notna(), "NotNaN")
cat_2 = df.X_2.fillna('NaN').mask(df.X_2.notna(), "NotNaN")
# pd.crosstab计算两个（或多个）因子的简单交叉表。默认情况下，除非传递值数组和聚合函数，否则将计算因子的频率表。
df_1 = pd.crosstab(cat_1, df.y, margins=True)
df_2 = pd.crosstab(cat_2, df.y, margins=True)
# 计算大S值
def compute_S(my_df):
    S = []
    for i in range(2):
        for j in range(2):
            E = my_df.iat[i, j]
            F = my_df.iat[i, 2]*my_df.iat[2, j]/my_df.iat[2,2]
            S.append((E-F)**2/F)
    return sum(S)
# 分别计算
res1 = compute_S(df_1)
res2 = compute_S(df_2)

0.9712760884395901

from scipy.stats import chi2
chi2.sf(res1, 1) # X_1检验的p值 # 不能认为相关，剔除

0.9712760884395901

chi2.sf(res2, 1) # X_2检验的p值 # 认为相关，保留(为当此概率小于0.05即符合条件)

7.459641265637543e-166

结果与scipy.stats.chi2_contingency在不使用\(Yates\)修正的情况下完全一致：

# 列联表中变量独立性的卡方检验。
from scipy.stats import chi2_contingency
chi2_contingency(pd.crosstab(cat_1, df.y), correction=False)[1]

0.9712760884395901

chi2_contingency(pd.crosstab(cat_2, df.y), correction=False)[1]



7.459641265637543e-166

Ex2：用回归模型解决分类问题

KNN是一种监督式学习模型，既可以解决回归问题，又可以解决分类问题。对于分类变量，利用KNN分类模型可以实现其缺失值的插补，思路是度量缺失样本的特征与所有其他样本特征的距离，当给定了模型参数n_neighbors=n时，计算离该样本距离最近的\(n\)个样本点中最多的那个类别，并把这个类别作为该样本的缺失预测类别，具体如下图所示，未知的类别被预测为黄色：

上面有色点的特征数据提供如下：

df = pd.read_excel('E:\\PycharmProjects\\DatawhaleChina\\joyful-pandas\\data\\color.xlsx')
df.head(3)
X1 X2 Color
0 -2.5 2.8 Blue
1 -1.5 1.8 Blue
2 -0.8 2.8 Blue

已知待预测的样本点为\(X_1=0.8, X_2=-0.2\)，那么预测类别可以如下写出：

from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=6)
clf.fit(df.iloc[:,:2], df.Color)
clf.predict([[0.8, -0.2]])

array(['Yellow'], dtype=object)
  1. 对于回归问题而言，需要得到的是一个具体的数值，因此预测值由最近的\(n\)个样本对应的平均值获得。请把上面的这个分类问题转化为回归问题，仅使用KNeighborsRegressor来完成上述的KNeighborsClassifier功能。

翻到源码的Examples

    --------
    >>> X = [[0], [1], [2], [3]]
    >>> y = [0, 0, 1, 1]
    >>> from sklearn.neighbors import KNeighborsRegressor
    >>> neigh = KNeighborsRegressor(n_neighbors=2)
    >>> neigh.fit(X, y)
    KNeighborsRegressor(...)
    >>> print(neigh.predict([[1.5]]))
    [0.5]

照葫芦画瓢~~~

df_dummies = pd.get_dummies(df.Color)
df_dummies.head()

from sklearn.neighbors import KNeighborsRegressor
X = df[['X1', 'X2']]
# y = [0, 0, 1, 1]
stack_list = []
for col in df_dummies.columns:
    print(col)
    neigh = KNeighborsRegressor(n_neighbors=6)
    neigh.fit(X, df_dummies[col])
    # 转为单列数据
    res = neigh.predict([[0.8, -0.2]]).reshape(-1,1)
    print(neigh.predict([[0.8, -0.2]]))
    stack_list.append(res)
stack_list

Blue
[0.16666667]
Green
[0.33333333]
Yellow
[0.5]





[array([[0.16666667]]), array([[0.33333333]]), array([[0.5]])]

由上可知: 预测成蓝/绿/黄三个颜色的概率分别是0.16666667，33.3%和50%。
取最大的概率作为最终预测结果，该位置最终预测为黄色。

# np.hstack : 水平（按列）顺序堆叠数组。 [这里返回一个单列数组]
# argmax : Return indices of the maximum values along the given axis.
color_res = pd.Series(np.hstack(stack_list).argmax(axis=1))
df_dummies.columns[color_res[0]]
# 输出为'Yellow'

'Yellow'
  1. 请根据第1问中的方法，对audit数据集中的Employment变量进行缺失值插补。
df = pd.read_csv('E:\\PycharmProjects\\DatawhaleChina\\joyful-pandas\\data\\audit.csv')
df.head(3)

from sklearn.neighbors import KNeighborsRegressor

# df = pd.read_csv('data/audit.csv')

res_df = df.copy()

#将婚姻状况、性别变成one-hot向量，和年龄、收入、时间、雇用拼接在一起
# 年龄、收入、时间这三个属性还做了标准化处理
df = pd.concat([pd.get_dummies(df[['Marital', 'Gender']]),
        df[['Age','Income','Hours']].apply(
            lambda x:(x-x.min())/(x.max()-x.min())), df.Employment],1)


X_train = df[df.Employment.notna()]

X_test = df[df.Employment.isna()]



df_dummies = pd.get_dummies(X_train.Employment)

stack_list = []

for col in df_dummies.columns:
        clf = KNeighborsRegressor(n_neighbors=6)
        clf.fit(X_train.iloc[:,:-1], df_dummies[col])
        res = clf.predict(X_test.iloc[:,:-1]).reshape(-1,1)
        stack_list.append(res)

code_res = pd.Series(np.hstack(stack_list).argmax(1))

code_res


0     2
1     0
2     4
3     4
4     4
     ..
95    4
96    4
97    4
98    4
99    4
Length: 100, dtype: int64

cat_res = code_res.replace(
    dict(
    zip(list(range(df_dummies.shape[0])), df_dummies.columns))
)

res_df.loc[res_df.Employment.isna(), 'Employment'] = cat_res.values

res_df.isna().sum()

ID            0
Age           0
Employment    0
Marital       0
Income        0
Gender        0
Hours         0
dtype: int64
posted @ 2021-01-03 23:30  山枫叶纷飞  阅读(346)  评论(0)  编辑  收藏  举报