初学推荐系统-06- GBDT+LR模型

1. GBDT+LR简介

协同过滤+矩阵分解：仅仅利用了用户与物品相互行为信息进行推荐， 忽视了用户自身特征，物品自身特征以及上下文信息等，导致生成的结果往往会比较片面。
Facebook提出的GBDT+LR模型：GBDT自动进行特征筛选和组合，进而生成新的离散特征向量，再把该特征向量当做LR模型的输入，来产生最后的预测结果。在CTR点击率预估的场景下使用较为广泛。

2. LR（逻辑回归模型）

逻辑回归在线性回归的基础上加了一个Sigmod函数（非线性）映射，使得逻辑回归成为了一个优秀的布尔分类算法，学习逻辑回归模型，首先要记得一句话：逻辑回归假设数据服从伯努利分布，再通过极大化似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。
逻辑回归模型将推荐问题转化成了一个点击率预估问题，而点击率预测就是一个典型的二分类。
LR的推荐过程：
- 1. 将用户年龄、性别、物品属性、物品描述、当前时间、当前地点等特征转成数值型向量
- 1. 确定逻辑回归的优化目标，比如把点击率预测转换成二分类问题，这样就可以得到分类问题常用的损失作为目标，训练模型
- 1. 在预测的时候，将特征向量输入模型产生预测，得到用户“点击”物品的概率
- 1. 利用点击概率对候选物品排序，得到推荐列表
    推断过程可以用下图来表示：
LR的优点
- 逻辑回归模型简单,可解释性好,从特征的权重可以看到不同特征对最后的结果的影响.
- 训练时便于并行化，在预测时只需要对特征进行线性加权，所以性能较好；往往适合处理海量id类特征，用id类特征有一个很重要的好处，就是防止信息损失（相对于范化的 CTR 特征），对于头部资源会有更细致的描述。
- 资源占用小,尤其是内存。在实际的工程应用中只需要存储权重比较大的特征及特征对应的权重。
- 方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果，因为输出的是每个样本的概率分数，我们可以很容易的对这些概率分数进行cutoff，也就是划分阈值(大于某个阈值的是一类，小于某个阈值的是一类)
LR的缺点
- 表达能力不强，无法进行特征交叉，特征筛选能一些列的高级操作；因为很容易造成信息的损失——也就是误删，往往需要人工进行干预。
- 准确率不是很高，因为这毕竟是一个线性模型加了一个sigmod函数，形式十分简单，非常类似线性模型，很难拟合真实数据的真实分布。
- 处理非线性数据较为麻烦，逻辑回归在不引入其他方法的情况下，只能处理线性可分的模型；连续性数据需要进行分桶，进行离散化操作。
- LR需要进行人工特征的组合，这就需要开发者有非常丰富的领域经验，这样的模型迁移起来比较困难，换一个领域又需要重新进行大量的特征工程。
  所以，如何进行发现有效的特征、特征组合，十分重要。而GBDT模型，正好可以自动发现特征并进行有效地组合。

3. GBDT模型

GBDT全称梯度提升决策树，通过采用加法模型(及不同基模型的线性组合、加权得到总回归器)、以及不断地减少训练过程中产生的误差来达到数据分类或者回归的算法，多训练器组合如下：

4. GBDT+LR模型

2014年， Facebook提出了一种利用GBDT自动进行特征筛选和组合，进而生成新的离散特征向量，再把该特征向量当做LR模型的输入，来产生最后的预测结果，这就是著名的GBDT+LR模型了。GBDT+LR 使用最广泛的场景是CTR点击率预估，即预测当给用户推送的广告会不会被用户点击。

有了上面的铺垫，这个模型解释起来就比较容易了，模型的总体结构长下面这样：
在这里插入图片描述

训练时

GBDT 建树的过程相当于自动进行的特征组合和离散化，然后从根结点到叶子节点的这条路径就可以看成是不同特征进行的特征组合，用叶子节点可以唯一的表示这条路径，并作为一个离散特征传入 LR 进行二次训练。

比如上图中，有两棵树，x为一条输入样本，遍历两棵树后，x样本分别落到两颗树的叶子节点上，每个叶子节点对应LR一维特征，那么通过遍历树，就得到了该样本对应的所有LR特征。构造的新特征向量是取值0/1的。比如左树有三个叶子节点，右树有两个叶子节点，最终的特征即为五维的向量。对于输入x，假设他落在左树第二个节点，编码[0,1,0]，落在右树第二个节点则编码[0,1]，所以整体的编码为[0,1,0,0,1]，这类编码作为特征，输入到线性分类模型（LR or FM）中进行分类。

预测时

会先走 GBDT 的每棵树，得到某个叶子节点对应的一个离散特征(即一组特征组合)，然后把该特征以 one-hot 形式传入 LR 进行线性加权预测。

这个方案应该比较简单了，下面有几个关键的点我们需要了解：

通过GBDT进行特征组合之后得到的离散向量是和训练数据的原特征一块作为逻辑回归的输入，而不仅仅全是这种离散特征
建树的时候用ensemble建树的原因就是一棵树的表达能力很弱，不足以表达多个有区分性的特征组合，多棵树的表达能力更强一些。GBDT每棵树都在学习前面棵树尚存的不足，迭代多少次就会生成多少棵树。
RF也是多棵树，但从效果上有实践证明不如GBDT。且GBDT前面的树，特征分裂主要体现对多数样本有区分度的特征；后面的树，主要体现的是经过前N颗树，残差仍然较大的少数样本。优先选用在整体上有区分度的特征，再选用针对少数样本有区分度的特征，思路更加合理，这应该也是用GBDT的原因。
在CRT预估中， GBDT一般会建立两类树(非ID特征建一类， ID类特征建一类)， AD，ID类特征在CTR预估中是非常重要的特征，直接将AD，ID作为feature进行建树不可行，故考虑为每个AD，ID建GBDT树。
1. 非ID类树：不以细粒度的ID建树，此类树作为base，即便曝光少的广告、广告主，仍可以通过此类树得到有区分性的特征、特征组合
2. ID类树：以细粒度的ID建一类树，用于发现曝光充分的ID对应有区分性的特征、特征组合

5. 编程实践

下面我们通过kaggle上的一个ctr预测的比赛来看一下GBDT+LR模型部分的编程实践，数据来源

我们回顾一下上面的模型架构，首先是要训练GBDT模型， GBDT的实现一般可以使用xgboost，或者lightgbm。训练完了GBDT模型之后，我们需要预测出每个样本落在了哪棵树上的哪个节点上，然后通过one-hot就会得到一些新的离散特征，这和原来的特征进行合并组成新的数据集，然后作为逻辑回归的输入，最后通过逻辑回归模型得到结果。

根据上面的步骤，我们看看代码如何实现：

假设我们已经有了处理好的数据x_train, y_train:

### LR + GBDT建模
下面就是把上面两个模型进行组合， GBDT负责对各个特征进行交叉和组合， 把原始特征向量转换为新的离散型特征向量， 然后再使用逻辑回归模型

#%%

def gbdt_lr_model(data, category_feature, continuous_feature): # 0.43616
    # 离散特征one-hot编码
    for col in category_feature:
        onehot_feats = pd.get_dummies(data[col], prefix = col)
        data.drop([col], axis = 1, inplace = True)
        data = pd.concat([data, onehot_feats], axis = 1)

    train = data[data['Label'] != -1]
    target = train.pop('Label')
    test = data[data['Label'] == -1]
    test.drop(['Label'], axis = 1, inplace = True)

    # 划分数据集
    x_train, x_val, y_train, y_val = train_test_split(train, target, test_size = 0.2, random_state = 2020)

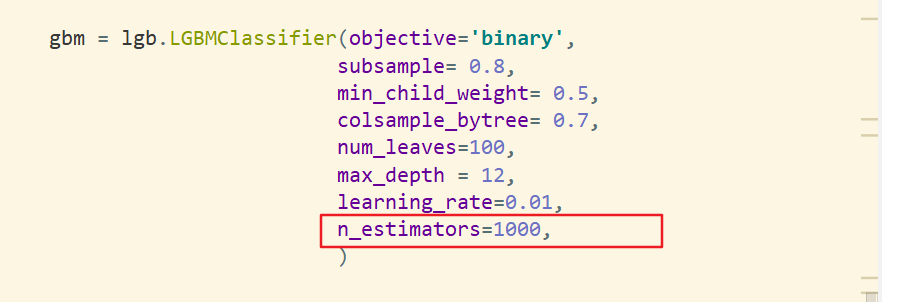
    gbm = lgb.LGBMClassifier(objective='binary',
                            subsample= 0.8,
                            min_child_weight= 0.5,
                            colsample_bytree= 0.7,
                            num_leaves=100,
                            max_depth = 12,
                            learning_rate=0.01,
                            n_estimators=1000,
                            )

    gbm.fit(x_train, y_train,
            eval_set = [(x_train, y_train), (x_val, y_val)],
            eval_names = ['train', 'val'],
            eval_metric = 'binary_logloss',
            early_stopping_rounds = 100,
            )
    
    model = gbm.booster_

    gbdt_feats_train = model.predict(train, pred_leaf = True)
    gbdt_feats_test = model.predict(test, pred_leaf = True)
    gbdt_feats_name = ['gbdt_leaf_' + str(i) for i in range(gbdt_feats_train.shape[1])]
    df_train_gbdt_feats = pd.DataFrame(gbdt_feats_train, columns = gbdt_feats_name) 
    df_test_gbdt_feats = pd.DataFrame(gbdt_feats_test, columns = gbdt_feats_name)

    train = pd.concat([train, df_train_gbdt_feats], axis = 1)
    test = pd.concat([test, df_test_gbdt_feats], axis = 1)
    train_len = train.shape[0]
    data = pd.concat([train, test])
    del train
    del test
    gc.collect()

    # # 连续特征归一化
    scaler = MinMaxScaler()
    for col in continuous_feature:
        data[col] = scaler.fit_transform(data[col].values.reshape(-1, 1))

    for col in gbdt_feats_name:
        onehot_feats = pd.get_dummies(data[col], prefix = col)
        data.drop([col], axis = 1, inplace = True)
        data = pd.concat([data, onehot_feats], axis = 1)

    train = data[: train_len]
    test = data[train_len:]
    del data
    gc.collect()

    x_train, x_val, y_train, y_val = train_test_split(train, target, test_size = 0.3, random_state = 2020)

    
    lr = LogisticRegression()
    lr.fit(x_train, y_train)
    tr_logloss = log_loss(y_train, lr.predict_proba(x_train)[:, 1])
    print('tr-logloss: ', tr_logloss)
    val_logloss = log_loss(y_val, lr.predict_proba(x_val)[:, 1])
    print('val-logloss: ', val_logloss)
    y_pred = lr.predict_proba(test)[:, 1]
    print(y_pred[:10])

#%%

# 训练和预测
gbdt_lr_model(data.copy(), category_fea, continuous_fea)

输出打印:

...
[238]	train's binary_logloss: 0.274511	val's binary_logloss: 0.438652
[239]	train's binary_logloss: 0.273894	val's binary_logloss: 0.438641
[240]	train's binary_logloss: 0.273434	val's binary_logloss: 0.438684
Early stopping, best iteration is:
[140]	train's binary_logloss: 0.337805	val's binary_logloss: 0.435102
tr-logloss:  0.01253347064922472
val-logloss:  0.31119462612062593
[9.79618677e-01 3.56919973e-01 4.69387468e-02 1.14859507e-02
 1.05509467e-02 6.39457799e-01 5.40628075e-02 2.85946933e-03
 9.39182398e-04 3.65430285e-01]

6. 课后思考

为什么要使用集成的决策树？而不使用单棵的决策树模型~

一棵树的表达能力有限，不足以表达多个有区别性的特征组合，多棵树的表达能力会更强一些；可以更好地发现有效的特征以及特征组合。

** 为什么使用GBDT构建决策树而不是随机森林？**

随机森林是由很多决策树构成的，不同决策树之间没有关联。
GBDT构建决策树，可以更好地发现有效的特征以及特征组合；GBDT前面的树，特征分裂主要体现在对多数样本有区分度的特征，后面的树，主要体现在经过前N棵树处理后--残差仍然比较大的少数样本；GBDT优先选用在整体上有区分度的特征，再选择针对少数样本有区分度的特征，思路更加合理，这应该是用GBDT的原因。

面对高维稀疏类特征的时候(比如ID类特征)， LR逻辑回归一般要比GBDT这种非线性模型好，为什么？

面对高维稀疏类特征的时候，带正则化的线性模型比较不容易对稀疏特征过拟合。
LR(y=w1f1+w2f2+...)中，若w1特别大，惩罚也会很大，进一步压缩W1的值，使它不至于过大；
而树模型则不一样，树模型的惩罚项通常为叶子结点树和树深度来作为惩罚项；举例10k的样本中-9.99k的样本的f1属性为0、其余0.01k的f1属性都为1，树模型只需要一个结点就可以完美分割9.99k和10个的样本,惩罚项极其之小.

7. 参考资料

论文

posted @ 2020-10-30 22:19 山枫叶纷飞阅读(936) 评论(0) 编辑收藏举报

刷新页面返回顶部

好好学习，天天向上

啦啦啦啦，一起来自学打卡，冲冲冲~