时序预测 04 - Prophet的拓展 傅里叶级数与《傅里叶分析之掐死教程》 - 数学公式（挖个坑，待填）

引用

如何理解傅立叶级数公式？https://www.matongxue.com/madocs/619 知 乎：马同学
如何通俗地理解傅立叶变换？https://www.matongxue.com/madocs/473 知 乎：马同学
傅里叶分析之掐死教程（完整版） https://zhuanlan.zhihu.com/p/19763358 知 乎：Heinrich
百科 频域 https://baike.baidu.com/item/频域
B站的李永乐老师的账号下也有相关教学视频内容，十分生动形象，可以参考

Prophet与傅里叶的关联、参数影响

01 在Prophet对象中添加季节性组件的时候


翻译一下:

Increasing the number of Fourier components allows the seasonality to
        change more quickly (at risk of overfitting). Default values for yearly
        and weekly seasonalities are 10 and 3 respectively.

内容为:

增加傅里叶分量的数量允许季节性变换得更快（有过拟合的风险）。
年度和每周季节性的默认值分别为10和3。

个人的附加解释: 增加傅里叶分量,可以增加更多的傅里叶函数进行拟合,拟合的效果会得到增加.

后续，发现更多的关联再进行补充。

傅里叶分析之掐死教程（完整版） 等 速读笔记

知乎 https://zhuanlan.zhihu.com/p/19763358
ps 文章的目的是： 要让读者在不看任何数学公式的情况下理解傅里叶分析。（所以缺少数学证明）

零、什么是傅里叶变换

傅里叶变换，表示可以将满足一定条件的某个函数表示为正余弦函数（和、或）、或者它们积分的线性组合。

一、什么是时域、频域

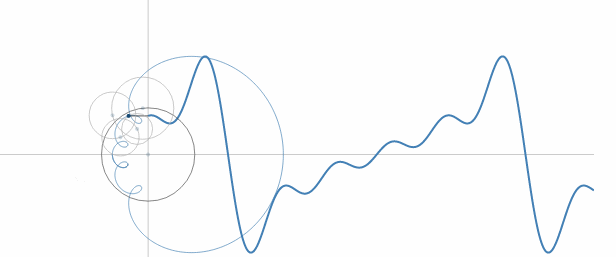
时域： 以时间为参考来观察动态世界的方法，我们称之为时域分析；（旋转与傅立叶级数）

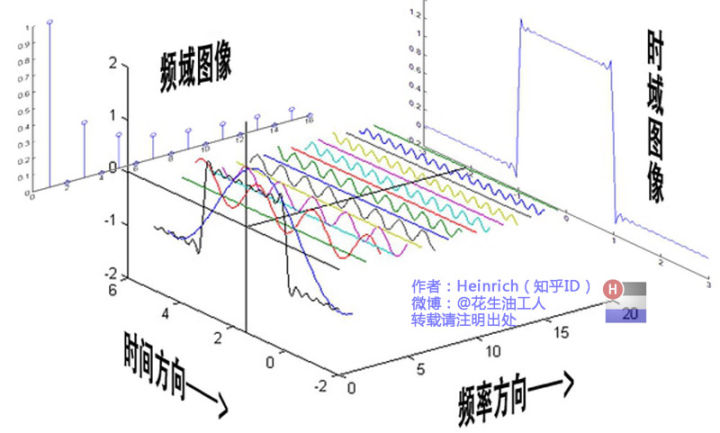
频域： 频域图显示了在一个频率范围内多个给定频率的最大信号量在平面上的投影图像，简言之————多个频率的单位时间内的信号量值的投影集合 (线性代数与傅立叶级数)

对于：

我们用(n,c_n)来描点作图，就得到频谱图。

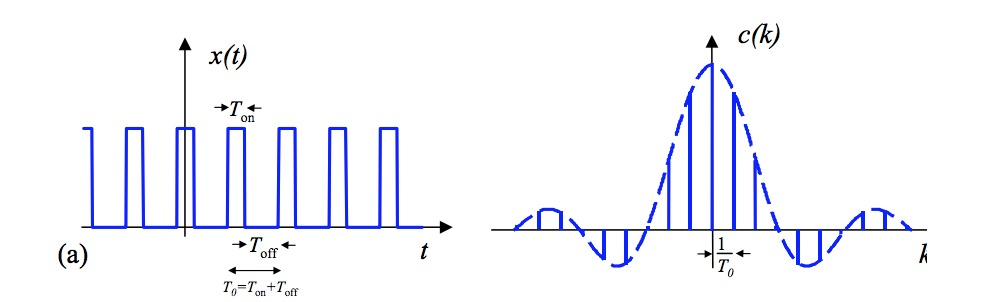
二、傅里叶级数(Fourier Series)的频谱

python 代码简单打印:

    x = np.linspace(0,10,1000)
    y = 4*np.sin(x)/math.pi +  4*np.sin(3*x)/math.pi/3 \
        +  4*np.sin(5*x)/math.pi/5
    print('------------')
    plt.figure()
    plt.plot(x,y)
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文标签
    plt.rcParams['axes.unicode_minus'] = False
    plt.title('傅里叶变换波形')
    plt.show()

效果:

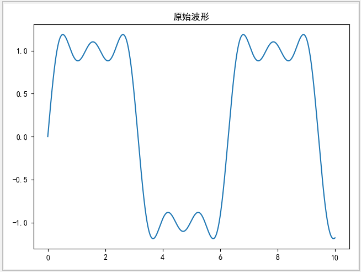
小结: 经过多次叠加, 正弦波就是一个圆周运动在一条直线上的运动;所以频域的一个基本单元就是可以理解为一个始终在旋转的圆(多个圆之间可以互相嵌套~)

三、傅里叶级数（Fourier Series）的相位谱

(当信号波形以周期的方式变化，波形循环一周即为360° ——2*Pi)
时间差: 距离频率轴最近的波峰在x轴上的投影值
相位差: 将时间差除周期再乘 2Pi
正弦函数的相位: 即将离频率轴最近的波峰向左平移到波峰和频率轴重合的距离

四、傅里叶变换（Fourier Transformation）

傅里叶级数 的本质是将一个周期的信号分解成无限多分开的（离散的）正弦函数波.

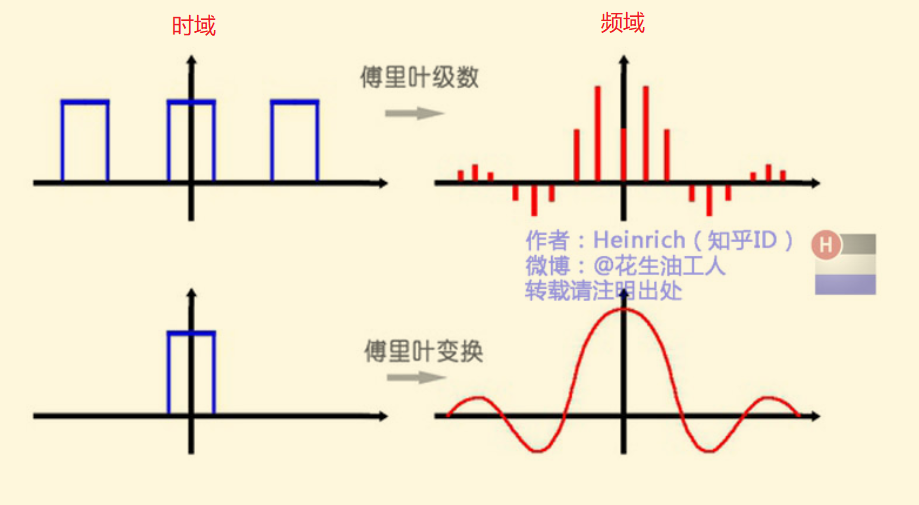
傅里叶变换 实际上就是对一个周期无限大的函数使用傅里叶级数代表的函数来拟合

离散谱（相加）转换为连续谱（积分）

图略

五. 欧拉公式 (具体推导公式见笔记本)

虚数i: ** 这个概念大家在高中就接触过，但那时我们只知道它是-1的平方根**
欧拉公式

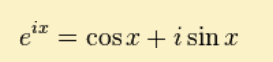
当x等于Pi时, 可以推出

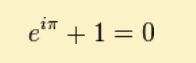
这个公式关键的作用，是将正弦波统一成了简单的指数形式,图像上的涵义：

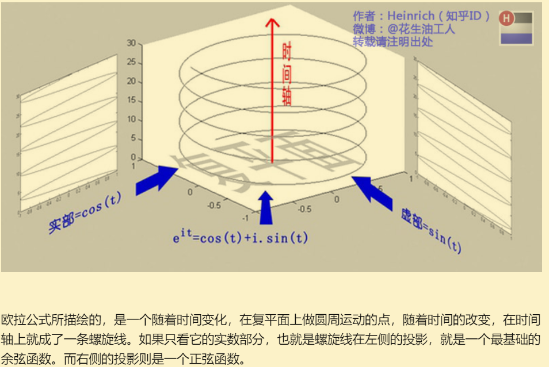
欧拉公式所描绘的，是一个随着时间变化，在复平面上做圆周运动的点，随着时间的改变，在时间轴上就成了一条螺旋线。
如果只看它的实数部分，也就是螺旋线在左侧的投影，就是一个最基础的余弦函数。而右侧的投影则是一个正弦函数。

六、指数形式的傅里叶变换

我们可以用两种方法来理解正弦波：

图形化总结:

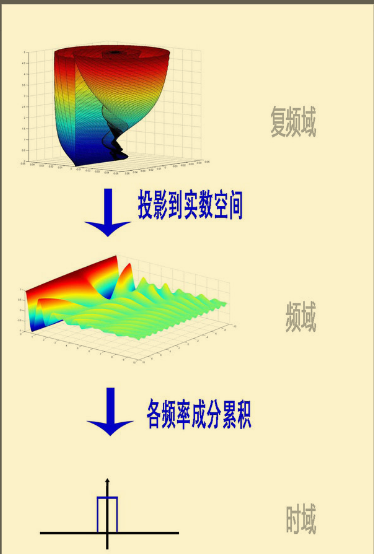
七、傅里叶级数的常见应用场景 （注：理想的傅立叶分析针对的是封闭、线性、时不变系统）

https://www.zhihu.com/search?q=傅里叶变换的应用&utm_content=search_suggestion&type=content

  • 比如音频和视频处理，首先人耳的耳蜗就是识别频率的幅度信息的
  • 图像处理，比如最常见的图像压缩
  • 通讯系统领域，对于现代通信的几乎每一个概念，傅立叶变换都是基础中的基础。
  • 预测：算了，放弃

八、傅里叶变换的数学公式证明原理 TODO

如何理解傅立叶级数公式？https://www.matongxue.com/madocs/619 知 乎：马同学
如何通俗地理解傅立叶变换？https://www.matongxue.com/madocs/473 知 乎：马同学
挖个坑,待填

posted @ 2020-10-09 23:30  山枫叶纷飞  阅读(1171)  评论(0)  编辑  收藏  举报