《机器学习》笔记 第2章——模型评估与选择: 经验误差与过拟合、评估方法、性能度量、比较检验方法、偏差与方差
2.1 经验误差与过拟合
- 错误率: E = a(错误数) / m(样本数)
- 精度 = 1 - 错误率
- 误差: 在训练集上的误差成为训练误差,在新样本上的误差成为泛化误差
- NP问题: NP完全问题,即多项式复杂程度的非确定性问题。简单的写法是 NP=P?, 特征:求解困难程度远高于验证的困难程度,如素数
- NPC问题: NP通过一个多项式时间算法转换为某个NP问题, 该NP问题也可以称为NP完全问题
- “千僖难题”之一:P (确定性多项式算法)对NP (非确定性多项式算法)
- 搜索办法:
- 近邻法:
- 插入法:
- 模拟退火算法: 模拟退火算法与初始值无关,算法求得的解与初始解状态S(是算法迭代的起点)无关;模拟退火算法具有渐近收敛性,已在理论上被证明是一种以概率l 收敛于全局最优解的全局优化算法;模拟退火算法具有并行性。
- 遗传算法: 由基本的操作算子: 选择、杂交、变异构成, 是一类借鉴生物界的进化规律设计的算法
- 神经网络算法:
2.2 评估方法
- 留出法 hold-out
- 将数据集D划分为两个互斥的集合 S和T, 在S上训练得出的模型在T上进行评测
- 注意数据分布的一致性, 避免数据划分过程引入额外的偏差而对最终结果产生影响
- 从采样(sampling)角度来看, S和T中的正反例分布要保持相等,
- 分层采样: 即是保留类别比例的采样方式
- 一般采用: 若干次随机划分/重复进行试验求平均值作为留出法的评估结果
- 交叉验证法 cross validation
- K折交叉验证: 随机使用不同的划分方法重复P次, 最终取均值; 例如:
10次的0折交叉验证
- K折交叉验证: 随机使用不同的划分方法重复P次, 最终取均值; 例如:
- 留一法 (LOO方法)
- 设数据集大小为n, 令k=n, 即N折交叉验证, n-1:1 的比例进行训练模型, 训练n-1次, 得出n-1个模型
- 更准确: 只比原始数据集少了一个数据
- 开销昂贵, 比如数据规模达到百万级别, +调参的耗费
没有免费的午餐, 大量的噪点也加入了进来
- 自助法(bootstrapping)
-
减少训练样本规模下降带来的整体差异
-
设总数据集合为D, 每次又放回抽取出1个,直至M个,m取极限值, 大概36.8%的数据抽取不到——这部分总是没有抽取到的数据作为训练集
极限公式为:
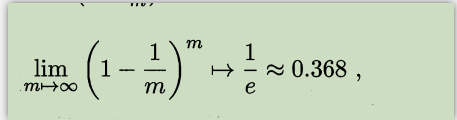
-
适用于: 数据集规模较小、难于有效划分训练集和测试集
-
- 调参与最终模型
- 验证集: 将训练集再分为训练集和验证集,验证效果较好后,再拿测试集得到输出结果
2.3 性能度量
- 均方误差 mean squared error (误差的平方的平均值)
- E = 1/m * sum(xi-yi) ^ 2;
- 错误率和精度
- 错误率计算: 分类错误的样本数站总样本数的比例
- 精度 = 1-错误率
- 查准率:正例->正例 / (正例->正例 + 反例->正例) 的比值
- 降低没有权重的样本数据的数量
- 查全率:正例->正例 / (正例->正例 + 正例->反例) 的比值
- 提升样本数据,提升查全率
- 查准率和查全率
- 往往互相矛盾
- ROC和AUC
- ROC曲线可以简单反应学习器泛化性能
- AUC : ROC曲线与x轴围成的面积
- 代价敏感错误率与代价曲线
- 代价敏感错误率:考虑不同的预测结果的后果
- 代价曲线(cost curse):
2.4 比较检验方法
- 假设检验
- t检验(t-test):假设我们得到了k个测试错误率
- 二项检验
- 交叉验证t检验
- 成对t检验(paired t-tests), 基本思想是,若两个学习的性能相同,则他们使用相同的训练、测试集得到的测试错误率应该相同
- 交叉验证t检验
- McNemar检验
- Friedman检验与Nenenyi后续检验
2.5 偏差与方差
- 偏差与方差
- 偏差-方差分解 (bias-variance decomposition) 解释学习算法 泛化性能 的一种重要工具
- 偏差:期望输出与真实标记的差别成为偏差
- 泛化误差:偏差、方差与噪声之和
- 偏差的意义:度量了学习算法的期望预测与真实结果的偏离程度,即可以刻画学习算法的本身的拟合能力
- 方差的意义:度量了同样大小的训练集的变动所导致学习性能(错误率和精度)的变化,即刻画了数据扰动带来的影响
- 噪声的意义:编导了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了学习问题本身的难度
- 总结:偏差-方差分解说明,泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所功能组成决定的
- 偏差-方差分解 (bias-variance decomposition) 解释学习算法 泛化性能 的一种重要工具
你不逼自己一把,你永远都不知道自己有多优秀!只有经历了一些事,你才会懂得好好珍惜眼前的时光!



