day1
day 1
雷暴 (storm)
题目要求计算覆盖所有相同颜色格子的最小正方形的面积。
#include <bits/stdc++.h>
using namespace std;
int n, m, k;
int a[1005][1005];
struct node{
int x, y;
}f[100005], g[100005];
int main()
{
freopen("storm.in", "r", stdin);
freopen("storm.out", "w", stdout);
ios :: sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> k;
for(int i = 1;i <= n;i++)
for(int j = 1;j <= m;j++)
cin >> a[i][j];
for(int i = 1;i <= n;i++)
for(int j = 1;j <= m;j++)
{
if(f[a[i][j]].x == 0 && f[a[i][j]].y == 0)
{
f[a[i][j]].x = i;
f[a[i][j]].y = j;
}
else
{
f[a[i][j]].x = min(f[a[i][j]].x, i);
f[a[i][j]].y = min(f[a[i][j]].y, j);
}
}
for(int i = 1;i <= n;i++)
for(int j = 1;j <= m;j++)
{
if(g[a[i][j]].x == 0 && g[a[i][j]].y == 0)
{
g[a[i][j]].x = i;
g[a[i][j]].y = j;
}
else
{
g[a[i][j]].x = max(g[a[i][j]].x, i);
g[a[i][j]].y = max(g[a[i][j]].y, j);
}
}
for(int i = 1;i <= k;i++)
{
int t = abs(max(g[i].x - f[i].x, g[i].y - f[i].y)) + 1;
cout<<t * t<<"\n";
}
return 0;
}
神力
小z初始在0号位置,每次都会向左或向右走一个单位坐标,他的行走轨迹可以看作一个长度为n的序列\(a_i\)保证\(abs\)|\(a_i\)| \(=1\)
因为神力的存在,所以小 Z 有\(\frac{p}{100}\)的概率可能在第 i 个时刻突然不想移动了,即不
进行这个时刻的移动操作
题目需要计算小Z经过各个位置的概率,并返回对应的结果。
样例
输入
5 83
1 -1 -1 1 1
输出
0 0 0 710859005 390982003 1 135049706 506522154 13802205 0 0
soluton
我们考虑从后往前,令\(f_i,_j\)考虑了后\(i\)步操作,当前位置为\(j\)的概率。
每次只要将\(f_i,0\)设为1即可
code
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 5005, MOD = 1e9 + 7;
int qpow(int x, int y)
{
int cnt = 1;
for(; y; y >>= 1)
{
if(y & 1) cnt = cnt * x % MOD;
x = x * x % MOD;
}
return cnt;
}
int n, p, a[N], dp[N][N * 2], ans;
signed main()
{
cin >> n >> p;
p = p * qpow(100, MOD - 2) % MOD;
int ip = (1 - p + MOD) % MOD;
for(int i = 1;i <= n;i++)
cin >> a[i];
dp[0][n] = 1;
for(int i = 1;i <= n;i++)
{
for(int j = n - i + 1;j <= n + i - 1;j++)
{
dp[i][j] = (dp[i][j] + p * dp[i - 1][j]) % MOD;
dp[i][j + a[n - i + 1]] = (dp[i][j + a[n - i + 1]] + ip * dp[i - 1][j]) % MOD;
}
dp[i][n] = 1;
}
for(int i = 0;i <= 2 * n;i++)
cout<<dp[n][i]<<" ";
cout<<"\n";
return 0;
}
之缘千里(fate)##
缘分化成了一个长度为 2n 的合法括号串,这 2n 个字符(( 或 ))代表了 2n 个灵
魂,分成 n 组命运,每组恰好包含 2 个灵魂。
对于每组灵魂,由于它们相互连接,所以它们代表的字符需要相同。
现在,给定这 2n 个灵魂所在的命运组,求是否存在这样的合法括号串,如果存在,
则构造一组字典序最小的解,否则输出 😦 表示不存在。
特别地,如果你构造的解不满足字典序最小,但也是合法括号串,你可以获得这个测试点 50% 的分数。
样例
输入
4
1 1 3 2 2 4 4 3
输出
(()(()))
solution
引理
一个长度为\(2n\)的括号串合法,当且仅当所有左括号的位置能被\(1, 3, 5, 7...,2n - 1\)偏序
证明
和括号前缀函数\(>0\)是等价的
算法
令\(nxt_i\)表示\(a_i\)右侧对应的位置
于是我们可以看作是左括号位置和\(1, 3, 5, 7...,2n - 1\)的位置匹配。
时间复杂度$O(n \(log\) n)
code
#include <bits/stdc++.h>
using namespace std;
#define F(i, j, k) for(int i = j;i <= k;i++>)
const intn N = 2e6 + 10;
int n, p[N], nxt[N], h[N], ans[N];
set<int> st;
int main()
{
cin >> n;
F(i, 1, n * 2)
{
cin >> p[i];
nxt[h[p[i]]] = i;
h[p[i]] = i;
}
F(i, 1, n)
st.insert(i * 2 - 1);
F(i, 1, n * 2)
if(nxt[i]){
if(st.size() && st.rbegin() >= nxt[i]){
st.erase(st.lower_bound(nxt[i]));
auto p = st.lower_bound(i);
if(p == st.end()) return puts(":("), 0;
st.erase(p), ans[i] = ans[nxt[i]] = 1;
}
}
if(st.size()) return puts(":("), 0;
F(i, 1, n * 2) cout<<(ans[i] ? '(' : ')');
return 0;
}
怒气冲天(rectangle)
给定\(n\)个矩形,求有几个三元组\((i, j, k)\), 满足\((i, j), (j, k), (i, k)\)没有交
solution
矩形满足以下四种情况
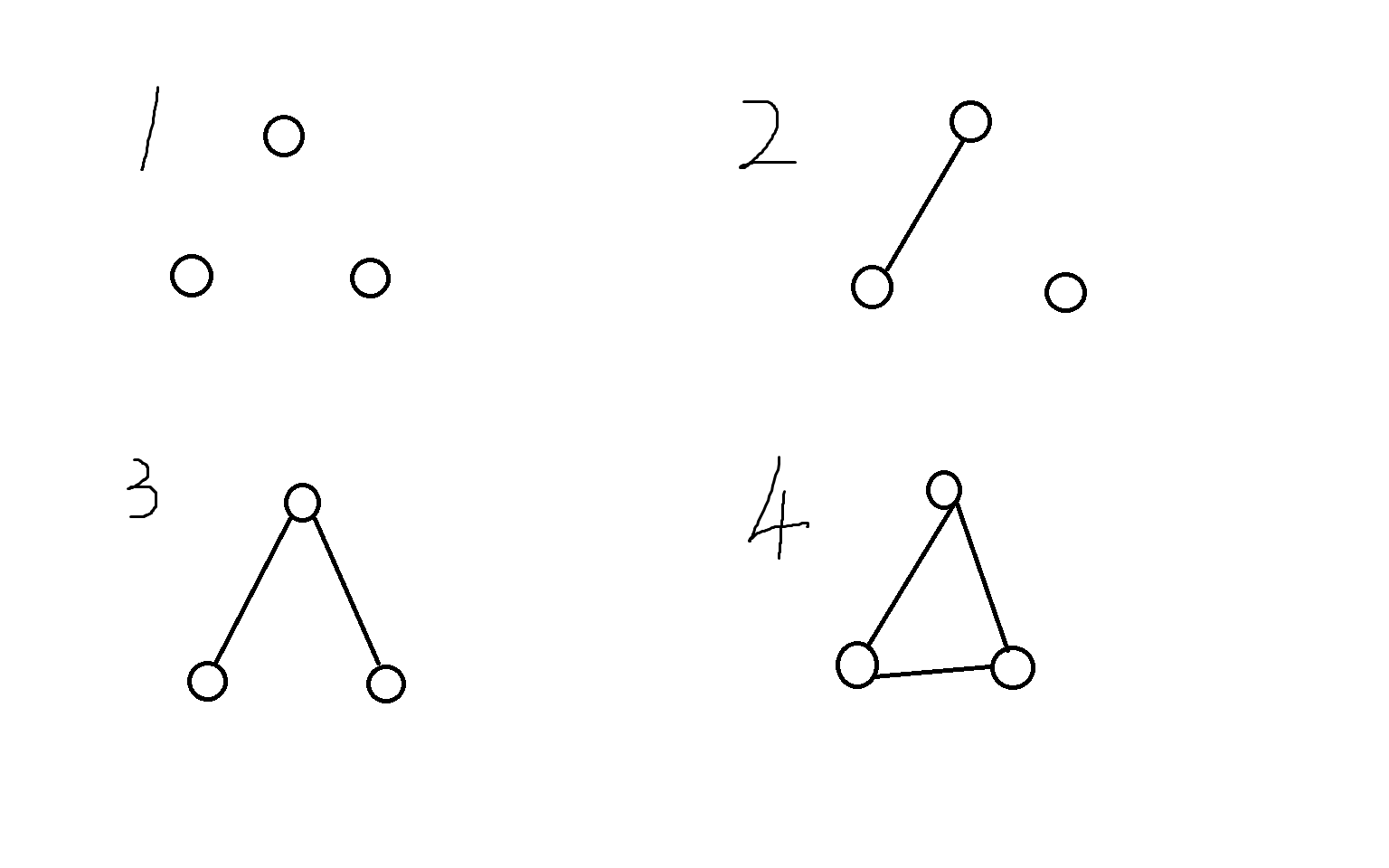
于是,我们只需要求出\(deg_i\)表示第\(i\)个矩阵有交的数量
代码就不贴了,扫描线和线段树我也不会。



