20240930模拟赛

T1连珠风暴
（necklace.pas/c/cpp）
问题描述：

• 给定M种颜色的珠子，每种颜色珠子的个数均不限，将这些珠子做成长度为N的项链。
  问能做成多少种不重复的项链.
  并且两条项链相同，当且仅当两条项链通过旋转或是翻转后能重合在一起，且对应珠子的颜色相同。

样例输入：

• 2 5

样例输出：

• 8

下图是样例解释：

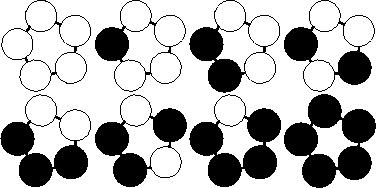
数据范围：

• 30%： n,m<=4
• 60%: n,m<=5
• 100%: nm<=32

由于范围非常小，所以我们只需要暴力枚举，复杂度是\(O(n^m n ^2)\)

code

#include <bits/stdc++.h>
using namespace std;
#define int long long

int m, n, ans, tot;
int f[40], d[40];

map <int, bool> mp;

bool check()
{
	tot = 0;
	for(int k = 0;k < n;k++)
	{
		int cnt = 0;
		for(int i = 0 + k;i < n + k;i++)
		{
			int j = i % n;
			cnt = cnt * m + f[j];
		}
		if(mp[cnt] == 1) return 0;
		d[++tot] = cnt;
	}
	reverse(f, f + n);
	for(int k = 0;k < n;k++)
	{
		int cnt = 0;
		for(int i = 0 + k;i < n + k;i++)
		{
			int j = i % n;
			cnt = cnt * m + f[j];
		}
		if(mp[cnt] == 1) return 0;
		d[++tot] = cnt;
	}
	for(int i = 1;i <= tot;i++) mp[d[i]] = 1;
	reverse(f, f + n);
	return 1;
}

void dg(int dep)
{
	if(dep == n)
	{
		if(check()) 
		{
			ans++;
		}
		return;
	}
	else
	{
		for(int i = 0;i < m;i++)
		{
			f[dep] = i; 
			dg(dep + 1);
		}
	}
}

signed main()
{
	freopen("necklace.in", "r", stdin);
	freopen("necklace.out", "w", stdout);
	cin >> m >> n;
	if(m == 1)
	{
		cout<<1<<"\n";
		return 0;
	}
	if(n == 1)
	{
		cout<<m<<"\n";
		return 0;
	}
	dg(0);
	cout<<ans<<"\n";
	return 0;
}

T2道路修建
问题描述：

• 为了保护放牧环境，避免牲畜过度啃咬同一个地方的草皮，牧场主决定利用不断迁移牲畜进行喂养的方法去保护牧草。然而牲畜在迁移过程中也会啃食路上的牧草，所以如果每次迁移都用同一条道路，那么该条道路同样会被啃咬过度而遭受破坏。
  现在牧场主拥有F个农场，已知这些农场至少有一条路径连接起来（不一定是直接相连），但从某些农场去另外一些农场，至少有一条路可通行。为了保护道路上的牧草，农场主希望再建造若干条道路，使得每次迁移牲畜时，至少有2种迁移途径，避免重复走上次迁移的道路。已知当前有的R条道路，问农场主至少要新建造几条道路，才能满足要求？
  输入描述
  第一行2个正整数，分别为n和m
  以下m行，每行2个数，表示连接的编号
  输出描述：
  一行一个数，表示至少新建的道路数目。
  样例输入：
  *7 7
  1 2
  2 3
  3 4
  2 5
  4 5
  5 6
  5 7
  样例输出：
  *2

数据范围：

• 30%：n<=10 m<=20
• 60%: n<=100 m<=2000
• 100%: n<=100000 m<=500000

此题是边双联通分量模版，但我不会。
边双联通分量的定义是在一张连通的无向图中，对于两个点\([u]\)和\([v]\)，如果无论删去哪条边（只能删去一条）都不能使它们不连通，我们就说 \([u]\)和\([v]\)边双连通。所以此题转化为至少需要添加几条边使之变为边双联通图。
由于我对图论中的联通性问题一窍不通，所以先引入割点的概念，再介绍tarjan算法。
割点

• 对于一个无向图，如果把一个点删除后这个图的极大连通分量数增加了，那么这个点就是这个图的割点（又称割顶）
• 朴素的想法，暴力删除每一个点，再用dfs判断是否联通，复杂度\(O(n(n + m))\),复杂度过高，考虑tarjan。

1. 我们按照dfs序给每个点打上时间戳。
   2.定义num[u],记录DFS对每个点的访问顺序， low[v],记录v和v的后代能连回的祖先num。如果low[v] >= num[u], 就说明在v这条支路上， 没有回退边连回u的祖先。

边双

• 在DFS的过程中，low值相同的点在一个边双联通分量，再把每一个边双联通分量缩成一个点，问题转化为至少在树上增加几条边能使这棵树变为一个边双联通分量。
• 易推导ans = (度为1的点数 + 1） \(/\) 2。
  code

#include <bits/stdc++.h>
using namespace std;
#define int long long

const int N = 100005;

int n, m, low[N], dfn;
vector <int> g[N];

void dfs(int u, int fa)
{
	low[u] = ++dfn;
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		if(v == fa) continue;
		if(!low[v]) dfs(v, u);
		low[u] = min(low[u], low[v]);
	}
}

int tarjan(){
	int degree[N];
	memset(degree, 0, sizeof degree);
	for(int i = 1;i <= n;i++)
		for(int j = 0;j < g[i].size(); j++)
			if(low[i] != low[g[i][j]])
				degree[low[i]]++;
	int res = 0;
	for(int i = 1;i <= n;i++)
		if(degree[i] == 1) res++;
	return res;
}

signed main()
{
	freopen("road.in", "r", stdin);
	freopen("road.out", "w", stdout);
	cin >> n >> m;
	for(int i = 1;i <= m;i++)
	{
		int a, b;
		cin >> a >> b;
		g[a].push_back(b);
		g[b].push_back(a);
	}
	dfn = 0;
	dfs(1, -1);
	int ans = tarjan();
	cout<<(ans + 1) / 2<<"\n";
	return 0;
}