深度学习中的优化方法（一）

写在前面：梯度下降法是深度学习优化的基础，因此本文首先探讨一维优化算法，然后扩展到多维。本文根据《最优化导论》(孙志强等译)的内容整理而来，由于笔者水平和精力有限，在此只是在简单层面做一个理解，如果要追求更严谨的数学理论，请大家参考相关书籍。在本文中，我们讨论目标函数为一元单值函数 \(f:R\rightarrow R\) 的最优化问题（即一维问题）的迭代求解方法。多维函数的梯度优化算法将在后续给出。

一维搜索方法从初始搜索点 \(x^{(0)}\) 出发，在迭代过程中，根据当前搜索点 \(x^{(k)}\) 和目标函数 \(f\) 构建一下一个搜索点 \(x^{(k+1)}\)，从而产生一个迭代序列 \(x^{(1)}, x^{(2)},...\)。本小节主要介绍以下算法：

1. 黄金分割法（只使用目标函数值 \(f\)）
2. 二分法（只使用目标函数的一阶导数 \(f'\)）
3. 牛顿法（使用目标函数的一阶和二阶导数 \(f',f''\)）

一、 黄金分割法

黄金分割法可以求解一元单值函数\(f:R \rightarrow R\) 在闭区间 \([a_{0},b_{0}]\) 上的极小值点，该方法的前提就是在区间 \([a_{0},b_{0}]\) 内存在唯一单峰，即存在唯一的极小值点 \(x^{*}\)。该方法的思路如下：

1. 在区间内寻找两个点 \(a_{0}, b_{0}\)，并使其满足：\(a_{0}-a_{1}=b_{0}-b_{1}=\lambda(b_{0}-a_{0}),\lambda<\dfrac{1}{2}\);
2. 计算目标函数在\(a_{1}, b_{1}\)处的值，如果 \(f(a_{1})<f(b_{1})\)，则 \(x^{*}\in[a_{0},b_{1}]\)；如果 \(f(a_{1})>f(b_{1})\)，则 \(x^{*}\in[a_{1},b_{0}]\)。如此往复，继续在区间内进行压缩，直到满足误差条件（可以设置为压缩后的区间长度，上一次和下一次之间的差值等）;
3. 以 \(f(a_{1})<f(b_{1})\) 为例，此时 \(x^{*}\in[a_{0},b_{1}]\)，由于 \(a_{1}\) 已经在区间内，因此可令 \(b_{2}=a_{1}, f(b_{2})=f(a_{1})\)，这样下一次迭代时便只需要重新计算 \(a_{2}\) 和 \(f(a_{2})\) 即可。整个过程如下图所示：

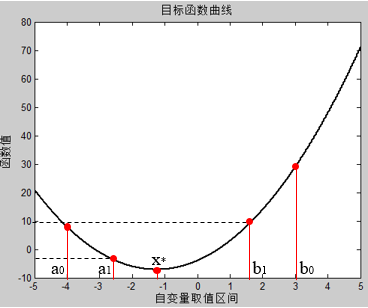
我们假设 \([a_{0}, b_{0}]\) 的区间长度为1， 进一步地，我们将上述的区间收缩关系表示成下图：

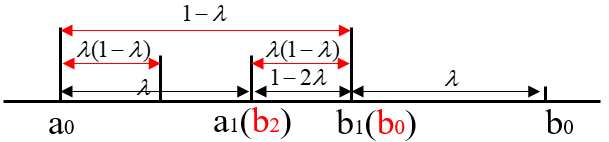
从图中我们可以得到如下的关系：\(\lambda(1-\lambda)=1-2\lambda\)，由于 \(\lambda<\dfrac{1}{2}\)，解得：\(\lambda = \dfrac{3-\sqrt{5}}{2} \approx 0.382\)。

又由于\(\dfrac{|b_{0}b_{1}|}{|a_{0}b_{1}|}=\dfrac{|a_{0}b_{1}|}{|a_{0}b_{0}|}\)，即 \(\dfrac{\lambda}{1-\lambda}=\dfrac{1-\lambda}{1}\)，因此这种划分空间的方式服从黄金分割法则，所以此方法被称为黄金分割法。

利用黄金分割法求解函数 \(f(x)=x^{4}-14x^{3}+60x^{2}-70x\) 的MATLAB代码如下：

function [xmin, ymin] = goldensearch( Start, End, e )
%   黄金分割法在闭区间进行一维搜索
%   输入参数：Start代表区间开始位置，End代表区间结束位置，e代表目标区间长度
%   输出参数：xmin表示取得最小值时的坐标，ymin表示求得的最小值
left = Start; right = End; %收敛区间
length = e;     %收敛精度
r = (sqrt(5)-1)/2;  %收敛比例
step = 0;   % 迭代次数初始化
f = f = @(x)2*x^2+5*x-4;;
while right-left>length
    step = step+1;
    a1 = left+(1-r)*(right-left);
    b1 = left+r*(right-left);
    ya1 = feval(f, a1);  %计算两端的函数值
    yb1 = feval(f, b1);
    if ya1 < yb1
        right = b1;
        b1 = a1;
        yb1 = ya1;
        a1 = left+r*(right-left);
        ya1 = feval(f, a1);
    else
        left = a1;
        b1 = a1;
        yb1 = ya1;
        a1 = left+(1-r)*(right-left);
        ya1 = feval(f, a1);
    end
end
%% 输出
xmin = (left+right)/2;
ymin = feval(f, xmin);
fprintf('程序经过%d次迭代的最小值点为%d,最小值为%d\n ',step,xmin,ymin)
%% 绘制图像
x = Start:0.01:End;
y = 2*x^2+5*x-4;
plot(x,y)
hold on
plot(xmin,ymin,'r*') % 在图像中标出极小值点
end

二、二分法

与黄金分割法相同，二分法同样是解决一元单值函数\(f:R \rightarrow R\) 在闭区间 \([a_{0},b_{0}]\) 上的极小值点，该方法的前提就是在区间 \([a_{0},b_{0}]\) 内存在唯一单峰，即存在唯一的极小值点 \(x^{*}\)。但是二分法使用目标函数的一阶导数来压缩区间，因此要求函数 \(f(x)\) 是连续可微的。二分法的思路比较简单，具体如下：

1. 确定区间的中点 \(x_{0}=(left+right)/2\)
2. 判断目标函数 \(f(x)\) 的导数 \(f'(x)\) 在 \(x_{0}\) 处的正负，如果 \(f'(x_{0})>0\)，那么极小值点 \(x^{*}\in [a_{0},x_{0}]\)；如果 \(f'(x_{0})<0\)，那么极小值点 \(x^{*}\in [x_{0},b_{0}]\)；
3. 收缩区间，继续进行迭代求解。

利用二分法求解函数 \(f(x)=cos(x)\) 在区间 \([0, 2\pi]\) 的最小值的MATLAB代码如下：

function [xmin, ymin] = binarysearch( Start, End, e )
%   二分法在闭区间进行一维搜索
%   输入参数：Start代表区间开始位置，End代表区间结束位置，e代表目标区间长度
%   输出参数：xmin表示取得最小值时的坐标，ymin表示求得的最小值
left = Start; right = End; %收敛区间
length = e;     %收敛精度
step = 0;   % 迭代次数初始化
f = @(x)cos(x);	% 目标函数
F = @(x)-sin(x); % 目标函数的一阶导数
while right-left>length
    step =step+1;
    x0=(left+right)/2;
    if feval(F, x0) > 0
        right=x0;
    else
        left=x0;
    end
end
%% 输出
xmin = (left+right)/2;
ymin = feval(f, xmin);
fprintf('程序经过%d次迭代的最小值点为%d,最小值为%d\n ',step,xmin,ymin)
%% 绘制图像
x = Start:0.01:End;
y = cos(x);
plot(x,y)
hold on
plot(xmin,ymin,'r*') % 在图像中标出极小值点
end

三、牛顿法

牛顿法假设目标函数一阶和二阶可微，即在 \(x^{(k)}\) 处的 \(f'(x^{(k)}),f''(x^{(k)})\) 均可求得，根据泰勒级数的展开式，任意的函数都可以近似于在任意一点 \(x^{k}\) 处：

\[q(x)=f(x^{k})+f'(x^{k})(x-x^{k})+\dfrac{1}{2}f''(x^{k})(x-x^{k})^{2} \]

因此，求解函数 \(f(x)\) 的极小值点可以近似为求解函数 \(q(x)\) 的极小值点，设 \(q(x)\) 的极小值点为 \(x^{k+1}\)，那么 \(x^{k+1}\) 满足：

\[\dfrac{dq(x)}{dx}|_{x=x^{k+1}}=f'(x^{k})+f''(x^{k})(x^{k+1}-x^{k})=0 \]

解得：\(x^{k+1}=x^{k}-\dfrac{f'(x^{k})}{f''(x^{k})}\)

牛顿法的更新公式类似于梯度下降法：\(x^{k+1} = x^{k}-\alpha f'(x^{k})\)，只不过在牛顿法中，学习率 \(\alpha\) 变成了二阶导数的倒数 \(\dfrac{1}{f''(x^{k})}\)。

对于区间内所有的自变量，当 \(f''(x)>0\) 时，牛顿法能够正常运行，但是当 \(f''(x)<0\) 时，牛顿法可能收敛到极大值点，如下图所示：

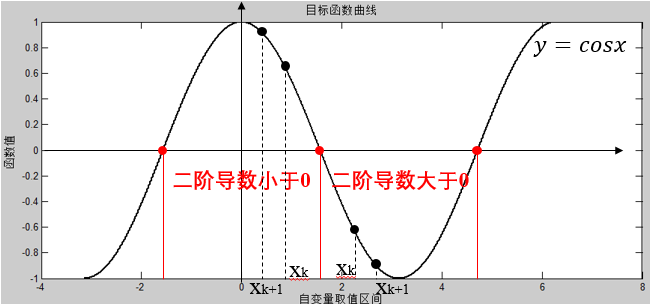
利用牛顿法求解函数 \(f(x)=\dfrac{x^{2}}{2}\) 的MATLAB代码如下：

function [xmin, ymin] = newton( start, e )
%   牛顿法求解局部最优解
%   输入参数：start代表自变量初始值，e表示x^{k+1}与x^{k}之间的差值
%   输出参数：xmin表示取得最小值时的坐标，ymin表示求得的最小值
length = e;     %收敛精度
step = 0;   % 迭代次数初始化
f = @(x)x^2/2;
F = @(x)x;
while step<=50
    step =step+1;
    x1 = start-feval(F, start);
    f_x0 = feval(f, start); f_x1 = feval(f, x1);
    if abs(f_x0-f_x1) <= length
        break;
    end
    start = x1;
    x1 = start-feval(F, start);
end
%% 输出
xmin = (start+x1)/2;
ymin = feval(f, xmin);
fprintf('程序经过%d次迭代的最小值点为%d,最小值为%d\n ',step,xmin,ymin)
%% 绘制图像
x = -20:0.0001:20;
y = x.^2/2;
plot(x,y)
hold on
plot(xmin,ymin,'r*') % 在图像中标出极小值点
end