| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 18计师班 |
| 这个作业要求链接 | 作业要求 |
| 我的课程学习目标 | 1、体验软件项目开发中的两人合作,练习结对编程; 2、掌握Github协作开发程序的操作方法。 |
| 这个作业在哪些方面帮助我实现学习目标 | 1、阅读《现代软件工程—构建之法》第3-4章内容,理解并掌握代码风格规范、代码设计规范、代码复审、结对编程概念; 2、软件开发能力、合作能力以及学习工具的使用能力等方面。 |
| 结对方学号-姓名 | 201871010134-周英杰 |
| 结对方本次博客作业链接 | 博客链接 |
| 本项目Github的仓库链接地址 | 仓库链接 |
任务1:阅读《现代软件工程—构建之法》第3-4章内容,理解并掌握代码风格规范、代码设计规范、代码复审、结对编程概念;
- 代码风格规范:就是代码格式的一些要求。主要有以下几个方面:
- 缩进
- 行宽
- 括号
- 断行与空白的{}行
- 分行
- 命名
- 下划线
- 大小写
- 注释
代码风格规范的原则是简明、易读、无二异性。
- 代码设计规范:不光是程序书写的格式问题,而且牵涉到程序设计、模块之间的关系、设计模式等方方面面。主要体现在以下几个方面:
- 函数
- goto
- 错误处理
- 参数处理
- 断言
- 如何处理C++中的类
- 类
- class vs.struct
- 公共/保护/私有成员(public、protected和private)
- 数据成员
- 虚函数
- 构造函数
- 折构函数
- new和delete
- 运算符(Operators)
- 异常(Exceptions)
- 类型继承(Class Inheritance)
- 代码复审:查看代码是否符合代码规范,找出软件开发过程中的错误,降低软件开发后期维护的难度,提高软件的质量和可靠性。
- 结对编程:结对编程中有两个角色:领航员和驾驶员。在个人编写的过程中,很多人喜欢根据个人喜好来规定代码规范,而且存在的bug自己难以发现,因此,在结对编程时,我们可以互换角色,在开始写代码之前,规定两个人都认可的一套代码规范,并且不间断地进行复审,以减少软件中存在的问题,修复bug,提高软件质量。
任务2:两两自由结对,对结对方《实验二 软件工程个人项目》的项目成果进行评价,具体要求如下:
(1)对项目博文作业进行阅读并进行评论,评论要点包括:博文结构、博文内容、博文结构与PSP中“任务内容”列的关系、PSP中“计划共完成需要的时间”与“实际完成需要的时间”两列数据的差异化分析与原因探究,将以上评论内容发布到博客评论区。
(2)克隆结对方项目源码到本地机器,阅读并测试运行代码,参照《现代软件工程—构建之法》4.4.3节核查表复审同伴项目代码并记录。
(3)依据复审结果尝试利用github的Fork、Clone、Push、Pull request、Merge pull request等操作对同伴个人项目仓库的源码进行合作修改。
| 提出问题 | 执行情况 |
|---|---|
| 概要部分 | |
| 代码符合需求和规格说明么? | 代码符合需求和对反说明。 |
| 代码设计是否考虑周全? | 考虑周全。 |
| 代码可读性如何? | 可以顺利读下去。 |
| 代码容易维护么? | 不太容易维护。 |
| 代码的每一行都执行并检查过了吗? | 是的,都可以执行。 |
| 设计规范部分 | |
| 设计是否遵从已知的设计模式或项目中常用的模式? | 遵从。 |
| 代码有没有依赖于某一平台,是否会影响将来的移植(如Win32到Win64)? | 没有,不会影响移植,任何平台都可以。 |
| 开发者新写的代码能否用已有的Library/SDK/Framework中的功能实现?在本项目中是否存在类似的功能可以调用而不用全部重新实现? | 可以用;存在,有些代码是可以调用的 |
| 有没有无用的代码可以清除?(很多人想保留尽可能多的代码,因为以后可能会用上,这样导致程序文件中有很多注释掉的代码,这些代码都可以删除,因为源代码控制已经保存了原来的老代码) | 基本清楚完毕了。 |
| 代码规范部分 | |
| 修改的部分符合代码标准和风格么? | 修改的部分不太符合代码标准和风格。 |
| 具体代码部分 | |
| 有没有对错误进行处理?对于调用的外部函数,是否检查了返回值或处理了异常? | 对错误都进行了处理,没有异常。 |
| 参数传递有无错误,字符串的长度是字节的长度还是字符(可能是单/双字节)的长度,是以0开始计数还是以1开始计数? | 无错误;本项目中是以0开始计数。 |
| 边界条件是如何处理的?switch语句的default分支是如何处理的?循环有没有可能出现死循环? | switch语句的default分支返回false,没有出现死循环。 |
| 有没有使用断言(Assert)来保证我们认为不变的条件真的得到满足? | 有。 |
| 对资源的利用是在哪里申请,在哪里释放的?有没有可能导致资源泄露(内存、文件、各种GUI资源、数据库访问的连接,等等)?有没有优化的空间? | 在对数据库进行操作之前申请数据库连接资源,操作完毕之后释放申请的资源;不会导致资源泄露;可以优化使用断言来保证我们认为不变的条件 |
| 数据结构中有没有用不到的元素? | 没有。 |
| 效能 | |
| 代码的效能(Performance)如何?最坏的情况如何? | 达到了具体任务的要求。 |
| 代码中,特别是循环中是否有明显可优化的部分(C++中反复创建类,C#中 string 的操作是否能用StringBuilder 来优化)? | 没有,已经比较优化了。 |
| 对于系统和网络调用是否会超时?如何处理? | 目前没有出现超时的现象。假如出现了我们会杀毒;整理系统,减少运行的进程,释放内存、cpu,释放c盘空间。 |
| 可读性 | |
| 代码可读性如何?有没有足够的注释? | 可以顺利读取;代码有足够的注释让我们读懂 |
| 可测试性 | |
| 代码是否需要更新或创建新的单元测试?针对特定领域的开发(如数据库、网页、多线程等),可以整理专门的核查表。 | 可以继续开发,摆脱传统的命令行方式,更为实用。 |
任务3:采用两人结对编程方式,设计开发一款D{0-1}KP 实例数据集算法实验平台,使之具有以下功能:
(1)平台基础功能:实验二 任务3;
(2)D{0-1}KP 实例数据集需存储在数据库;
(3)平台可动态嵌入任何一个有效的D{0-1}KP 实例求解算法,并保存算法实验日志数据;
(4)人机交互界面要求为GUI界面(WEB页面、APP页面都可);
(5)查阅资料,设计遗传算法求解D{0-1}KP,并利用此算法测试要求(3);
(6)附加功能:除(1)-(5)外的任意有效平台功能实现。
- 需求分析陈述
- 设计实现人机交互界面
- 查阅相关资料,运用遗传算法求解 D{0-1}KP
- 将D{0-1}KP 实例数据集存储在数据库
- 平台可动态嵌入任何一个有效的D{0-1}KP 实例求解算法,并保存算法实验日志数据
- 软件设计说明
- D{0-1}KP数据可以保存到数据库,也可以从数据库中清除;
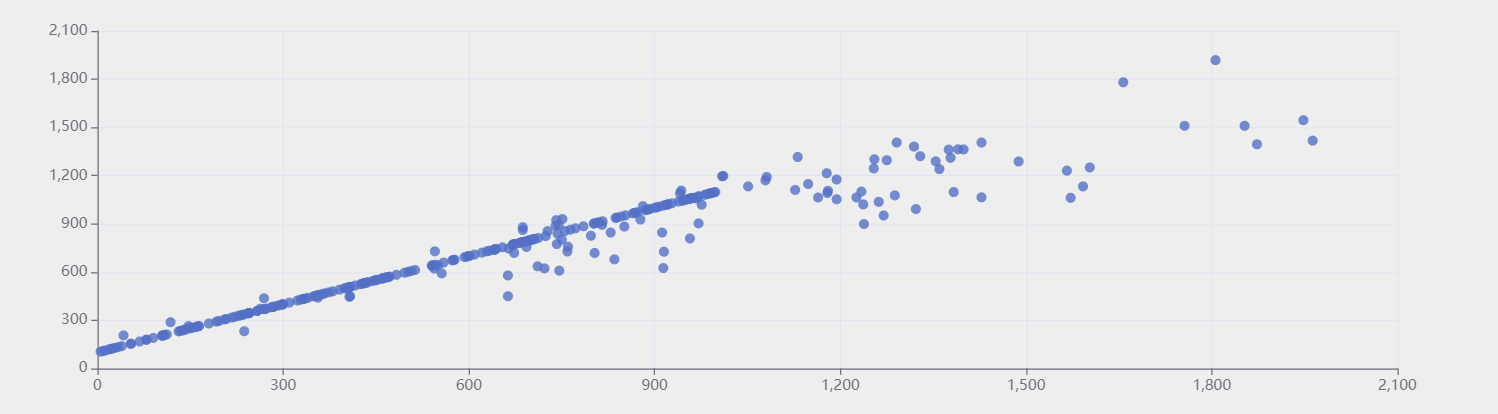
- 绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图;
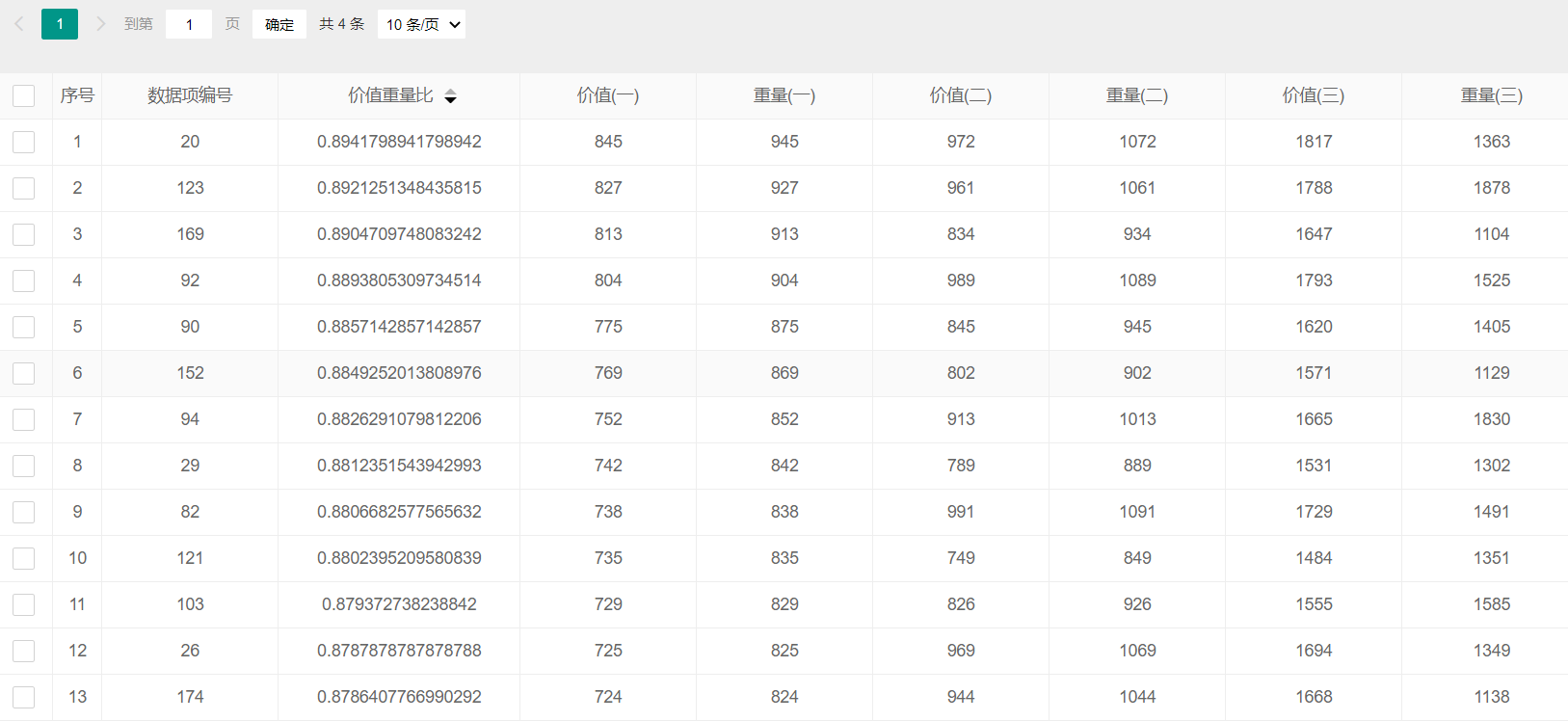
- 对任意一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序;
- 用户能够自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间(以秒为单位);
- 对任意一组D{0-1} KP数据的最优解、求解时间和解向量;
- 后台编写遗传算法求解D{0-1}KP。
- 软件实现及核心功能代码展示
- 遗传算法介绍
- 1、编码:问题可以表示为一个n位的二进制码,第i位表示物品i,数值为0表示物品没有选中,1表示选中物品。
- 2、种群:种群是个体的集合。
- 3、适应度:适应度在0-1背包问题中表示的是背包中的总价值的大小,总价值越大个体的适应度越大。
- 4、选择:从种群中选出部分个体之后进行重组或交叉,产生的新个体依据适应度函数进行优胜劣汰,选出优良个体。
- 5、交叉:同的个体之间随机的进行杂交,其基因进行再次重组。其后产生新的具有不同适应度的新个体。
- 6、变异:变异指单个个体的基因按照小概率进行变化的方法。本题中采用的变异方法随机产生变异点,并进行了以下两种变异类型。
(1)变异点进行0和1的状态翻转。此方法趋于常规,但无甚缺点。
(2) 变异点变为1,如果超出背包容积,则变为0。此方法更易产生较大的解,但如若初始种群产生的不好,则随后的变异绝不会产生最优解。
- 遗传算法介绍
- 核心代码
(1)回溯算法
class Solution:
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
def backtrack(first = 0):
# if all integers are used up
if first == n:
output.append(nums[:])
for i in range(first, n):
# place i-th integer first
# in the current permutation
nums[first], nums[i] = nums[i], nums[first]
# use next integers to complete the permutations
backtrack(first + 1)
# backtrack
nums[first], nums[i] = nums[i], nums[first]
n = len(nums)
output = []
backtrack()
return output
(2)动态规划算法
def pack(w, v, n, c):
dp = [0 for _ in range(c+1)]
for i in range(1, len(w)+1):
for j in reversed(range(1, c+1)):
for k in range(3):
if j-w[i-1][k] >= 0:
# print(dp[j])
dp[j] = max(dp[j], dp[j-w[i-1][k]] + v[i-1][k])
# print(dp)
print(dp[c])
(3)遗传算法
def F(x, y):
return 3*(1-x)**2*np.exp(-(x**2)-(y+1)**2)- 10*(x/5 - x**3 - y**5)*np.exp(-x**2-y**2)- 1/3**np.exp(-(x+1)**2 - y**2)
def plot_3d(ax):
X = np.linspace(*X_BOUND, 100)
Y = np.linspace(*Y_BOUND, 100)
X,Y = np.meshgrid(X, Y)
Z = F(X, Y)
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap=cm.coolwarm)
ax.set_zlim(-10,10)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.pause(3)
plt.show()
def get_fitness(pop):
x,y = translateDNA(pop)
pred = F(x, y)
return (pred - np.min(pred)) #减去最小的适应度是为了防止适应度出现负数,通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)]
def translateDNA(pop): #pop表示种群矩阵,一行表示一个二进制编码表示的DNA,矩阵的行数为种群数目
x_pop = pop[:,1::2]#奇数列表示X,从索引列1开始,加入了步长2
y_pop = pop[:,::2] #偶数列表示y,从索引列1开始,加入了步长2
#pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
x = x_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(X_BOUND[1]-X_BOUND[0])+X_BOUND[0]
y = y_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(Y_BOUND[1]-Y_BOUND[0])+Y_BOUND[0]
return x,y
def crossover_and_mutation(pop, CROSSOVER_RATE = 0.8):
new_pop = []
for father in pop: #遍历种群中的每一个个体,将该个体作为父亲
child = father #孩子先得到父亲的全部基因(这里我把一串二进制串的那些0,1称为基因)
if np.random.rand() < CROSSOVER_RATE: #产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = pop[np.random.randint(POP_SIZE)] #再种群中选择另一个个体,并将该个体作为母亲
cross_points = np.random.randint(low=0, high=DNA_SIZE*2) #随机产生交叉的点
child[cross_points:] = mother[cross_points:] #孩子得到位于交叉点后的母亲的基因
mutation(child) #每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
def mutation(child, MUTATION_RATE=0.003):
if np.random.rand() < MUTATION_RATE: #以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE*2) #随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point]^1 #将变异点的二进制为反转
def select(pop, fitness): # nature selection wrt pop's fitness
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
p=(fitness)/(fitness.sum()) )
return pop[idx]
def print_info(pop):
fitness = get_fitness(pop)
max_fitness_index = np.argmax(fitness)
print("max_fitness:", fitness[max_fitness_index])
x,y = translateDNA(pop)
print("最优的基因型:", pop[max_fitness_index])
print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))
if __name__ == "__main__":
fig = plt.figure()
ax = Axes3D(fig)
plt.ion()#将画图模式改为交互模式,程序遇到plt.show不会暂停,而是继续执行
plot_3d(ax)
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE*2)) #matrix (POP_SIZE, DNA_SIZE)
for _ in range(N_GENERATIONS):#迭代N代
x,y = translateDNA(pop)
if 'sca' in locals():
sca.remove()
sca = ax.scatter(x, y, F(x,y), c='black', marker='o')
plt.show()
plt.pause(0.1)
pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
#F_values = F(translateDNA(pop)[0], translateDNA(pop)[1])#x, y --> Z matrix
fitness = get_fitness(pop)
pop = select(pop, fitness) #选择生成新的种群
print_info(pop)
plt.ioff()
plot_3d(ax)
- 程序运行
- 散点图
![]()
- 数据排序
![]()
- 动态规划算法
![]()
- 回溯算法
![]()
- 遗传算法
![]()
- 散点图
- 描述结对的过程,提供两人在讨论、细化和编程时的结对照片(非摆拍)。
![]()
- PSP流程
| PSP 各个阶段 | 自己预估的时间(分钟) | 实际的记录(分钟) |
|---|---|---|
| 计划: 明确需求和其他因素,估计以下的各个任务需要多少时间 | 2*60 | 3*60 |
| 开发 (包括下面 8 项子任务) | 37*60 | 41*60 |
| · 需求分析 (包括学习新技术、新工具的时间) | 3*60 | 3*60 |
| · 生成设计文档 (整体框架的设计,各模块的接口,用时序图,快速原型等方法) | 2*60 | 2*60 |
| · 设计复审 (和同事审核设计文档,或者自己复审) | 1*60 | 1*60 |
| · 代码规范 (为目前的开发制定或选择合适的规范) | 1*60 | 1*60 |
| · 具体设计(用伪代码,流程图等方法来设计具体模块) | 3*60 | 4*60 |
| · 具体编码 | 25*60 | 25*60 |
| · 代码复审 | 1*60 | 2*60 |
| · 测试(自我测试,修改代码,提交修改) | 1*60 | 3*60 |
| 报告 | 1*60 | 2*60 |
| 测试报告 | 1*60 | 2*60 |
| 计算工作量 (多少行代码,多少次签入,多少测试用例,其他工作量) | 1*60 | 2*60 |
| 事后总结, 并提出改进计划 (包括写文档、博客的时间) | 2*60 | 3*60 |
| 总共花费的时间 (分钟) | 44*60 | 53*60 |
- 小结感受
- 与结对对象相互交流与合作,是可以带来1+1>2的效果。
- 在编程中遇到问题要及时交流,相互讨论。
- 在项目过程中要相互监督,提高效率。
- 在编程过程中要时刻注意代码规范问题,会为后续修改带来很多的便利。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号