Leetcode 1203. Sort Items by Groups Respecting Dependencies
Description
There are n items each belonging to zero or one of m groups where group[i] is the group that the i-th item belongs to and it's equal to -1 if the i-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.
Return a sorted list of the items such that:
- The items that belong to the same group are next to each other in the sorted list.
- There are some relations between these items where beforeItems[i] is a list containing all the items that should come before the i-th item in the sorted array (to the left of the i-th item).
Return any solution if there is more than one solution and return an empty list if there is no solution.
Example 1:
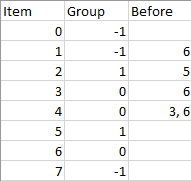
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
Output: [6,3,4,1,5,2,0,7]
Example 2:
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
Output: []
Explanation: This is the same as example 1 except that 4 needs to be before 6 in the sorted list.
Constraints:
- \(1 <= m <= n <= 3*10^4\)
- group.length == beforeItems.length == n
- -1 <= group[i] <= m-1
- 0 <= beforeItems[i].length <= n-1
- 0 <= beforeItems[i][j] <= n-1
- i != beforeItems[i][j]
- beforeItems[i] does not contain duplicate elements
这题的主要考察点是拓扑排序,之前自己的想法是对每个group进行拓扑排序,然后将牌号的group当作一个新的item,但是这种想法实现比较麻烦。这题给人的主要启发就是看问题不要陷入到局部,要从宏观的角度看。参考大佬的思路后总结如下:
这个问题可以看作是两层拓扑排序的问题。
- 对group进行拓扑排序;
- 对每个group内的item进行拓扑排序;
Python实现
from collections import defaultdict
class Solution:
def sortItems(self, n: int, m: int, group: List[int], beforeItems: List[List[int]]) -> List[int]:
def topo_sort(points, front, back):
order = []
que = []
for p in points:
if not front[p]:
que.append(p)
while que:
p = que.pop(0)
order.append(p)
for i in back[p]:
front[i].discard(p)
if not front[i]:
que.append(i)
return order if len(order) == len(points) else []
grp_itms = defaultdict(set)
for i in range(n):
if group[i] == -1:
group[i] = m
m += 1
grp_itms[group[i]].add(i)
itm_front, itm_back = defaultdict(set), defaultdict(set)
grp_front, grp_back = defaultdict(set), defaultdict(set)
for i in range(n):
for j in beforeItems[i]:
if group[i] == group[j]:
itm_front[i].add(j)
itm_back[j].add(i)
else:
grp_front[group[i]].add(group[j])
grp_back[group[j]].add(group[i])
# 对group拓扑排序
grp_sort = topo_sort(grp_itms.keys(), grp_front, grp_back)
if len(grp_sort) != len(grp_itms.keys()):
return []
res = []
for g in grp_sort:
items = grp_itms[g]
#对group内的items进行拓扑排序
itm_sort = topo_sort(items, itm_front, itm_back)
if len(itm_sort) != len(items):
return []
res += itm_sort
return res


