2015年新西兰数学奥林匹克第三题解答

新西兰数学奥林匹克总计3道题目, 考试时间为90分钟.

 

在 $\triangle{ABC}$ 三边外侧作 $\triangle{BPC}, \triangle{QAC}, \triangle{ARB}$. $\angle{PBC} = \angle{CAQ} = 45^\circ$, $\angle{BCP} = \angle{QCA} = 30^\circ$, $\angle{ABR} = \angle{BAR} = 15^\circ$. 证明: $QR\perp RP$, $QR = RP$.

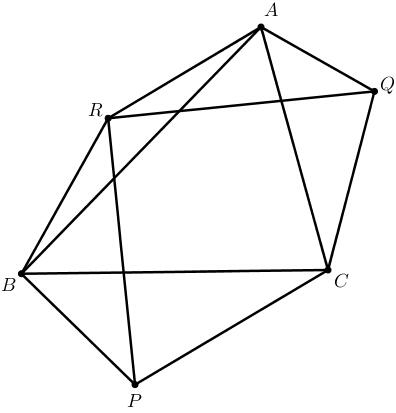
解答:

易知 $\angle{ARB} = 180^\circ - 30^\circ = 150^\circ$, 因此需要证明 $\angle{ARQ} + \angle{BRP} = 60^\circ$.

由已知 $\angle{PBC} = \angle{CAQ} = 45^\circ$ 及 $\angle{ABR} = \angle{BAR} = 15^\circ$, 考虑将 $\triangle{ARQ}$ 及 $\triangle{BRP}$ 分别绕 $A, B$ 两点旋转在 $AB$ 外侧形成正三角形, 即以 $AB$ 为边作正三角形 $ABX$, 连结 $XR$, $XC$ (如下图所示).

 

 

此时需证明 $\angle{ARQ} = \angle{AXC}$ 及 $\angle{BRP} = \angle{BXC}$, 即需证明 $\triangle{ARQ}\sim\triangle{AXC}$ 及 $\triangle{BRP}\sim\triangle{BXC}$. 由于已知一角相等, 待证另一角相等, 因此考虑证明如下等式 $${AR\over AX} = {AQ\over AC},\ {BR\over BX} = {BP\over BC}.$$ 这可由 $\triangle{AXR} \sim \triangle{ACQ}$ ($AA$) 及 $\triangle{BXR}\sim\triangle{BCP}$ ($AA$) 分别证明之.

由 $\triangle{ARQ}\sim\triangle{AXC}$ 及 $\triangle{BRP}\sim\triangle{BXC}$ 可知, $${QR\over XC} = {AR\over AX} = {BR \over BX} = {RP \over XC}\Rightarrow QR = RP.$$ Q.E.D.