腾讯课堂目标2017初中数学联赛集训队作业题解答-1

 

课程链接：目标2017初中数学联赛集训队-1（赵胤授课）

 

 

1、直角 $\triangle{ABC}$ 中, $AD$ 是斜边上的高, $I_1, I_2$ 是 $\triangle{ABD}, \triangle{ACD}$ 的内心, 求证: $B, C, I_2, I_1$ 四点共圆.

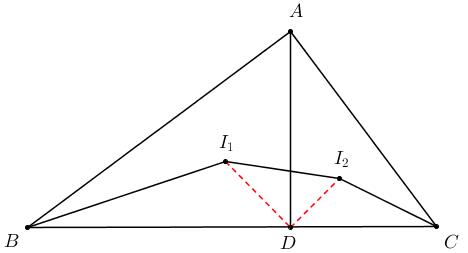
证明:

考虑证明 $$\angle{BI_1I_2} + \angle{BCI_2} = \angle{BI_1D} + \angle{DI_1I_2} + \angle{BCI_2} = 180^\circ.$$ 易知 $$\angle{BI_1D} = 180^\circ - {1\over2}(\angle{ABD} + \angle{ADB}) = 180^\circ - {1\over2}(180^\circ - \angle{BAD}) =90^\circ + {1\over2}\angle{BAD}.$$ 另一方面, $$\angle{BAC} = \angle{I_1DI_2} = 90^\circ,\ AB : AC = I_1D : I_2D\ (\because\triangle{ABD} \sim \triangle{CAD}).$$ 因此 $$\triangle{ABC} \sim \triangle{DI_1I_2}\Rightarrow \angle{ABC} = \angle{DI_1I_2},\ \angle{ACB} = \angle{DI_2I_1}.$$ 由此可得 $$\angle{BI_1I_2} + \angle{BCI_2} = \angle{BI_1D} + \angle{DI_1I_2} + \angle{BCI_2}$$ $$= 90^\circ + {1\over2}\angle{BAD}+ \angle{ABC} + {1\over2}\angle{ACB}$$ $$= 90^\circ + {1\over2}\angle{BAD}+ \angle{ABC} + {1\over2}\angle{BAD}$$ $$= 90^\circ + \angle{BAD}+ \angle{ABC} = 180^\circ.$$

Q.E.D.

 

 

2、在凸五边形 $ABCDE$ 中, 若 $\angle{ABC} = \angle{ADE}$, $\angle{AEC} = \angle{ADB}$, 求证: $\angle{BAC} = \angle{DAE}$.

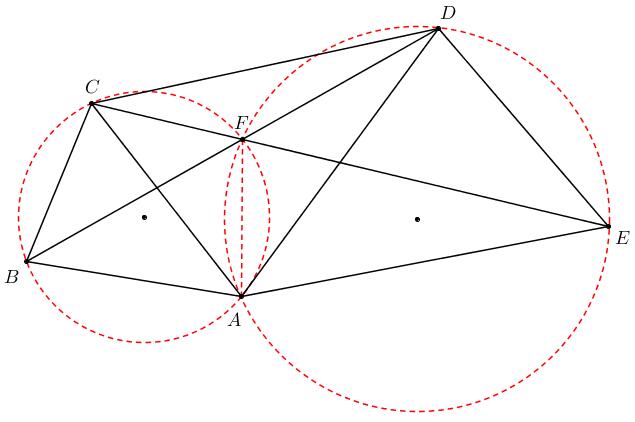
证明:

设 $BD, CE$ 交点为 $F$. 由 $\angle{AEC} = \angle{ADB}$ 知 $A, E, D, F$ 四点共圆.

再由 $\angle{ABC} = \angle{ADE} = \angle{AFE}$ 知 $A, B, C, F$ 四点共圆.

由此可得 $\angle{BAC} = \angle{BFC} = \angle{DFE} = \angle{DAE}$.

Q.E.D.

 

 

3、在圆内引弦 $AB, AC$, $\angle{BAC}$ 的平分线交圆于点 $D$. 过 $D$ 作 $DE\perp AB$ 于 $E$, 求证: $AE = \displaystyle{1\over 2}(AB + AC)$.

证明:

考虑证明 $2AE = AB + AC$.

由角平分线性质及 $CD = BD$, 构造全等三角形, 作 $DF\perp AC$ (或其延长线)于 $F$.

易证 $\triangle{DFC}\cong\triangle{DEB}$ 及 $\triangle{DFA}\cong\triangle{DEA}$, 因此 $2AE = AE + AF = AB + AC$.

需要注意的是, 本题应说明当 $B, E$ 重合时之情形. 易知此时 $AD$ 为该圆直径, 结论依然成立.

Q.E.D.

 

 

4、在三角形 $ABC$ 中, $\angle{ACB} = 45^\circ$, $D$ 为 $AC$ 上一点且 $\angle{ADB} = 60^\circ$, $AB$ 切 $\triangle{BCD}$ 外接圆于 $B$, 求证: $AD:DC = 2:1$.

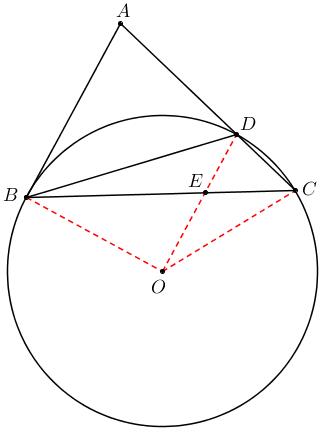
证明:

由于 $AD, DC$ 在同一条直线上, 考虑平行截割定理暨造出平行关系解决之.

连接 $OB$ 造出直角, 再由 $\angle{ACB} = 45^\circ$ 考虑再造出一个 $90^\circ$: $$\angle{BOD} = 2\angle{BCD} = 90^\circ.$$ 由此发现 $AB\parallel OD\Rightarrow AD:DC = BE:EC$. 接下来可以考虑证明 $BE:EC = 2:1$.

通过 $\triangle{ABC}\sim\triangle{ADB}$ 及简单的角度计算可知: $$\angle{ABC} = \angle{ADB} = 60^\circ\Rightarrow \angle{OBC} = 30^\circ\Rightarrow BE = 2OE,$$ $$\angle{DBC = 15^\circ}\Rightarrow \angle{DOC} = 30^\circ\Rightarrow EC = OE.$$ 由此可知 $BE = 2CE\Rightarrow AD = 2DC$.

Q.E.D.

 

 

5、设 $ABCD$ 是圆内接四边形, 对角线 $AC$ 与 $BD$ 交于 $X$, 从 $X$ 作 $AB, BC, CD, DA$ 的垂线, 垂足分别为 $A^\prime, B^\prime, C^\prime, D^\prime$, 求证: $A^\prime B^\prime + C^\prime D^\prime = A^\prime D^\prime + B^\prime C^\prime$.

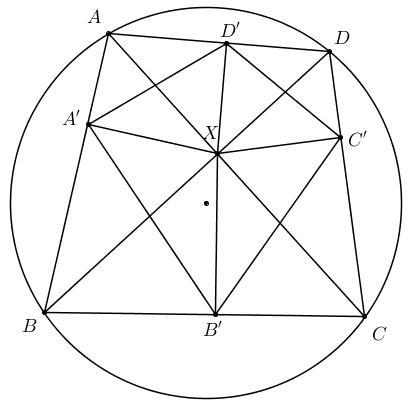
证明:

由已知的垂直关系可得 $A^\prime, B, B^\prime, X$ 四点共圆, 且其直径为 $BX$. 则由正弦定理有 $${BX\over\sin90^\circ} = {A^\prime B^\prime \over \sin\angle{A^\prime BB^\prime}}\Rightarrow {A^\prime B^\prime\over BX} = \sin\angle{A^\prime BB^\prime}.$$ 另一方面, 在 $ABCD$ 外接圆中同样有 $${AC\over d} = \sin\angle{A^\prime BB^\prime},$$其中 $d$ 为 $ABCD$ 外接圆之直径. 由此可知 $$A^\prime B^\prime = {BX\cdot AC\over d}.$$ 同理可得 $$C^\prime D^\prime = {DX\cdot AC\over d}.$$ 因此, $$A^\prime B^\prime + C^\prime D^\prime = BD\cdot{ AC \over d}.$$ 同理可得 $$B^\prime C^\prime + A^\prime D^\prime = AC\cdot{ BD \over d}.$$ 即 $A^\prime B^\prime + C^\prime D^\prime = A^\prime D^\prime + B^\prime C^\prime$.

Q.E.D.

 

 

6、四边形 $ABCD$ 内接于圆, 另一圆的圆心 $O$ 在边 $AB$ 上, 且与其余三边相切, 求证: $AD + BC = AB$.

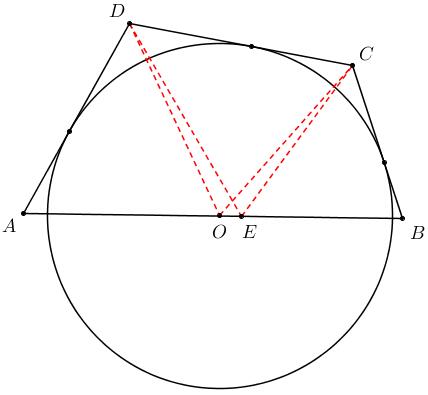
证明:

由证明结论考虑将 $AD, BC$ 平移到 $AB$上, 暨在 $AB$ 上截取 $BE = BC$, 证明目标为 $AE = AD$.

由 $A, B, C, D$ 四点共圆及切线性质可知 $$\angle{BEC} = \angle{BCE} = {1\over2}(180^\circ - \angle{EBC}) = {1\over2}\angle{ADC} = \angle{ODC},$$ 因此 $O, E, C, D$ 四点共圆. 由此可得 $$\angle{AED} = \angle{OCD} = {1\over 2}\angle{BCD} = {1\over2}(180^\circ - \angle{A}),$$即证明$AE = AD$.

Q.E.D.

 

 

7、两圆彼此外切于 $D$, 一直线切一圆于 $A$, 交另一圆于 $B, C$ 两点, 求证: $A$ 到直线 $BD, CD$ 之距离相等.

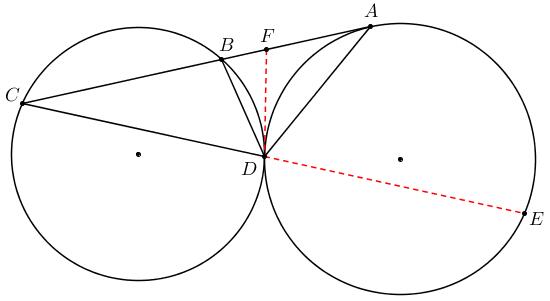
证明:

点到两直线(线段)距离相等, 可联想到角平分线之性质. 延长 $CD$ 交圆于 $E$, 考虑证明 $AD$ 是 $\angle{BDE}$ 之角平分线.

过点 $D$ 作两圆之公切线交 $AC$ 于 $F$, 可知 $$\angle{ADB} = \angle{ADF} + \angle{BDF} = \angle{DAF} +\angle{DCF} = \angle{ADE}.$$ 即证明 $AD$ 是 $\angle{BDE}$ 之角平分线.

Q.E.D.

 

 

 

扫描关注“奥数学苑”微信公众号(ID: aoshu_xueyuan)