七下三角形精讲——三角形基础以及全等判定

导言

应某人在几个世纪前的要求，经过了一个寒假的研究（其实是到现在才想起来）这篇文章就讲一下三角形

定义

三角形很好理解，三个角组成的图形
其实是三条直线首尾顺次相连组成的封闭图形

分类

按角分

按角分的三角形可以分成锐角三角形、直角三角形、钝角三角形
还有某些抽象的三角形现在接触不到，不用管它

按边分

等腰三角形 一般三角形
而等边三角形（又称正三角形）是属于等腰三角形的，他是特殊的等腰三角形

小学都学过，不展开讲

三角形面积

求法1：

小学知识

\[S=\frac{1}{2} ah \]

不说

求法2

三角形面积等于任意两边及其角的正弦值之积的一半
即：

\[S=\frac{1}{2} ab sin C \]

余弦定理，后面一篇文章专门讲
初中巨好用

求法3

令\(p=\frac{1}{2}(a+b+c)\)
则：$$S_{△ABC}=\sqrt{p(p-a)(p-b)(p-c)}$$
这就是海伦公式，也被称作秦九韶公式
某些特定题型超级好用

高级求法：

如果三角形在平面直角坐标系上的一个顶点为原点，另两个分别为\((x_1,y_1),(x_2,y_2)\)

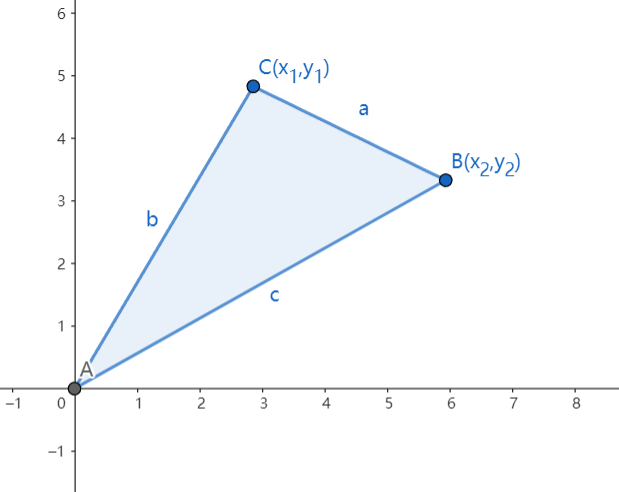
则

\[S_{△ABC}=\frac{1}{2} |x_1y_2-x_2y_1| \]

这是大学知识，选择填空放心用，大题用了可能扣分

三角形内角和

180°无需多言，用平行线易证，留做习题

三角形外角

三角形外角为不相邻两个内角之和，根据外角的定义用内角和倒出来

外角和

任何多边形外角和均为360°，三角形也不例外

三角形的一些小知识

1. 两边之和大于第三边
2. 两边之差小于第三边
3. 三角形的外角大于任何与之不相邻的内角
4. 在三角形中至少一个角大于60°，也至少有一个角小于等于60°
5. 三角形一边扩大，对应的角也会扩大

三角形的重要线段

中线(3条)

定义：连接三角形一个顶点以及其对边中点的线段

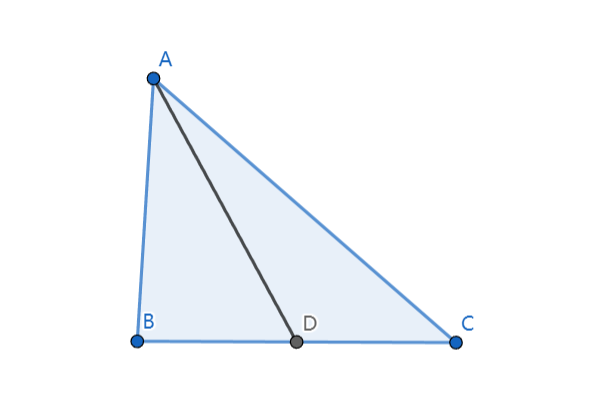
如图\(AD为△ABC中线\)
可以根据中线定义推出：

\[\begin{cases} BD=CD\\ S_{△ABD}=S_{△ACD} \end{cases} \]

高(3条)

定义：从一个顶点到对对边所在直线做垂线，顶点与垂足之间的线段被称作高
小学讲过，不说

角平分线(3条)

定义：三角形一个内角的平分线和这个角的对边相交，这个角的顶点与交点间的线段叫做三角形的角平分线

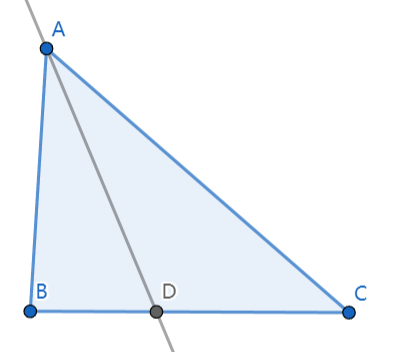
如图，\(AD为△ABC的角平分线\)

三角形的重心

定义：三角形所有中线的交点

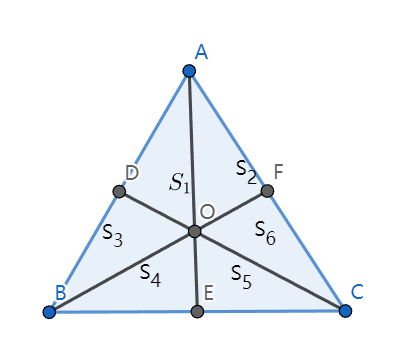
根据中线的定义易证\(S_1=S_2=S_3=S_4=S_5=S_6\)

三角形的全等

定义

全等的定义：完全重合的两个三角形互为全等三角形
符号：\(≌\)

性质

若有\(△ABC ≌ △DEF\)
则：

\[\begin{cases} S_{△ABC}=S_{△DEF} \\ AB=DE \\ AC=DF \\ BC=EF \\ h_{△ABC}=h_{△DEF} \\ \end{cases} \]

然后肯定边相等、角相等、啥都相等了

判定

边边边(SSS)

如图，\(AB=DE,AC=DF,BC=EF\)
则

\[∵在△ABC与△DEF中 \\ \begin{cases} AB=DE\\ BC=EF\\ AC=DF\\ \end{cases} \\ ∴ △ABC ≌ △DEF (SSS) \]

注意，写的时候需要一一对应

两边及其夹角相等 (SAS)

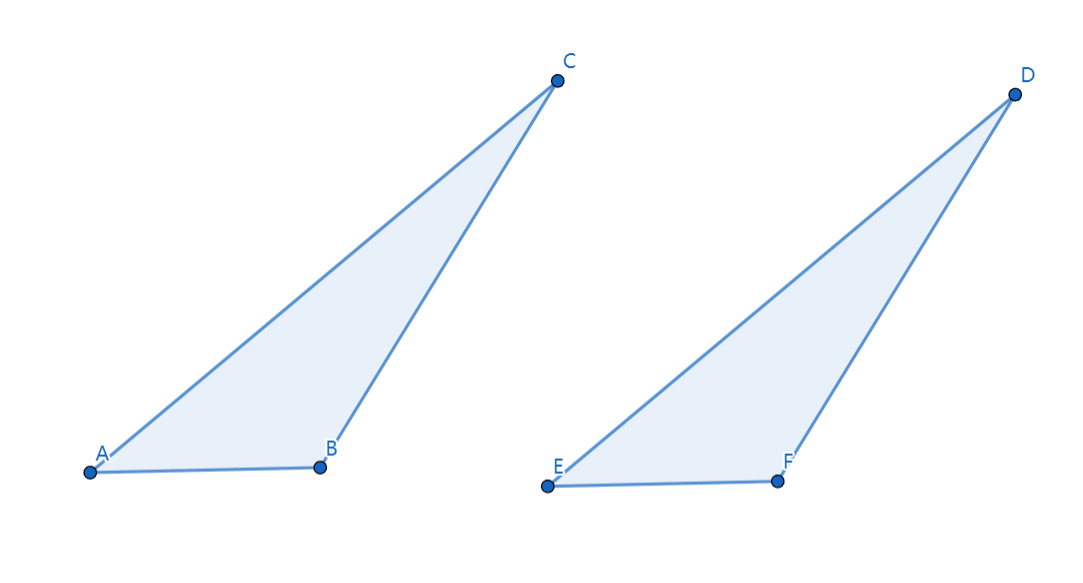
如图，\(AB=EF,AC=DE,∠A=∠E\)

\[∵在△ABC与△DEF中 \\ \begin{cases} AB=EF \\ AC=DE \\ ∠A=∠E \\ \end{cases} \\ ∴△ABC≌△DEF(SAS) \]

两角及一边相等(AAS)

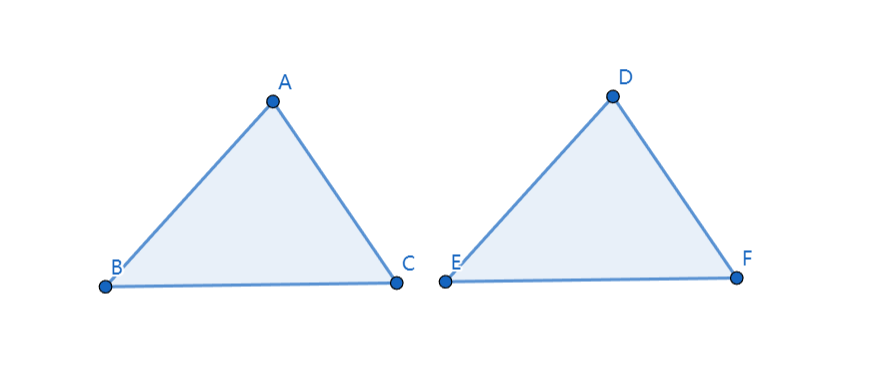
如图，\(BC=EF,∠A=∠D,∠B=∠E\)
则：

\[∵在△ABC与△DEF中 \\ \begin{cases} ∠A=∠D \\ ∠B=∠E \\ BC=EF \\ \end{cases} \\ ∴△ABC≌△DEF(AAS) \]

两角及夹边相等(ASA)

如图，\(∠A=∠D,∠B=∠E,AB=ED\)
则：

\[∵在△ABC与△DEF中 \\ \begin{cases} ∠A=∠D \\ ∠B=∠E \\ AB=ED \\ \end{cases} \\ ∴△ABC≌△DEF(ASA) \]

在\(Rt△\)中，直角边和斜边对应相等(HL)

这个其实相当于SSS，因为勾股定理，直角边与斜边对应相等，那么第三边肯定也是相等的

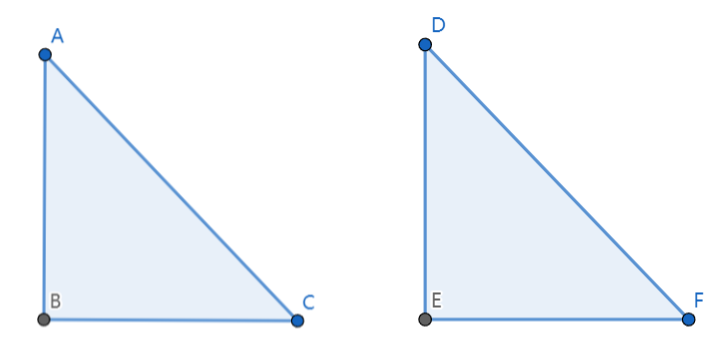
如图：\(AB=DE,AC=DF\)

\[在Rt△ABC和Rt△DEF中\\ \begin{cases} AB=DE\\ AC=DF\\ \end{cases}\\ ∴Rt△ABC≌Rt△DEF(HL) \]

END