浅更道动角例题讲解练练手

写在之前

在上上上上一篇博客中，我们讲解了一道动角问题，也总结了一个公式，但是没有说做题的基本步骤以及注意事项

动角问题做题步骤：

1. 最重要的当然是读题辣！

2. 读完题之后就是我们动角问题最核心的部分：画图
   \(P.S\)在画图时，不必苛求与原题完全一致，可以只将与题目有关的部分画出来，这样子不仅减少了工作量而且可以使我们的思路更加清晰明确

3. 同样也是重要的一环分类讨论
   \(eg.\) 同样的线段旋转，\(OA\)有可能在\(OB\)的左侧，也有可能在\(OB\)的右侧
   分类讨论一定要画图，画图，画图！！！！

例题1

图一是一条直线(MAOBN重合)

(1)

非常简单
公式可以参考之前发过的这篇文章

所以一眼就\(2t\)
还是那个公式

(2)

没有什么实际难度的思维题：
题面中的一句话很重要：第二次

有第二次就有第一次，那么第一次是怎么样的呢？

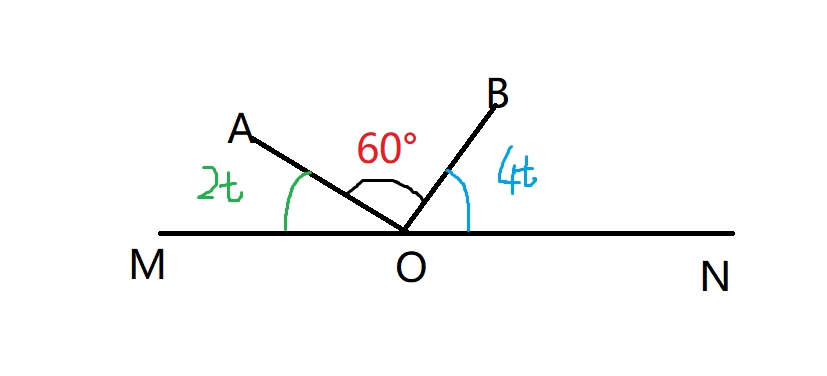
第一次

那么第二次就是OB把OA超了，OB位于OA左侧

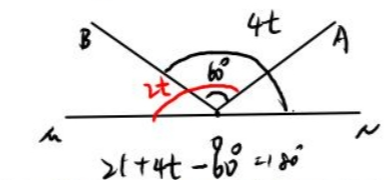
如图，在\(2t+4t\)中，\(60\)已经被算了两次，那我只需要减去多算的就是一个平角了

那么：

\(2t+4t-60=180\)

解得\(t=40\)

(3)

这题我们先写一个\(解:\)代表我们的自信！
其次再写存在，理由如下：
这个时候，你就已经赢了一半了
这真的是我做过最阴间的动角了

射线\(OB\)是\(OM,OA,ON\)其中任意两条直线组成的角的角平分线

这题不难，关键是分类讨论的思路是否正确：

写这种题真的坐牢，愿看到这篇blog的人终生都遇不到这种题

情况一：当\(OB\)平分\(∠AOM\)

画图！

由题可知：\(∠AOM=2t, ∠BON=4t\)
∵ \(OB\)平分\(∠AOM\)
∴ \(∠AOM=2∠BOM=2∠AOB=2t, ∠BOM=∠AOB=t\)
∵ \(∠BOM+∠BON=180\)
∴ \(4t+t=180\) 解得\(t=36\)

情况二：\(OB\)平分\(∠MON\)

因为\(OB\)平分了一个平角，所以\(∠BON=4t=90\)
解就完事
解得\(t=22.5\)

情况三：\(OB\)平分\(∠MON\)但是OB在MN之下

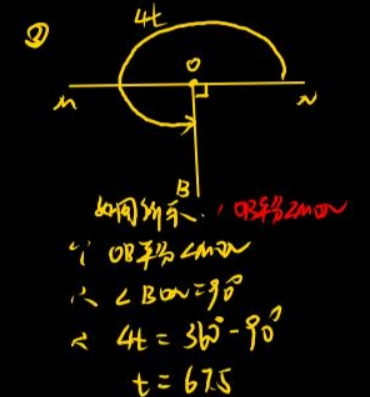
原理类似情况二，不再详细说明

情况四：\(OB\)平分\(∠AON\)

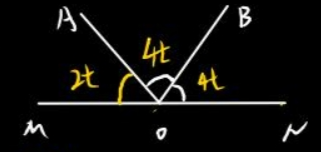
如图所示：
因为\(OB\)平分\(∠AON\)
所以\(∠AON=2∠AOB=8t\)
很显然\(2t+8t=180\)
解得\(t=18\)

综上所述：\(t\)的值为\(36,18,22.5,67.5\)

真是坐牢

// https://img2024.cnblogs.com/blog/3379698/202401/3379698-20240120170046755-1653490543.png

作业：