动点从未如此简单!七上动点问题公式及例题精讲(一)
应某人要求,来浅讲一下数轴动点问题
基本概念:
数字是数字,距离是距离
数字是什么?
数字可正可负,也可是0
如果数轴上有一动点,初始值为,其表示的数为,速度为,设运动时间为
显然,P可以向左运动,也可以向右运动
1.向右,那么可以肯定的是的值必然是随着的运动而增加的,那么增加的就是向右运动的路程
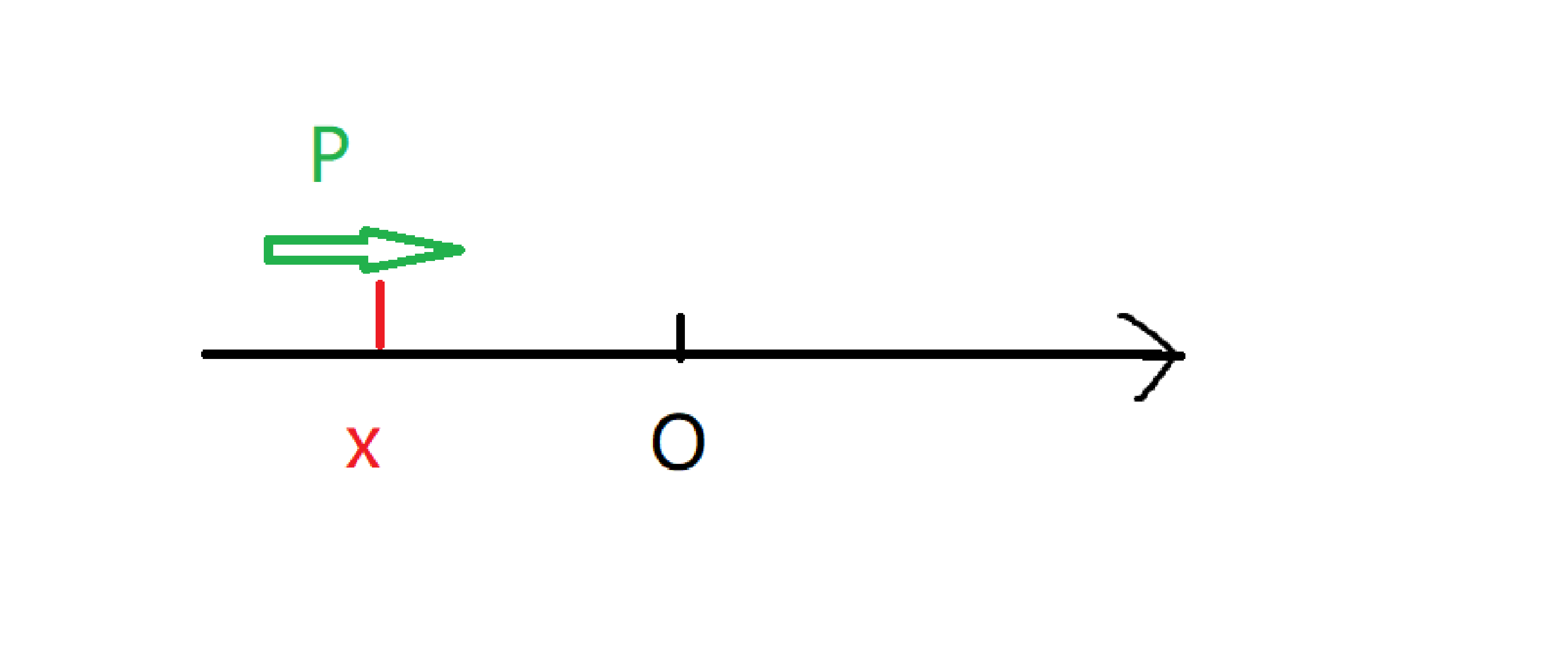
所以:
2.同样的原理,减少的也是
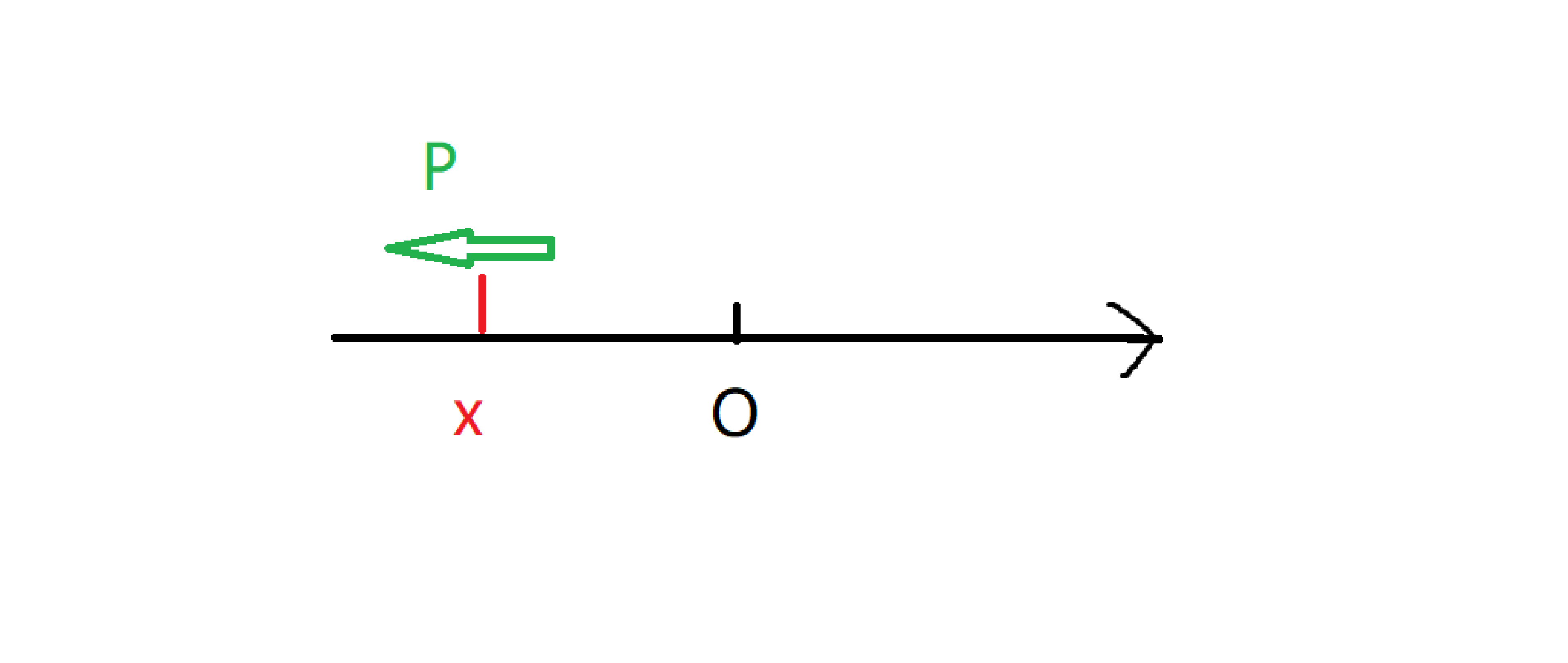
所以:
距离是什么?
距离一定非负
数轴上两点之间的距离表示方法:
- 两点之间左右位置确定: (两点之间的距离右边点表示的数左边点表示的数)
这部分应该很好理解,因为两数位于数轴上正方向(通常为右)的数一定大于负方向(左)的数,其相减就可以得出距离(距离一定非负)
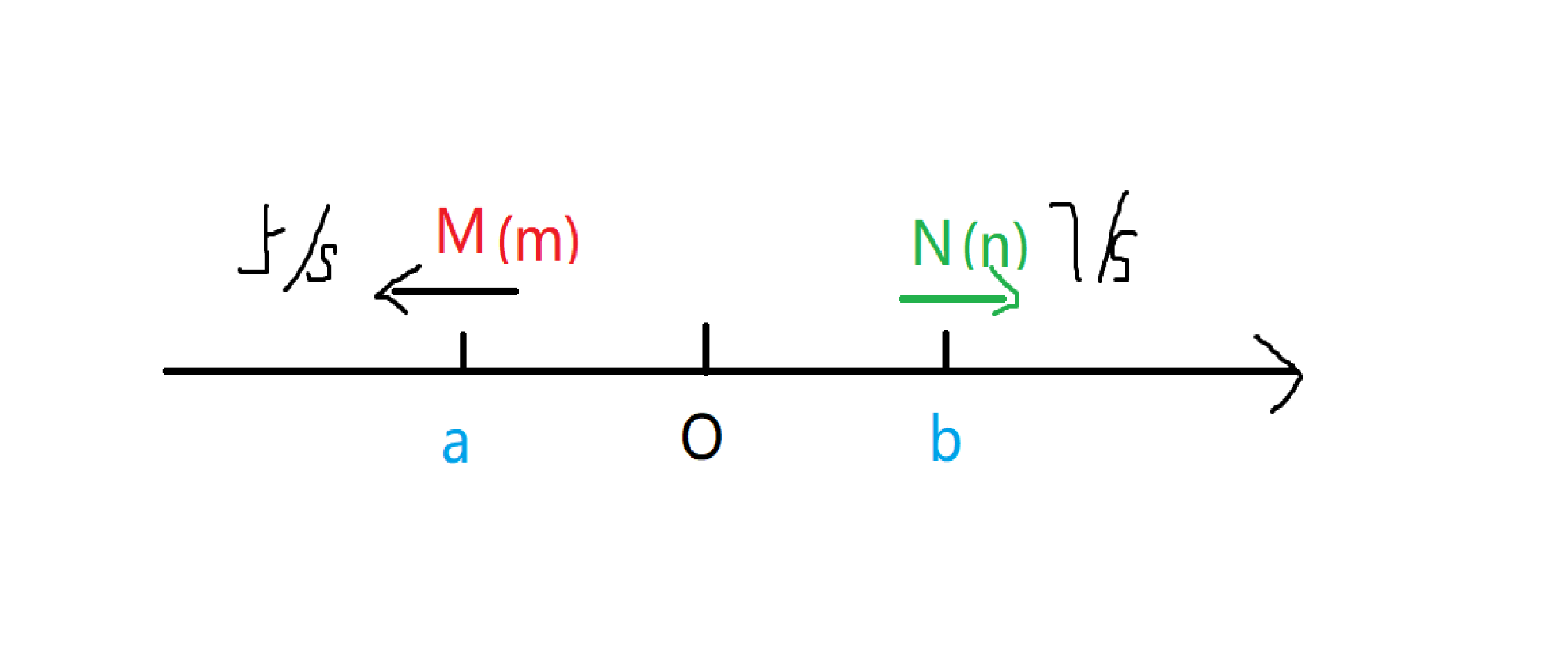
则 距离 右侧的点 - 左侧的点
由已知可得:
所以
- 两点之间左右位置不确定: 或 (两点距离|两点表示之数相减|)
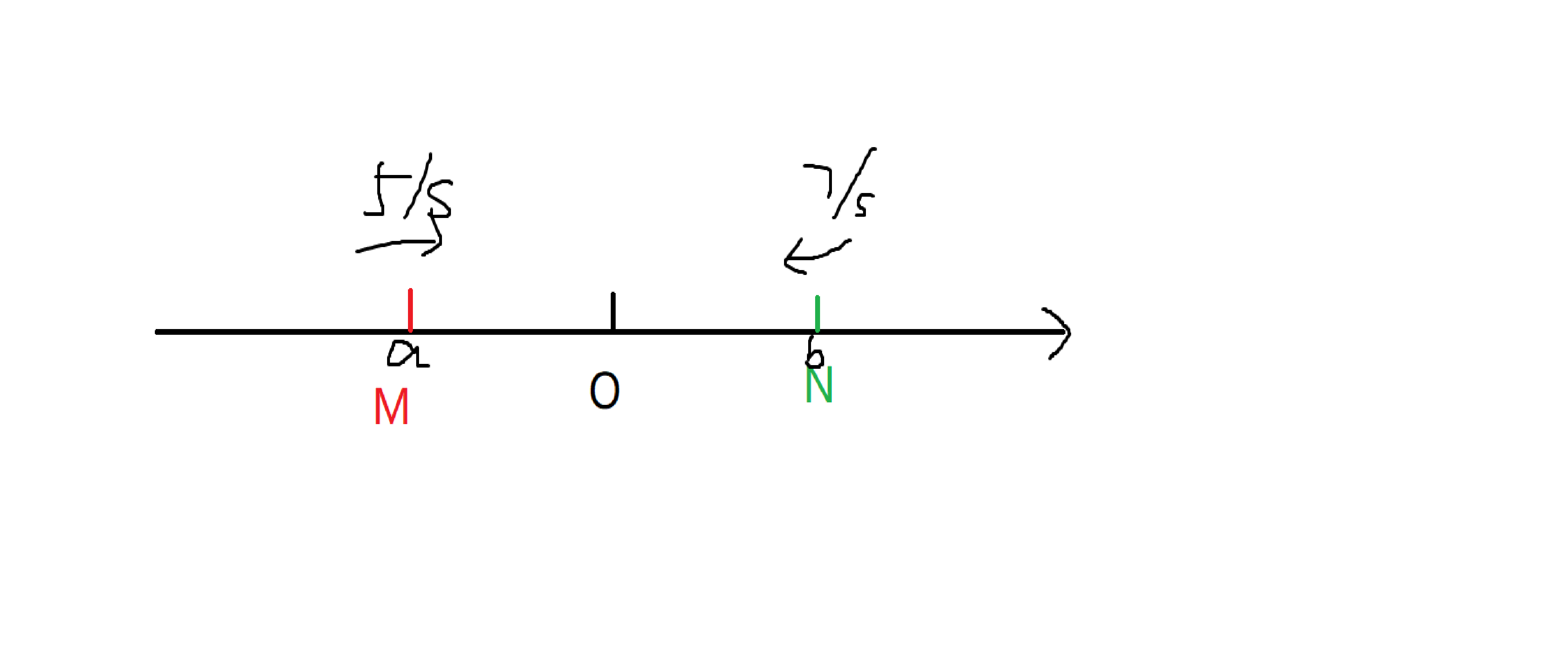
如图:
看图可以知道这两点是相向而行的,那么必然存在多种情况:N位于M右侧、M位于N右侧、M重合于N
∵
∴ 与互为相反数,即,而距离一定非负
恰好满足了绝对值的性质,所以
END
数轴动点的公式其实就是以上这些,但是题目往往会很阴间,所以等我睡一觉再起来发第二篇(例题精讲)
写在结束:写博客是很辛苦的一件事情,这一篇博客的四张插图都是我亲手在电脑里画好上传图床再导入markdown的,所以每一篇博客背后必然是我的付出,希望看到博文的人能够以良好的心态去面对
还有,讲题也并不是一件易事,我需要极其熟悉这个题目的图以及其中蕴含的思想才能流畅的表达出来,拿着答案是无奈之举,你要是觉得你行那行你拿着答案上去给我写8页希沃白板再画两个小时每张插图自己画再写一篇博文试试,you can you up嘛。不想听没人逼你听,就算数学老师讲题也是带答案上去的,语文老师拿的也是教师版书籍。有本事你去在循环两遍月之暗面的时间里去给我写这篇博文。人不行别怪路不平,你不行有的是人行。
——致某个说我没实力还让我知道的人
2024年1月20日00:53:00
还是+v18066864787获取视频版讲解




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现