SPOJ Problem Set (classical)
Most of you have probably tried to type an SMS message on the keypad
of a cellular phone. It is sometimes very annoying to write longer
messages, because one key must be usually pressed several times to
produce a single letter. It is due to a low number of keys on the
keypad. Typical phone has twelve keys only (and maybe some other control
keys that are not used for typing). Moreover, only eight keys are used
for typing 26 letters of an English alphabet. The standard assignment of
letters on the keypad is shown in the left picture:
1
2
3
4
5
6
7
8
9
*
0space
#
1
2
3
4
5
6
7
8
9
*
0space
#
There are 3 or 4 letters assigned to each key. If you want the first
letter of any group, you press that key once. If you want the second
letter, you have to press the key twice. For other letters, the key must
be pressed three or four times. The authors of the keyboard did not try
to optimise the layout for minimal number of keystrokes. Instead, they
preferred the even distribution of letters among the keys.
Unfortunately, some letters are more frequent than others. Some of these
frequent letters are placed on the third or even fourth place on the
standard keyboard. For example, S is a very common letter in
an English alphabet, and we need four keystrokes to type it. If the
assignment of characters was like in the right picture, the keyboard
would be much more comfortable for typing average English texts.
ACM have decided to put an optimised version of the keyboard on its
new cellular phone. Now they need a computer program that will find
an optimal layout for the given letter frequency. We need to preserve
alphabetical order of letters, because the user would be confused if the
letters were mixed. But we can assign any number of letters to a single
key.
Input
There is a single positive integer T on the first line of
input (equal to about 2000). It stands for the number of test cases to
follow. Each test case begins with a line containing two integers K , L (1 <= K <= L <= 90) separated by a single space. K is the number of keys, L is the number of letters to be mapped onto those keys. Then there are two lines. The first one contains exactly K characters each representing a name of one key. The second line contains exactly L characters
representing names of letters of an alphabet. Keys and letters are
represented by digits, letters (which are case-sensitive), or any
punctuation characters (ASCII code between 33 and 126 inclusively). No
two keys have the same character, no two letters are the same. However,
the name of a letter can be used also as a name for a key.
After those two lines, there are exactly L lines each containing exactly one positive integer F 1 , F 2 , ... F L
Output
Find an optimal keyboard for each test case. Optimal keyboard is such that has the lowest "price" for typing average text. The price is determined as the sum of the prices of each letter. The price of a letter is a product of the letter frequency (F i
If there are more solutions with the same price, we will try to
maximise the number of letters assigned to the last key, then to the one
before the last one etc.
More formally, you are to find a sequence P 1 , P 2 , ... P L
P 1 = 1for each i >1, either P i P i -1P i
there are at most K numbers P i P i
the sum of products S P F i P i
for any other sequence Q meeting these criteria and with the same sum S Q S P M , 1 <= M <= L that for any J , M <J <= L , P J Q J P M Q M
The output for every test case must start with a single line saying Keypad # I : , where I is a sequential order of the test case, starting with 1. Then there must be exactly K lines,
each representing one letter, in the same order that was used in input.
Each line must contain the character representing the key, a colon, one
space and a list of letters assigned to that particular key. Letters
are not separated from each other.
Print one blank line after each test case, including the last one.
Example
Sample Input:
1
8 26
23456789
ABCDEFGHIJKLMNOPQRSTUVWXYZ
3371
589
1575
1614
6212
971
773
1904
2989
123
209
1588
1513
2996
3269
1080
121
2726
3083
4368
1334
518
752
427
733
871
Sample Output:
Keypad #1:
2: ABCD
3: EFG
4: HIJK
5: LM
6: NOPQ
7: RS
8: TUV
9: WXYZ
Warning: large Input/Output data, be careful with certain languages
Added by:
Adrian Kosowski
Date:
2004-05-09
Time limit:
5s
Source limit:
50000B
Languages:
All
Resource:
ACM Central European Programming Contest, Prague 2000
这道题目是说使用手机上的数字小键盘发送短信的话,有些英文字母需要多次按同一个数字键才能输入。比如很常用的字母“s”就需要按四次“7”键才 行。我们的任务是写一个程序,在不改变字母的顺序的情况下,将这些字母分配到各个按键上,使用得输入信息的总的按键次数最少。输入信息中各个字母出现的频 率是已经给定的。
问题解答
下面就是使用动态规划算法 解答的 C 语言源程序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <stdio.h>
#include <string.h>
#define MAX (90 + 1)
static int cost[MAX][MAX], price[MAX][MAX], index[MAX][MAX];
void initialize(int L, int F[])
{
memset(price, 0x40, sizeof(price));
price[0][0] = 0;
for (int i = 1; i <= L; i++)
for (int j = i; j <= L; j++)
cost[i][j] = cost[i][j - 1] + (j - i + 1) * F[j - 1];
}
void compute(int K, int L)
{
for (int i = 1; i <= K; i++)
for (int j = i; j <= L; j++)
for (int n = 1; n <= j - i + 1; n++)
{
int sum = price[i - 1][j - n] + cost[j - n + 1][j];
if (sum <= price[i][j]) price[i][j] = sum, index[i][j] = n;
}
}
void output(int K, int L, char keys[], char letters[])
{
if (K == 0) return;
output(K - 1, L - index[K][L], keys, letters);
printf("%c: ",keys[K - 1]);
for (int i = L - index[K][L]; i < L; i++) putchar(letters[i]);
puts("");
}
int main(void)
{
int F[MAX - 1], T;
scanf("%d", &T);
for (int K, L, n = 1; n <= T; n++)
{
char keys[MAX], letters[MAX];
scanf("%d%d%s%s", &K, &L, keys, letters);
for (int i = 0; i < L; i++) scanf("%d", F + i);
initialize(L, F);
compute(K, L);
printf("Keypad #%d:\n", n);
output(K, L, keys, letters);
puts("");
}
return 0;
}
假设我们有以下输入:
1
3 9
123
ABCDEFGHI
1
30
10
10
10
31
11
12
9
运行该程序将得到以下输出:
Keypad #1:
1: A
2: BCDE
3: FGHI
算法分析
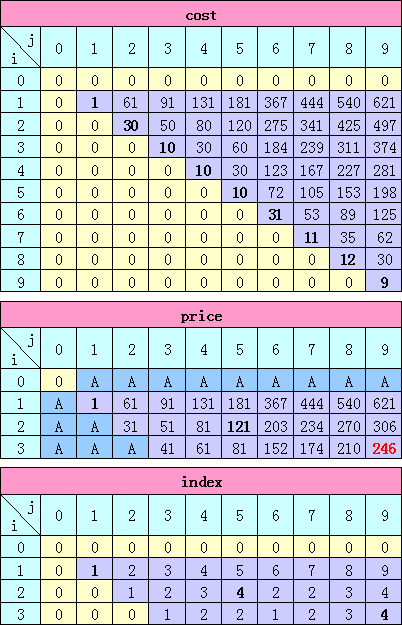
使用上一节的输入数据运行该程序,主要的运行状态如下所示:
上述程序中:
K 是按键的个数。L 是要分配到各个按键中的字符的个数。T 是测试案例的个数。一维数组 F 的大小为 L,保存各个字符出现的频率。
cost 是大小为 L x L 的二维数组,cost[i][j] 表示第 i 到第 j 个字符分配到某个按键上的代价,即输入这 j - i + 1 个字符(乘上它们出现的频率)的总的按键次数。注意,主对角线上的值就是各个字符出现的频率。这体现在源程序中 initialize 函数的第 12 到第 14 行。初始化之后,cost 的数组的值就不再改变了。
price 是大小为 K x L 的二维数组,price[i][j] 表示前 j 个字符分配在前 i 个按建上的最小代价。上图中的 A 的值是大约是 INT_MAX 的一半。第一个字符一定是分配在第一个按键上的,而不管第一个字符出现的频率如何(实际上第一个字符的频率可以设置为任何正数,而不影响程序的运行结 果)。所以 price[0][0] 初始化设置为 0,而 price 数组的其他值初始化为一个比较大的数。
index 是大小为 K x L 的二维数组,index[K][L] 表示第 K 个(最后一个)按键上分配的字符数,然后往回倒算,index[K - 1][L - index[K][L]] 表示第 K - 1 个按键上分配的字符数,... 一直倒算到第 1 个按键为止。这体现在源程序第 28 到 35 行的 output 函数中,使用递归是为了以正确的顺序输出这些按键。
程序中最关键的是第 17 到第 26 行的 compute 函数。该函数通过三重循环将问题分角为子任务用动态规划算法求解。子任务是求将 j 个字符分配到 i 个按键上的最小代价。
第 19 行:i 从 1 到 K 循环逐步求解。总共有 K 个按键。
第 20 行:j 从 i 到 L 循环逐步求解。总共有 L 个字符,且每个按键至少必须分配一个字符。
第 21 行:n 从 1 到 j - i + 1 逐步求解。注意,这里 n 是指最后一个按键中分配的字符数。
第 23 行:这是最关键的计算最小代价的公式,sum 由两部分组成,第二部分是将第 j - n + 1 到第 j 个字符(总共 n 个)分配到第 i 个按键(也就是该子任务中的最后一个按键)中的最小代价,第一部分就是将该子任务中剩下的 j - n 个字符分配到前 i - 1 个按键中的最小代价。注意,该子任务总共要分配 j 个字符。
第 24 行:如果计算出来的最小代价比原来的小,就更新最小代价数组 price,并同时更新 index 数组,以便将来输出键盘布局。
三重循环完成,表明整个计算任务完成,L 个字符已经分配到 K 个按键中。此时,price[K][L] 表示所求的最小代价,在我们例子中就是 246。
注意,这道题目要求在同等代价下将字符尽量分配到后面的按键中,所以第 24 行比较代价时使用“<=”,以便尽量增加后面按键的字符数。 如果将这个程序第 24 行的“<=”改为“<”,则将得到以下输出:
Keypad #1:
1: ABC
2: DE
3: FGHI
此时,策略是在同等代价下将字符尽量分配到前面的按键中。
英语国家手机数字键盘的最优方案
维基百科网站的 Letter frequency 给出了英语中二十六个字母出现的频率,如下表所示:
Letter Frequency
a 8.167%
b 1.492%
c 2.782%
d 4.253%
e 12.702%
f 2.228%
g 2.015%
h 6.094%
i 6.966%
j 0.153%
k 0.772%
l 4.025%
m 2.406%
n 6.749%
o 7.507%
p 1.929%
q 0.095%
r 5.987%
s 6.327%
t 9.056%
u 2.758%
v 0.978%
w 2.360%
x 0.150%
y 1.974%
z 0.074%
根据上表设置相应的输入文件:
1
8 26
23456789
ABCDEFGHIJKLMNOPQRSTUVWXYZ
8167
1492
2782
4253
12702
2228
2015
6094
6966
153
772
4025
2406
6749
7507
1929
95
5987
6327
9056
2758
978
2360
150
1974
74
运行结果如下所示:
Keypad #1:
2: AB
3: CD
4: EFG
5: HIJK
6: LM
7: NOPQ
8: RS
9: TUVWXYZ
数字“9”键上居然有七个英文字母,可见最后几个英文字母出现的频率很低。看来在英文国家手机的数字键盘应该如上设置才能够更好地输入信息。当然, 我们输入中文又是另外一回事了,用拼音和用五笔输入法,各个字母的频率也是不同的。其实手机向智能化发展,越来越多地使用全键盘了,不再使用数学小键盘。