【转载】高斯概率密度函数

1.单变量正态分布

单变量正态分布概率密度函数定义为： $$\Large{p(x) = \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{1}{2}{{(\frac{{x - \mu }}{\sigma })}^2}}}}$$

其中，μ为随机变量x的期望，${\sigma ^2}$为x的方差，${\sigma}$为x的标准差。

$\$\$\backslash Large\backslash mu\; =\; E(x)\; =\; \backslash int\_\{\; -\; \backslash infty\; \}^\backslash infty\; \{xp(x)dx\}\$\$$

$\$\$\backslash Large\{\backslash sigma\; ^2\}\; =\; \backslash int\_\{\; -\; \backslash infty\; \}^\backslash infty\; \{\{\{(x\; -\; \backslash mu\; )\}^2\}\}\; p(x)dx\$\$$

 

$matlab绘制正态分布曲线：$

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

% 绘制单变量正态分布概率密度曲线 x1=-5:0.01:5; % 注意取值的对称性 subplot(2,1,1) % subplot(m,n,p):m和n代表在一个图像窗口中显示m行n列个图像，p代表现在选定第p个图像区域 % normpdf:正态概率密度函数。Y=normpdf(X,mu,sigma),mu:均值,sigma:标准差,Y:正态概率密度函数在x处的值 y1=normpdf(x1,0,1); plot(x1,y1,'r'); title('\mu=0,\sigma^2=1') xlabel('x') ylabel('\rho(x)') subplot(2,1,2) x2=-5:0.01:7; % 注意取值的对称性 y2=normpdf(x2,1,sqrt(0.2)); plot(x2,y2,'r'); title('\mu=1,\sigma^2=0.2') xlabel('x') ylabel('\rho(x)')

 可视化：

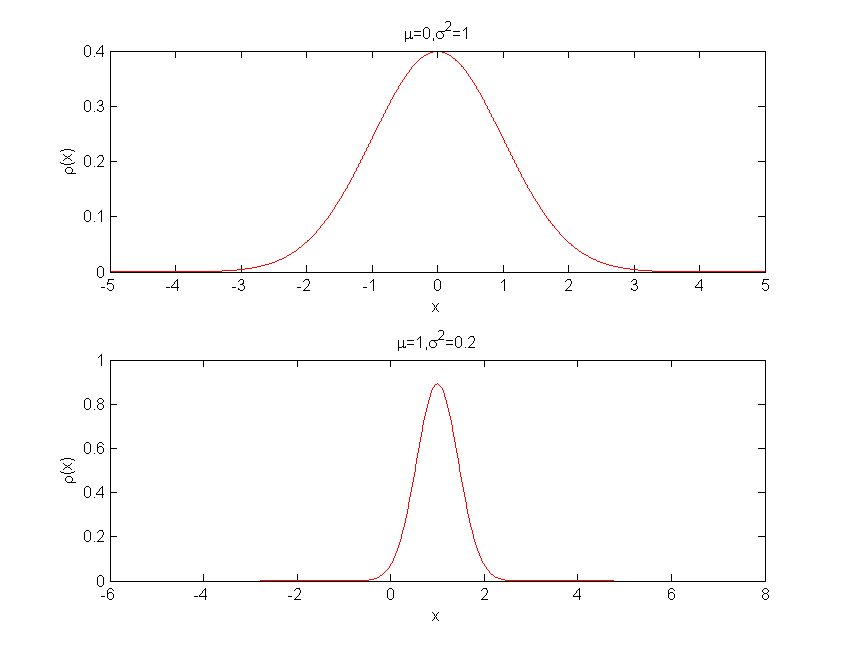
由图中可知，方差越大曲线越宽，曲线始终以$\mu$为中心

2.多元正态分布

（1）多元正态分布的概率密度函数的定义为：

$\$\$\backslash Large\; p(x)\; =\; \backslash frac\{1\}\{\{\{\{(2\backslash pi\; )\}^\{d/2\}\}|\backslash sum\; \{|^\{1/2\}\}\}\}\backslash exp\; [\; -\; \backslash frac\{1\}\{2\}\{(x\; -\; \backslash mu\; )^T\}\{\backslash sum\; ^\{\; -\; 1\}\}(x\; -\; \backslash mu\; )]\$\$$

式中：$x = {[{x_1},{x_2}, \ldots ,{x_d}]^T}$是d维列向量；$\mu  = {[{\mu _1},{\mu _2}, \ldots ,{\mu _d}]^T}$是d维均值向量；$\sum$是d x d维协方差矩阵，${\sum ^{ - 1}}$是$\sum$的逆矩阵，${|\sum |}$是$\sum$的行列式。

定义$\sum$为：

$$\Large\sum {\rm{ = E}}[(x - \mu ){(x - \mu )^T}]$$

显然，d=1时，多变量高斯与单变量高斯一致。有时用符号$N(\mu ,\sum )$表示均值为$\mu$、协方差为$\sum$的高斯概率密度函数。

为了更好地理解什么是多变量高斯，我们考虑在二维空间的一些情况，二维空间是可视的。在这种情况下，有：

$$\Large \sum  = \left( {\begin{array}{*{20}{c}} {{\sigma _1}^2}&{{\sigma _{12}}}\\ {{\sigma _{21}}}&{{\sigma _2}^2} \end{array}} \right)$$

其中$(x - \mu )$为2×1的列向量，${(x - \mu )^T}$为1×2的行向量。对于每个${\mu _i}$有$E({x_i}) = {\mu _i},i = 1,2$，通过定义${\sigma _{12}} = E[({x_1} - {\mu _1})({x_2} - {\mu _2})]$，得到随机变量${x_1}$和${x_2}$的协方差，这个可以度量它们的相互统计相关性。在统计意义下，如果变量是独立的，其协方差为0。显然，$\sum$对角元素是随机向量中各个元素的方差。

2.二维高斯概率密度函数的示例

 代码：

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

% 绘制双变量正态分布概率密度曲线 x = 1 : 0.3 : 7; y = 1 : 0.3 : 7; % 生成网络矩阵 [X,Y]=meshgrid(x,y); U1 = 4.0; % X的均值 DX = 1; % X的方差 dx = sqrt(DX); U2 = 3.8; % Y的均值 DY = 1; % Y的方差 dy = sqrt(DY) COV = 0; % X Y的协方差 % X和Y的相关系数 r = COV / (dx * dy); part1 = 1 / (2 * pi * dx * dy * sqrt(1-r^2)); p1 =  -1 / (2 * (1 - r^2)); px = (X-U1).^2 ./ DX; py = (Y-U2).^2 ./ DY; pxy = 2 * r .* (X-U1) .* (Y-U2) ./ (dx * dy); Z = part1 * exp(p1 * (px - pxy + py)); figure(1) mesh(X,Y,Z) xlabel('x1'); ylabel('x2'); zlabel('\rho(x)'); title('二维概率密度曲线'); figure(2); mesh(X,Y,Z); xlabel('x1'); ylabel('x2'); zlabel('\rho(x)'); title('等值曲线'); % 设置视点的函数 view(0,90);

 3.1 ${\sigma _1}^2 = {\sigma _2}^2$

 

二维概率密度函数曲线：

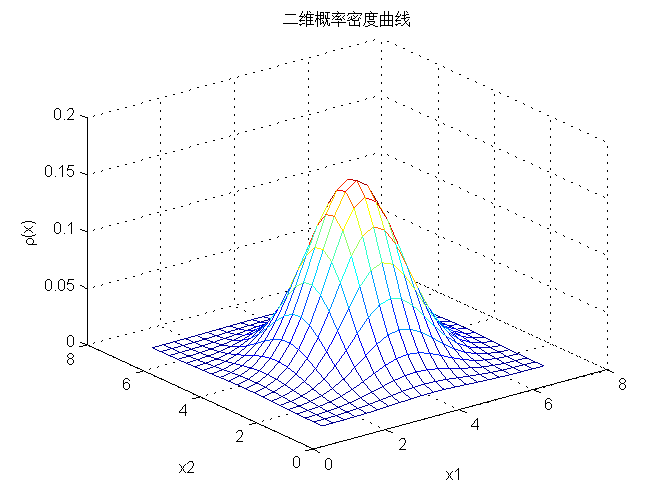
等值曲线：

 

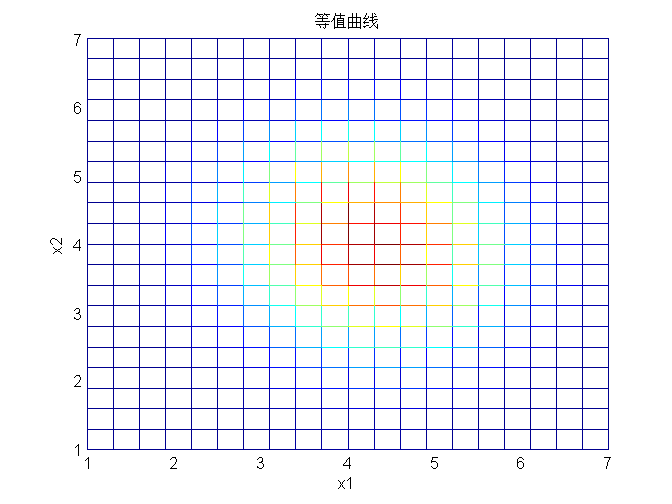
 3.2 ${\sigma _1}^2  >>  {\sigma _2}^2$

(DX=16,DY=4)

二维概率密度函数曲线：

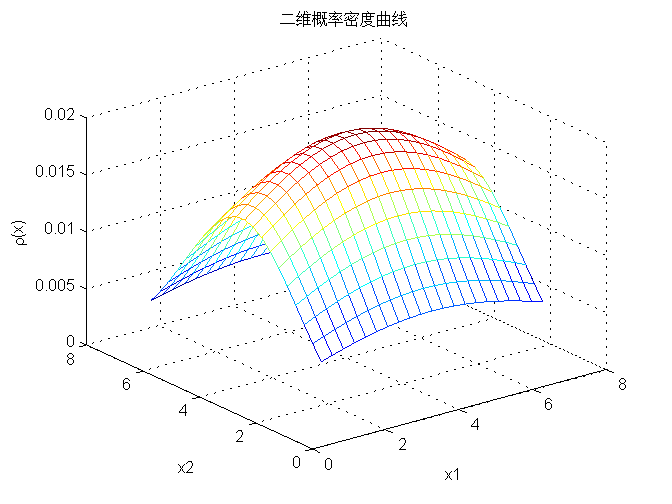
等值曲线：

 

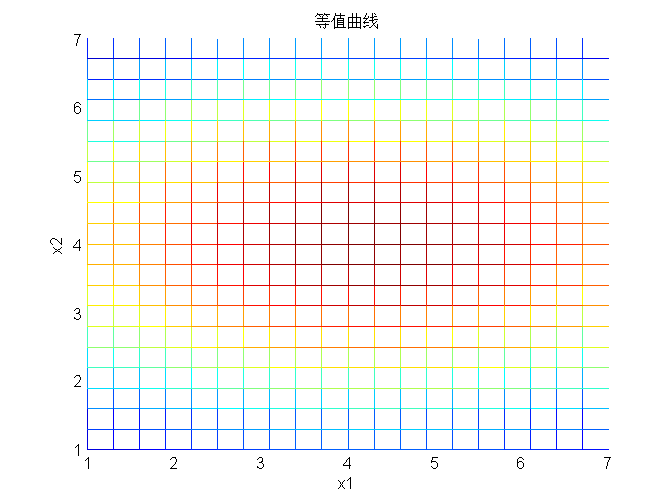
此时等值曲线呈现向x1方向延伸状。

3.3 ${\sigma _2}^2 >  > {\sigma _1}^2$

(DX=4,DY=16)

二维概率密度函数曲线：

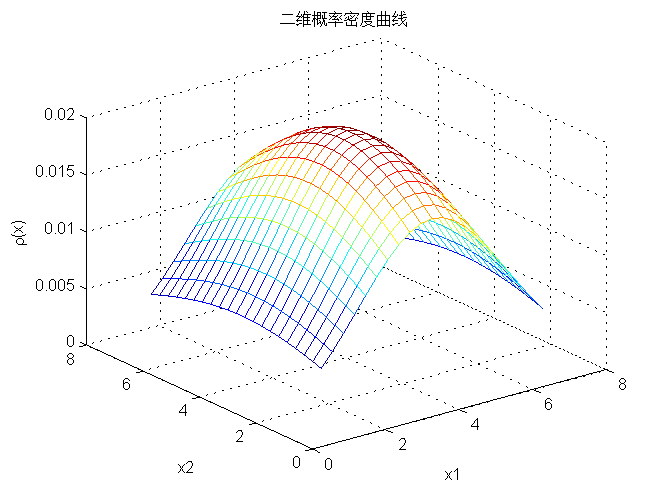
等值曲线：

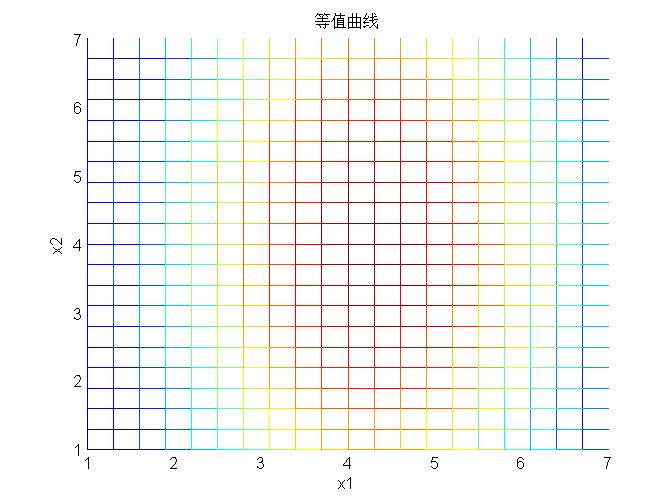
此时等值曲线呈现向x2​方向延申状。

3.4 ${\sigma _{12}} \ne 0$

(U1 = 4.0,DX = 16,U2 = 3.8,DY = 4,COV = 4)

二维概率密度函数曲线：

 

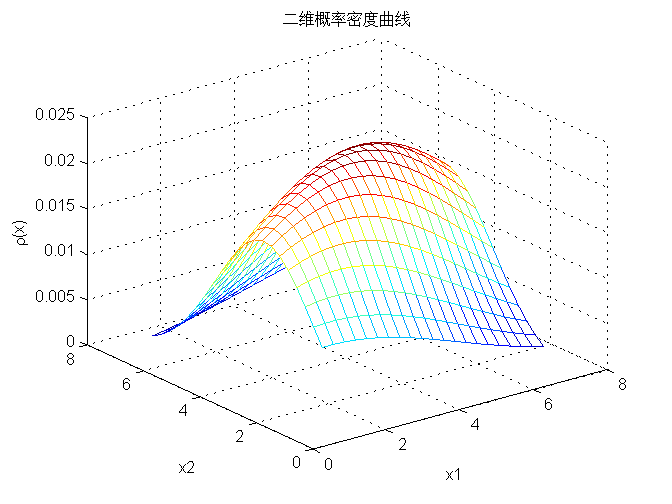
等值曲线：

 

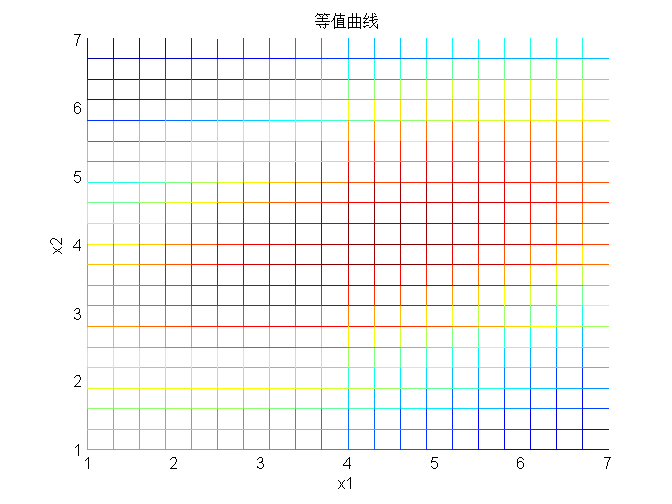
由于改变 ${\sigma _1}^2,{\sigma _2}^2,{\sigma _{12}}$​的值就可以得到不同的形状和方向。
等值曲线是不同方向、与短轴长度成不同比例的椭圆。考虑对角线协方差矩阵的随机向量的均值为0，即${\mu _1} = 0,{\mu _2} = 0$，即有如下方程：（计算等值曲线相当于计算指数为常数$C$的曲线）

$$\frac{{{x_1}^2}}{{{\sigma _1}^2}} + \frac{{{x_2}^2}}{{{\sigma _2}^2}} = C$$

 

附：

二维高斯分布计算公式：

 

原文链接：https://blog.csdn.net/linjing_zyq/article/details/120364622

参考：https://baike.baidu.com/item/%E4%BA%8C%E7%BB%B4%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83/2951835?fr=aladdin