数独问题的规则是:
在9×9的格子中,用1到9共9个阿拉伯数字填满整个格子,其中的一些格子给定初始值,填充其他格子,要求符合:
- 1. 每一行都用到1,2,3,4,5,6,7,8,9,位置不限;
- 2.每一列都用到1,2,3,4,5,6,7,8,9,位置不限;
- 3.每3×3的格子都用到1,2,3,4,5,6,7,8,9,位置不限(图中粗线分开的小区域);
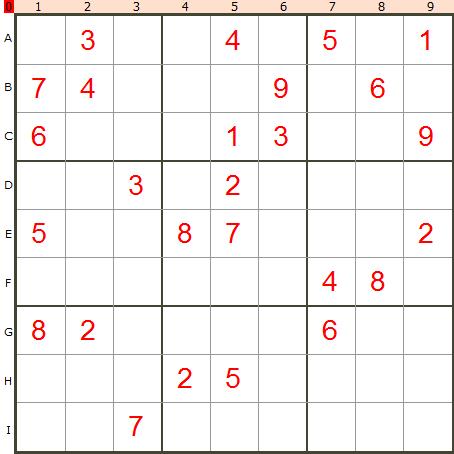
使用递归也可以相对简单的解决这个问题。不过不使用递归来自己考虑各种回溯的问题比较锻炼思维,下面是我自己创建栈然后使用回溯法解决这个问题的方案下面来看我的代码,代码中已经给出了详细的注释:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace GameMath
{
class Program
{
static void Main(string[] args)
{
DateTime time1 = DateTime.Now;
GameMath gm = new GameMath();
gm.Intial();
gm.Creat();
DateTime time2 = DateTime.Now;
Console.WriteLine(time2 - time1);
}
}
class GameMath
{
private int[,] map;
private Stack<StackContent> mapStack;//用来保存数组状态的栈
private List<int[,]> resuleMap;//用来保存正确的数独结果的List
public void Intial()
{
mapStack = new Stack<StackContent>();
resuleMap = new List<int[,]>();
//初始化数组
map=new int[10,10];
for (int i = 1; i <= 9; i++)
{
for (int j = 1; j <= 9; j++)
{
map[i,j] = 0;
}
}
map[1, 1] = 5; map[1, 2] = 3; map[2, 2] = 1; map[3, 3] = 9; map[2, 4] = 7;
map[2, 5] = 2; map[3, 6] = 6; map[2, 8] = 8; map[3, 8] = 3; map[4, 2] = 9;
map[4, 3] = 7; map[5, 1] = 3; map[5, 2] = 2; map[4, 4] = 6; map[5, 5] = 4;
map[6, 5] = 5; map[4, 9] = 3; map[6, 9] = 2; map[8, 3] = 4; map[7, 4] = 4;
map[9, 5] = 3; map[7, 7] = 2; map[9, 8] = 1;
}
//产生数独的算法
public void Creat()
{
for (int i = 1; i <= 9; i++)
{
for (int j = 1; j <= 9; j++)
{
//如果该单元格已经有初始值,则跳过
if (map[i, j] != 0)
{
continue;
}
for (int num = 1; num <= 9; num++)
{
//如果合法,则放入数
if (Valid(i, j, num))
{
map[i, j] = num;
//合法状态压入状态栈
StackContent sc = new StackContent(i, j, map);
mapStack.Push(sc);
if (i == 9 && j == 9)
{
//此时,整个数组填完,到达终态,找到一个合法的
PrintResult();
Console.WriteLine();
//将该合法的结果存入结果List中
int[,] validMap = new int[10, 10];
for (int i1 = 1; i1 <= 9; i1++)
{
for (int j1 = 1; j1 <= 9; j1++)
{
validMap[i1, j1] = map[i1, j1];
}
}
resuleMap.Add(validMap);
//状态栈回退,将当前状态回退到以前的状态,找其他的合法终态
if (mapStack.Count != 0)
{
StackContent oldersc = mapStack.Pop();
i = oldersc.i;
j = oldersc.j;
map = oldersc.map;
num = map[i, j];
map[i, j] = 0;
}
//如果回退后状态无法继续进行,则回退到可以为止
while (num == 9)
{
if (mapStack.Count != 0)
{
StackContent oldersc = mapStack.Pop();
i = oldersc.i;
j = oldersc.j;
map = oldersc.map;
num = map[i, j];
map[i, j] = 0;
}
else
{
return;
}
}
//////////////////////////////////////////////////
}
//与if (i == 9 && j == 9)对应,没有到达终态时,继续往下填数
else
{
break;
}
}
else
{
//该位置数字1到9都不合法,说明上一个状态也不对,回退重新生成上一状态
while (num == 9)
{
if (mapStack.Count != 0)
{
StackContent oldersc = mapStack.Pop();
i = oldersc.i;
j = oldersc.j;
map = oldersc.map;
num = map[i, j];
map[i, j] = 0;
}
else
{
return;
}
}
}
}
}
}
}
//判断在一个单元格中放入数是否合法
public bool Valid(int i, int j, int num)
{
//判断同一行中
for (int jj = 1; jj <= 9; jj++)
{
if (map[i, jj] == num)
{
return false;
}
}
//判断同一列中
for (int ii = 1; ii <= 9; ii++)
{
if (map[ii, j] == num)
{
return false;
}
}
//判断其所在的单元格中
for (int ii = ((i-1 )/ 3 )*3+ 1; ii <= ((i-1 )/ 3)*3 + 3; ii++)
{
for (int jj = ((j-1) / 3)*3 + 1; jj <= ((j-1 )/ 3)*3 + 3; jj++)
{
if (map[ii,jj] == num)
{
return false;
}
}
}
//判断当前状态是否已经是存入结果中的,如果已经存在,则视为不合法,避免重复
if (i == 9 && j == 9)
{
return !AlreadyInResultList();
}
return true;
}
//判断当前状态是否已经是存入结果List中
public bool AlreadyInResultList()
{
bool equal = false;
foreach (int[,] result in resuleMap)
{
//遍历结果List,判断当前状态是否已存入该List
equal = true;
for (int i = 1; i <= 9; i++)
{
for (int j = 1; j <= 9; j++)
{
if(map[i,j]!=result[i,j])
{
equal = false;
break;
}
}
if (!equal)
{
break;
}
}
if(equal)
{
return true;
}
}
return equal ;
}
//打印结果
public void PrintResult()
{
for (int i = 1; i <= 9; i++)
{
for (int j = 1; j <= 9; j++)
{
Console.Write(map[i, j] + " ");
}
Console.WriteLine();
}
}
//数组状态栈中保存的节点类
class StackContent
{
public int i{get;set;}
public int j { get; set; }
public int[,] map { get; set; }
public StackContent(int i, int j, int[,] externalMap)
{
this.i = i;
this.j = j;
map = new int[10, 10];
for (int i1 = 1; i1 <= 9; i1++)
{
for (int j1 = 1; j1 <= 9; j1++)
{
this.map[i1, j1] = externalMap[i1, j1];
}
}
}
}
}
}
////////////////////////////////////////////////////////////////////////////
附注: 数独问题的递归解法
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace shudu
{
class Program
{
static int[,] cube = new int[10, 10];
static int count;
static void initial()
{
for (int i = 1; i <= 9; i++)
{
for (int j = 1; j <= 9; j++)
{
cube[i, j] = 0;
}
}
cube[1, 1] = 5;
cube[1, 2] = 3;
cube[2, 2] = 1;
cube[3, 3] = 9;
cube[2, 4] = 7;
cube[2, 5] = 2;
cube[3, 6] = 6;
cube[2, 8] = 8;
cube[3, 8] = 3;
cube[4, 2] = 9;
cube[4, 3] = 7;
cube[5, 1] = 3;
cube[5, 2] = 2;
cube[4, 4] = 6;
cube[5, 5] = 4;
cube[6, 5] = 5;
cube[4, 9] = 3;
cube[6, 9] = 2;
cube[8, 3] = 4;
cube[7, 4] = 4;
cube[9, 5] = 3;
cube[7, 7] = 2;
cube[9, 8] = 1;
}
static bool tryshudu(int i, int j, int num)
{
cube[i, j] = num;
for (int temp = 1; temp <= 9; temp++)
{
if (cube[i, j] == cube[i, temp] && j != temp)
{
return false;
}
if (cube[i, j] == cube[temp, j] && i != temp)
{
return false;
}
}
int cubex = ((i - 1) / 3) * 3 + 1;
int cubey = ((j - 1) / 3) * 3 + 1;
int temp1 = cubex;
int temp2 = cubey;
int xmax = cubex + 2;
int ymax = cubey + 2;
for (cubex = temp1; cubex <= xmax; cubex++)
{
for (cubey = temp2; cubey <= ymax; cubey++)
{
if (cube[cubex, cubey] == cube[i, j] && (i != cubex || j != cubey))
{
return false;
}
}
}
return true;
}
static bool allok()
{
for (int i = 1; i <= 9; i++)
{
for (int j = 1; j <= 9; j++)
{
if (cube[i, j] == 0)
return false;
}
}
return true;
}
static void print()
{
for (int i = 1; i <= 9; i++)
{
for (int j = 1; j <= 9; j++)
{
Console.Write(cube[i, j] + " ");
}
Console.WriteLine();
}
Console.WriteLine();
}
static void shudu(int x, int y)
{
if (x > 9 || y > 9)
return;
if (cube[x, y] == 0 )
{
for (int num = 1; num <= 9; num++)
{
if (tryshudu(x, y, num))
{
if (allok())
{
print();
count++;
}
else
{
if (y >= 9)
shudu(x + 1, 1);
else
shudu(x, y + 1);
}
}
}
cube[x, y] = 0;
}
else
{
if (y >= 9)
shudu(x + 1, 1);
else
shudu(x, y + 1);
}
}
static void Main(string[] args)
{
initial();
DateTime dd = DateTime.Now;
shudu(1, 1);
Console.WriteLine(count);
DateTime d2 = DateTime.Now;
Console.WriteLine(d2 - dd);
}
}
}




