一、种类介绍
算术表达式有三种:前缀表达式、中缀表达式和后缀表达式。一般用的是中缀,比如1+1,前后缀就是把操作符移到前面和后面,下面简单介绍一下这三种表达式。
1、前缀表示法
前缀表示法又叫波兰表示法,他的操作符置于操作数的前面(例:+ 1 2),是波兰数学家扬·武卡谢维奇1920年代引入的,用于简化命题逻辑。因为我们一般认为操作符是在操作数中间的,所以在日常生活中用的不多,但在计算机科学领域占有一席之地。一般的表示法对计算机来说处理很麻烦,每个符号都要考虑优先级,还有括号这种会打乱优先级的存在,将使计算机花费大量的资源进行解析。而前缀表示法没有优先级的概念,他是按顺序处理的。举个例子:9-2*3这个式子,计算机需要先分析优先级,先乘后减,找到2*3,再进行减操作;化成前缀表示法就是:- 9 * 2 3,计算机可以依次读取,操作符作用于后一个操作数,遇到减就是让9减去后面的数,而跟着9的是乘,也就是说让9减去乘的结果,这对计算机来说很简单,按顺序来就行了。
2、中缀表示法
这也就是我们一般的表示法,他的操作符置于操作数的中间(例:1 + 2),前面也说过这种方法不容易被计算机解析,但他符合人们的普遍用法,许多编程语言也就用这种方法了。在中缀表示法中括号是必须有的,要不然运算顺序会乱掉。
3、后缀表示法
后缀表示法又叫逆波兰表示法,他的操作符置于操作数的后面(例:1 2 +),他和前缀表示法都对计算机比较友好,但他很容易用堆栈解析,所以在计算机中用的很多。
他的解释过程一般是:操作数入栈;遇到操作符时,操作数出栈,求值,将结果入栈;当一遍后,栈顶就是表达式的值。因此逆波兰表达式的求值使用堆栈结构很容易实现,且能很快求值。
注意:逆波兰记法并不是简单的波兰表达式的反转。因为对于不满足交换律的操作符,它的操作数写法仍然是常规顺序,如,波兰记法/ 6 3的逆波兰记法是6 3 /而不是3 6 /;数字的数位写法也是常规顺序。
4、表示法间转化
这里介绍一种简单的中缀表达式转化前后缀表达式的方法,比如这个式子:a+b*c-(d+e)
1.按照运算符的优先级对所有的运算单位加括号,式子变成:((a+(b*c))-(d+e))
2.前缀表达式,把运算符号移动到对应的括号前面,式子变成:-(+(a*(bc))+(de)),去掉括号:-+a*bc+de
3.后缀表达式,把运算符号移动到对应的括号后面,式子变成:((a(bc)*)+(de)+)-,去掉括号:abc*+de+-
下面的实例方法与上面的有所不同,因为情况更复杂了,请仔细推敲!
二、实例讲解
1、表达式转换
将以下中缀表达式:
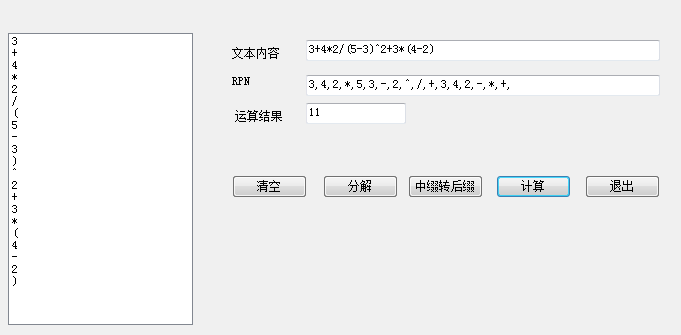
3+4*2/(5-3)^2+3*(4-2)
COS(900-3*10*30)+123.45+30*30-0.45+TAN(0)
转化为后缀表达式(RPN):
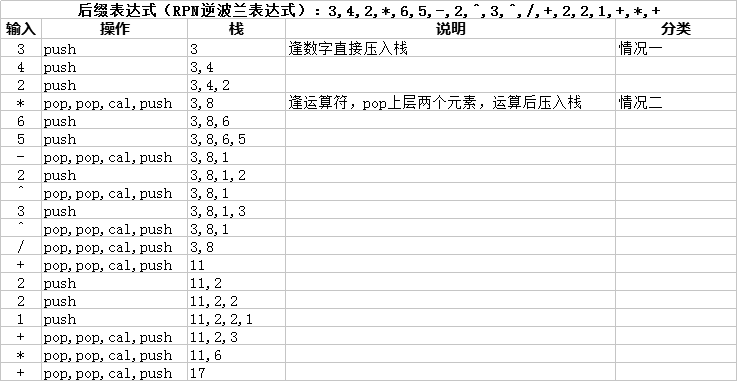
3,4,2,*,5,3,-,2,^,/,+,3,4,2,-,*,+
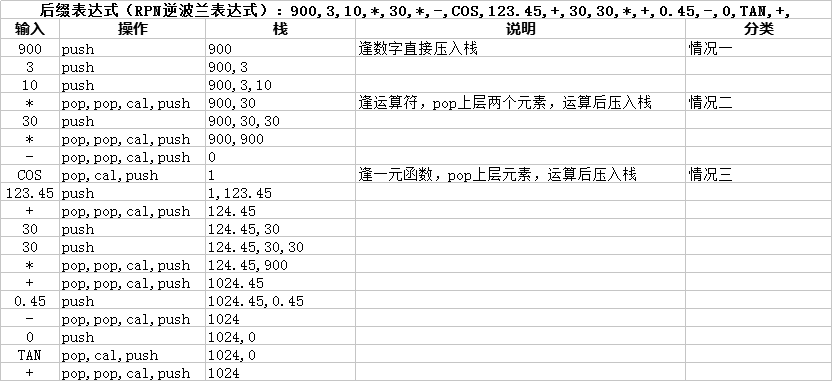
900,3,10,*,30,*,-,COS,123.45,+,30,30,*,+,0.45,-,0,TAN,+,
2、程序效果

3、编码分析
编码工作主要分为以下几块:
- 含有函数的中缀表达式转后缀表达式
- 区分数字、函数名、运算符;
- 将字符串拆分为数组形式,方便入栈;
- 判断运算符、函数的优先级,正确排列顺序;
- 针对后缀表达式进行计算
- 区分数字、函数名、运算符的不同操作;
- 根据运算规则不同进行入栈、出栈和计算;
4、转换流程
- 简单算术表达式的中缀转后缀

- 带有函数名的表达式,中缀转后缀

5、计算流程
- 简单算术后缀表达式计算
- 带有函数名的后缀表达式计算
6、实现代码
/*是否为纯数字。正则表达式实现*/
public static bool isNumber(string tmp)
{
return Regex.IsMatch(tmp, @"[0-9]+[.]{0,1}[0-9]*");
}
/*是否为需拆分的运算符+-*^/() */
public static bool isOp(string tmp)
{
bool bRet = false;
switch (tmp)
{
case "+":
case "-":
case "*":
case "/":
case "^":
case "(":
case ")":
bRet = true;
break;
default:
bRet = false;
break;
}
return bRet;
}
/*是否为一元函数名*/
public static bool isFunc(string tmp)
{
bool bRet = false;
switch (tmp)
{
case "SIN":
case "COS":
case "TAN":
case "SQRT":
bRet = true;
break;
default:
bRet = false;
break;
}
return bRet;
}
/*比较运算符及函数优先级。函数视作运算符进行操作。
返回值:1 表示 大于,-1 表示 小于,0 表示 相等 */
public static int compOper(string op1, string op2)
{
int iRet = 0;
Dictionary<string, int> dic = new Dictionary<string, int>();
dic.Add("+", 1);
dic.Add("-", 1);
dic.Add("*", 2);
dic.Add("/", 2);
dic.Add("^", 3);
dic.Add("SIN", 4);
dic.Add("COS", 4);
dic.Add("TAN", 4);
dic.Add("SQRT", 4);
dic.Add("(", 100);
dic.Add(")", 100);
if (dic[op1] > dic[op2])
iRet = 1;
else if (dic[op1] < dic[op2])
iRet = -1;
else
iRet = 0;
return iRet;
}
/*运算符、函数求值*/
public static double calValue(string op, string val1, string val2)
{
double dRet = 0.0d;
switch (op)
{
case "+":
dRet = double.Parse(val1) + double.Parse(val2);
break;
case "-":
dRet = double.Parse(val1) - double.Parse(val2);
break;
case "*":
dRet = double.Parse(val1) * double.Parse(val2);
break;
case "/":
if (double.Parse(val2) != 0)
dRet = double.Parse(val1) / double.Parse(val2);
else
MessageBox.Show("Error!");
break;
case "^":
dRet = Math.Pow(double.Parse(val1), double.Parse(val2));
break;
default:
break;
}
return dRet;
}
public static double calValue(string op, string val1)
{
double dRet = 0.0d;
switch (op)
{
case "SIN":
dRet = Math.Sin(double.Parse(val1));
break;
case "COS":
dRet = Math.Cos(double.Parse(val1));
break;
case "TAN":
dRet = Math.Tan(double.Parse(val1));
break;
case "SQRT":
if (double.Parse(val1) > 0)
dRet = Math.Sqrt(double.Parse(val1));
else
MessageBox.Show("Error!");
break;
default:
break;
}
return dRet;
}
/*按照=+-*^/()分隔出元素*/
public static string splitFunc(string tmp)
{
string sRet = tmp;
sRet = sRet.Replace("=", "\n=\n");
sRet = sRet.Replace("+", "\n+\n");
sRet = sRet.Replace("-", "\n-\n");
sRet = sRet.Replace("*", "\n*\n");
sRet = sRet.Replace("/", "\n/\n");
sRet = sRet.Replace("^", "\n^\n");
sRet = sRet.Replace("(", "\n(\n");
sRet = sRet.Replace(")", "\n)\n");
return sRet;
}
/*中缀表达式转后缀表达式。tmp为已经添加分隔符的中缀表达式字符串*/
public static string midToRPN(string tmp)
{
string sRet = ""; //返回值
string[] strArr = splitFunc(tmp.ToUpper()).Split('\n'); //字符串数组,存放分隔后的中缀表达式元素
Stack<string> strStk = new Stack<string>(); //栈,用于临时存放运算符和函数名
for (int i = 0; i < strArr.Length; i++)
{
if (string.IsNullOrEmpty(strArr[i])) //分隔后为空的元素剔除
continue;
else if (calString.isNumber(strArr[i])) //纯数字直接入队列
sRet += strArr[i] + ',';
else if (calString.isFunc(strArr[i])) //一元函数名直接入栈
strStk.Push(strArr[i]);
else if (calString.isOp(strArr[i])) //运算符特殊处理
{
if (strStk.Count != 0 && strStk.Peek() == "(" && strArr[i] != ")") //栈不为空,最上层为"(",则运算符直接入栈
{
strStk.Push(strArr[i]);
}
else if (strStk.Count != 0 && strArr[i] == ")") //栈不为空,遇")"则pop至"("为止
{
while (strStk.Peek() != "(")
sRet += strStk.Pop() + ',';
strStk.Pop();
if (strStk.Count != 0 && calString.isFunc(strStk.Peek())) //若"("后为一元函数名,则函数名也pop出
sRet += strStk.Pop() + ',';
}
else if (strStk.Count != 0 && calString.compOper(strArr[i], strStk.Peek()) == -1)
{ //栈不为空,运算符优先级小
while (strStk.Count != 0 && strStk.Peek() != "(" && calString.compOper(strArr[i], strStk.Peek()) == -1)
sRet += strStk.Pop() + ','; //则一直pop【存疑】
if (strStk.Count != 0) //pop至优先级不小于栈顶运算符则交换位置
sRet += strStk.Pop() + ','; //先pop
strStk.Push(strArr[i]); //再push
}
else if (strStk.Count != 0 && calString.compOper(strArr[i], strStk.Peek()) == 0)
{ //运算符优先级相同,先pop再push
sRet += strStk.Pop() + ',';
strStk.Push(strArr[i]);
}
else if (strStk.Count != 0 && calString.compOper(strArr[i], strStk.Peek()) == 1)
{ //运算符优先级大,直接入栈
strStk.Push(strArr[i]);
}
else //其他情况,入栈【存疑】
{
strStk.Push(strArr[i]);
}
}
}
while (strStk.Count > 0) //最后栈内元素全部pop出
{
sRet += strStk.Pop() + ',';
}
return sRet; //返回后缀表达式
}
/*根据传入的后缀表达式,求值。tmp为含逗号分隔符的后缀表达式 */
public static double calRPN(string tmp)
{
double dRet = 0.0d;
string[] strArr = tmp.Split(',');
Stack<string> strStk = new Stack<string>();
for (int i = 0; i < strArr.Length - 1; i++)
{
if (isNumber(strArr[i])) //纯数字入栈
strStk.Push(strArr[i]);
else if (isOp(strArr[i])) //二元运算符,pop两个元素,计算值后压入栈
strStk.Push(calValue(strStk.Pop(), strStk.Pop(), strArr[i]).ToString());
else if (isFunc(strArr[i])) //一元函数名,pop一个元素,计算后压入栈
strStk.Push(calValue(strArr[i], strStk.Pop()).ToString());
}
dRet = double.Parse(strStk.Pop()); //取最后栈中元素作为结果值
return dRet;
}
/*调用部分代码*/
private void btnTrans_Click(object sender, EventArgs e)
{
//中缀表达式转后缀表达式
this.tbRPN.Text = calString.midToRPN(this.tbOrigin.Text);
}
private void btnCal_Click(object sender, EventArgs e)
{
//后缀表达式求值
double tmp;
try
{
tmp = calString.calRPN(this.tbRPN.Text);
this.tbRes.Text = tmp.ToString();
}
catch (Exception ex)
{
MessageBox.Show(ex.ToString());
this.tbRes.Text = "Error";
}
finally
{
}
}


