递归程序的含义、实现机制以及复杂度计算

递归很美，美的让菜鸟找不着北。

阅读代码时我们总是根据函数的调用跳到不同的函数去阅读（除非函数名有很清晰明了），程序执行过程也是不断的跳转，一个函数里调用另一个函数很容易理解，但是函数里调用自己就有些令人迷惑了。

每次遇到递归的程序都有点发怵，主要问题有三个：一是递归程序含义的理解，二是递归实现的机制，三是递归程序复杂度的计算。

递归的定义

递归是直接或者间接调用自身的函数，当操作有某种重复模式的数据结构和问题时十分有效。

当要解决的问题可以转化为相似的子问题时，就是递归登场的时候了。

递归的例子

1、 1到n求和： s（n） = n + s（n-1）

2、 n的阶乘： f（n） = n * f（n-1）

3、 快速排序： quicksort（a，low，high） =>  quicksort（a，low，pivot-1） ⊙ quicksort（a，pivot+1， high）

4、 树的前序、中序、后续遍历： preorder（T） = >  read（T->data） preorder（T->leftChild） preorder（T->rightChild）

等等

递归的求解方式

可见，递归解决的问题总是有相同解决方法的子问题，从上述例子又可以发现递归也有不同的类型，例如1和2中，需要先计算出递归子问题的值，然后进行本步计算，而3快速排序中，需要先执行本步骤的分割，然后执行递归操作，本步骤不依赖与递归子问题的返回值。进一步考虑，可以将递归问题看作一棵树，例如快速排序，整个排序问题分割成左右两部分，每一部分又分割成两部分，类似于二叉树。递归问题的求解可以是由树根到叶子的自顶向下方式求解，如快排，也可以是由叶子节点到根节点的自底向上方式求解。再进一步，可以把递归问题的求解方式按照树的遍历方式分成三种，分别是前序遍历、中序遍历和后序遍历。

      阶乘                  f(4)                                                                排序               3 4 1 6 2 8               2 1 3 6 4 8

                             /     \                                                                                                                  /             \

                         4     *     f(3)                                                                                             2 1 => 1 2     3    6 4 8 => 4 6 8               

                                       /    \                                                                                                       \                    /      \

                                    3    *   f(2)                                                                                            1      2      3      4     6     8

                                               /   \

                                            2   *   f(1)                                                         结果 1 2 3 4 6 8

                                                     /    \

                                                  1   *   f(0)

                                                               \

                                                                   1

 

设计递归程序技巧和注意事项：

先假设后续调用步骤已经完成，那么本步骤该做什么，如果利用后续调用的结果（确定本步骤处理内容）；

考虑子问题如何形成，调用顺序是否影响运行结果（确定递归函数的调用时机和调用参数）；

考虑终止条件，用return返回或者用条件判断跳过递归调用（递归树达到叶子节点）。

读递归程序也可以参考这些技巧。

 

递归的实现机制

实际上递归函数的实现和普通函数的实现并没有多大差别，函数调用的时候发生的事情无非被调用函数参数压栈，原函数信息保存，被调用函数局部变量分配空间等，然后下一条执行的指令指向被调用函数。在递归函数中发生递归调用时，通用发生这些事情，区别就是下一条执行的指令指向了本函数的开始。这更像是一个Trick，但往往能有效的将程序员从大量的分析和思考中解放出来，将复杂的问题留给计算机去处理。

每次调用递归函数程序的栈都会增长，保持上一步的信息，处理子问题，当程序达到退出条件时开始返回，如果有返回值，上一步可以根据返回值完成该步骤的计算并返回值到再上一步，如果没有返回值则直接返回，直到完成各个递归最终跳出递归函数。根据阶乘递归画一遍函数调用的栈图就可以对递归深入理解。

参考Intel汇编语言程序设计第五版的递归式章节。

 

递归复杂度计算

递归式复杂度的计算是一个难点，面对一个递归表达式，很难很快判断出它的复杂度，这就需要一些处理过程。

主要的处理方法有三种：一是求解变形法、二是递归树法、三是主定理法。

1、求解变形法

将递归函数求解或者转化为容易判断复杂度的非递归形式，或者转换为容易求解的其他递归式。

例如 阶乘函数 f（n） = n * f（n-1）

其非递归的表达式即为 1*2*3......n，n次循环，每次循环做乘法，因此复杂度为O（n）。

又如递归方程 

 T（n） = 2 T（[√n]） + lgn  （其中[√n]表示根号n向下取整）

根式不容易计算，首先将其化为整数。设m = lgn ，则 T（2^m） = 2 T（2^m/2） + m

设S（m） = T （2^m）， 则 S（m） = 2S（m/2） + m

此递归式的复杂度容易计算，为O（mlgm） 

将其带回原表达式，可得 T（n） = T （2^m） = S（m） = O（mlgm） = O（lgnlglgn）。问题得解。

2、递归树法

上文已分析得递归方程的求解过程可以看作一颗树，将这颗树展开就得到了递归式的复杂度。

例： 递归式 T（n） = 3 T（n/4） + cn²

 

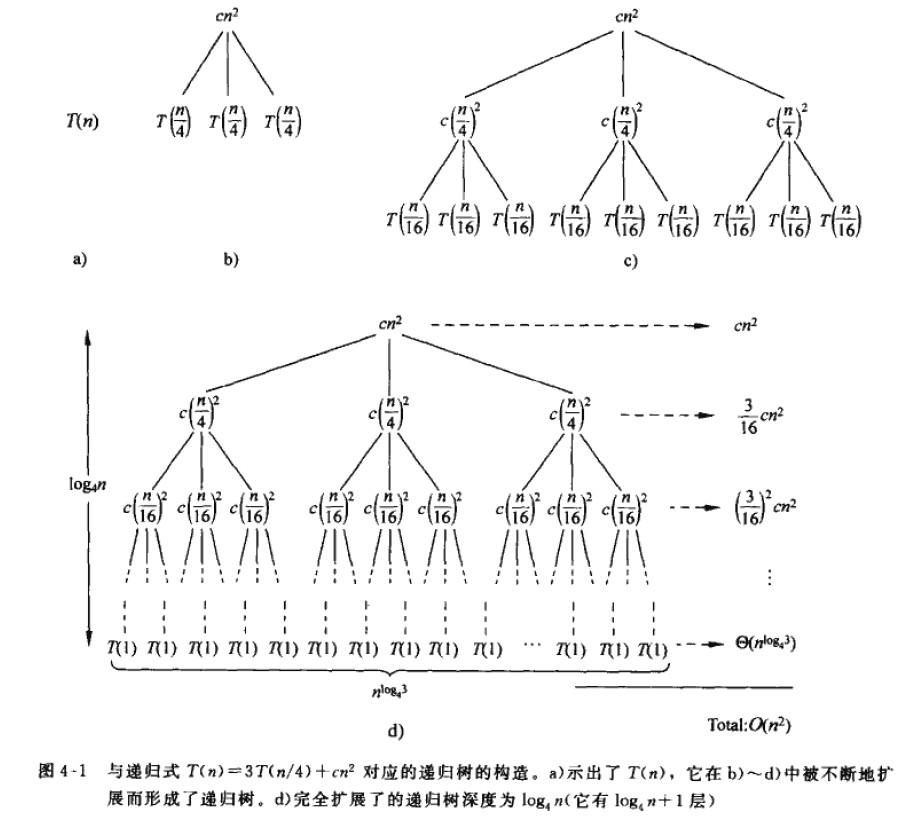
3、主定理

 主定理是解决递归问题的利器。但是主定理是有使用条件的，很多常见的问题可以转化为可以应用主定理的形式，这就省去了大量的分析，直接带入公式即可求解。

需要注意的是情况1中f（n）小于n^log_ba，而且是多项式的小，情况3中的大于也是同样，此条件一定要满足才可以应用主定理。情况2中是两者相当的情况，注意结果要乘以lgn。需要注意的是情况1和2以及2和3之间是有鸿沟的，例如f（n）小于n^log_ba但不是多项式的小，这就既不满足情况1也不满足情况2,这种情况就不能应用主定理。所以主定理并没有覆盖所有的递归式，只是多大部分遇到的递归式有效。

复杂度计算部分参考了算法导论递归式章节。