字符串算法专题之:字符串匹配算法
字符串匹配指的是从文本中找出给定字符串(称为模式)的一个或所有出现的位置。如C语言中的char *strstr(char *str1, char *str2);函数。字符串str1成为文本,str2称为模式。字符串匹配还分为精确匹配和近似匹配等。接下来就针对字符串匹配问题做详细分析。
1.最原始的字符串匹配算法(Brute Force)
Brute Force算法是最容易想到的,即将str2与str1的左对齐,然后依次比较各个字符,如果完全匹配,则返回开头位置,否则向右移动一个单位,重复此过程,直到不能完全匹配,返回空。这是一种滑动窗口的思想。
例如:在串S=”abcabcabdabba”中查找T=” abcabd”(我们可以假设从下标0开始):先是比较S[0]和T[0]是否相等,然后比较S[1] 和T[1]是否相等…我们发现一直比较到S[5]和T[5]才不等。如图:
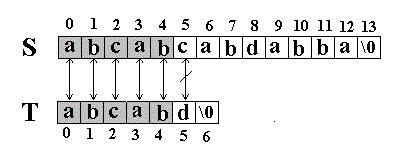
当这样一个失配发生时,T下标必须回溯到开始,S下标回溯的长度与T相同,然后S下标增1,然后再次比较。如图:

这次立刻发生了失配,T下标又回溯到开始,S下标增1,然后再次比较。如图:
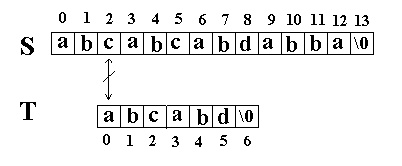
又一次发生了失配,所以T下标又回溯到开始,S下标增1,然后再次比较。这次T中的所有字符都和S中相应的字符匹配了。函数返回T在S中的起始下标3。如图:

此方法最容易想到,直截了当,没有做任何优化,匹配的时间复杂度为O(mn),其中m为文本串的长度,n为模式串的长度。比较过程还可以用memcmp来进行加点速度,但是总体复杂度不变。
参考strstr函数的代码:
char *strstr( const char *s1, const char *s2 )
{
int len2;
if ( !(len2 = strlen(s2)) )
return (char *)s1;
for ( ; *s1; ++s1 )
{
if ( *s1 == *s2 && strncmp( s1, s2, len2 )==0 )
return (char *)s1;
}
return NULL;
}
2. 记住做过的比较-记住前缀(KMP算法)
原始的算法之所以慢,是因为它太健忘了,每次做完比较不进行记录,这样导致很多比较是重复的。
原始算法中,每次发现不匹配则将模式串向右移动一个单位。而在KMP算法中,根据模式串的结构,每次发生不匹配可能向右移动多个单位,这样就减少了很多无用的比较,但是这样的结果还准确吗,KMP算法的规则和几个定理可以保证KMP算法的正确性。
还是相同的例子,在S=”abcabcabdabba”中查找T=”abcabd”,如果使用KMP匹配算法,当第一次搜索到S[5] 和T[5]不等后,S下标不是回溯到1,T下标也不是回溯到开始,而是根据T中T[5]==’d’的模式函数值(next[5]=2,为什么?后面讲),直接比较S[5] 和T[2]是否相等,因为相等,S和T的下标同时增加;因为又相等,S和T的下标又同时增加。。。最终在S中找到了T。如图:
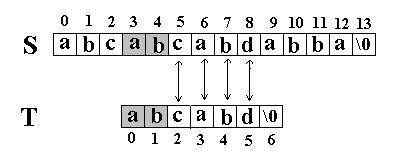
对于一般文稿中串的匹配,简单匹配算法的时间复杂度可降为O (m+n),因此在多数的实际应用场合下被应用。
KMP算法的核心思想是利用已经得到的部分匹配信息来进行后面的匹配过程。看前面的例子。为什么T[5]==’d’的模式函数值等于2(next[5]=2),其实这个2表示T[5]==’d’的前面有2个字符和开始的两个字符相同,且T[5]==’d’不等于开始的两个字符之后的第三个字符(T[2]=’c’).如图:

在KMP算法中,为了确定在匹配不成功时,下次匹配时j的位置,引入了next[]数组,next[j]的值表示P[0...j-1]中最长后缀的长度等于相同字符序列的前缀。
KMP算法的具体规则如下:
首先计算串的模式值:
(1)next[0]= -1 意义:任何串的第一个字符的模式值规定为-1。
(2)next[j]= -1 意义:模式串T中下标为j的字符,如果与首字符相同,且j的前面的1—k个字符与开头的1—k个字符不等(或者相等但T[k]==T[j])(1≤k<j)。如:T=”abCabCad” 则 next[6]=-1,因T[3]=T[6]
(3)next[j]=k 意义:模式串T中下标为j的字符,如果j的前面k个字符与开头的k个字符相等,且T[j] != T[k] (1≤k<j)。 即T[0]T[1]T[2]。。。T[k-1]==T[j-k]T[j-k+1]T[j-k+2]…T[j-1]且T[j] != T[k].(1≤k<j);
(4) next[j]=0 意义:其他情况。
在匹配过程称,若发生不匹配的情况,如果next[j]>=0,则目标串的指针i不变,将模式串的指针j移动到next[j]的位置继续进行匹配;若next[j]=-1,则将i右移1位,并将j置0,继续进行比较。
仔细思考这些规则,就会发现KMP算法的精妙之处,此处我谈一部分。
首先为什么T[j] != T[k]时next[j]=k,而T[j] == T[k]时next[j] = -1?因为模式串T下标j位置前面k个字符已经与文本串S下标i位置前k个字符匹配,此时这个子串又和T开头的k个字符的子串匹配,如果T[j] == T[k],那S[i]肯定与T[k]不匹配,不用再比较可以直接向右移位,如果T[j] != T[k],则S[i]和T[k]进行比较。
跳过的子串不可能匹配吗?分析可得,如果j的前面k个字符与开头的k个字符相等,且T[j] != T[k] 。至少移动至此位置才能使子串再次匹配,否则不可能完全匹配。
3. 记住做过的比较-记住后缀(Boyer-Moore算法)
Boyer-Moore算法也是对做过的比较做记录,然后每次尝试移动最大的安全距离,理论上时间复杂度和KMP 差不多,但是实际上却比KMP 快3-5倍。
BM算法在移动模式串的时候是从左到右,而进行比较的时候是从右到左的。
BM算法实际上包含两个并行的算法,坏字符算法和好后缀算法。这两种算法的目的就是让模式串每次向右移动尽可能大的距离(j+=x,x尽可能的大)
例主串和模式串如下:
主串 : mahtavaatalomaisema omalomailuun
模式串: maisemaomaloma
好后缀:模式串中的aloma为“好后缀”。
坏字符:主串中的“t”为坏字符。
好后缀算法有两种情况:
Case1:模式串中有子串和好后缀安全匹配,则将最靠右的那个子串移动到好后缀的位置。继续进行匹配。
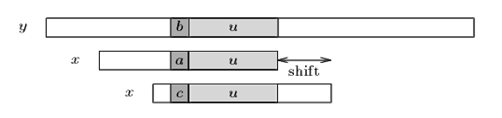
Case2:如果不存在和好后缀完全匹配的子串,则在好后缀中找到具有如下特征的最长子串,使得P[m-s…m]=P[0…s]。如图:
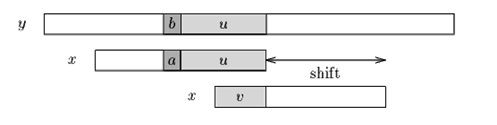
当出现一个坏字符时, BM算法向右移动模式串, 让模式串中最靠右的对应字符与坏字符相对,然后继续匹配。坏字符算法也有两种情况。
Case1:模式串中有对应的坏字符时,见图。

Case2:模式串中不存在坏字符。见图。

BM算法是每次向右移动模式串的距离是,按照好后缀算法和坏字符算法计算得到的最大值。
shift(好后缀)和shift(坏字符)通过模式串的预处理数组的简单计算得到。好后缀算法的预处理数组是bmGs[],坏字符算法的预处理数组是BmBc[]。
4. Sunday算法
Sunday算法其实思想跟BM算法很相似,只不过Sunday算法是从前往后匹配,在匹配失败时关注的是文本串中参加匹配的最末位字符的下一位字符。如果该字符没有在匹配串中出现则直接跳过,即移动步长= 匹配串长度+ 1;否则,同BM算法一样其移动步长=匹配串中最右端的该字符到末尾的距离+1。
5. 其他字符串匹配算法
字符串匹配算法还有其他一些,如Horspool, Rabin-Karp等。
总结
经过这次整理发现看似字符串算法中最简单的字符串匹配都有这么多的算法,而且很多算法理解起来还需要花费一些时间。博客中提到的4个算法运行效率是递增顺序,可以看到不同算法的主要区别是发现失配是如果移动最大安全距离进行下一次匹配。BF算法是简单的完全遍历,KMP算法根据模式串特征进行移动,BM算法根据好后缀和坏字符进行移动,Sunday算法根据字符串末位字符的下一位字符进行移动。都是抓住匹配过程中字符串的某个特点,快速排除不可能匹配的情况,进行最有可能的匹配。
到目前为止算法中的某些细节还不是特别清楚,有新收获的时候再更新此文。
参考:
KMP算法
http://www.cppblog.com/oosky/archive/2006/07/06/9486.html
http://www.cnblogs.com/dolphin0520/archive/2011/08/24/2151846.html
BM算法
http://blog.csdn.net/sealyao/article/details/4568167





