20182301 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结
教材学习内容总结
图的结构构成
-
顶点(vertex):图中的数据元素,如图一
-
边(edge):图中连接这些顶点的线,如图一
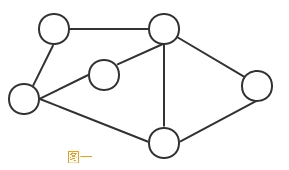
-
G=(V,E) 或者 G=(V(G),E(G))
- 其中 V(G)表示图结构所有顶点的集合,顶点可以用不同的数字或者字母来表示。E(G)是图结构中所有边的集合,每条边由所连接的两个顶点来表示。
- 图结构中顶点集合V(G)不能为空,必须包含一个顶点,而图结构边集合可以为空,表示没有边。
图的基本概念
-
无向图
-
如果一个图结构中,所有的边都没有方向性,那么这种图便称为无向图。典型的无向图,如图二所示。由于无向图中的边没有方向性,这样我们在表示边的时候对两个顶点的顺序没有要求。例如顶点VI和顶点V5之间的边,可以表示为(V2, V6),也可以表示为(V6,V2)。

-
有向图
-
一个图结构中,边是有方向性的,那么这种图就称为有向图,如图三所示。由于图的边有方向性,我们在表示边的时候对两个顶点的顺序就有要求。我们采用尖括号表示有向边,例如<V2,V6>表示从顶点V2到顶点V6,而<V6,V2>表示顶点V6到顶点V2。
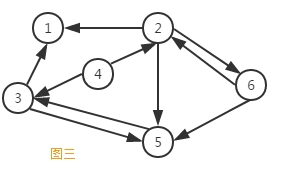
-
顶点的度
-
连接顶点的边的数量称为该顶点的度。顶点的度在有向图和无向图中具有不同的表示。对于无向图,一个顶点V的度比较简单,其是连接该顶点的边的数量,记为D(V)。
-
对于有向图要稍复杂些,根据连接顶点V的边的方向性,一个顶点的度有入度和出度之分。
- 入度是以该顶点为端点的入边数量, 记为ID(V)。
- 出度是以该顶点为端点的出边数量, 记为OD(V)。
-
邻接矩阵
-
邻接顶点是指图结构中一条边的两个顶点。邻接顶点在有向图和无向图中具有不同的表示。对于无向图,邻接顶点比较简单。
-
对于有向图要稍复杂些,根据连接顶点V的边的方向性,两个顶点分别称为起始顶点(起点或始点)和结束顶点(终点)。有向图的邻接顶点分为两类:
- 入边邻接顶点:连接该顶点的边中的起始顶点。例如,对于组成<V2,V6>这条边的两个顶点,V2是V6的入边邻接顶点。
- 出边邻接顶点:连接该顶点的边中的结束顶点。例如,对于组成<V2,V6>这条边的两个顶点,V6是V2的出边邻接顶点。
-
无向完全图
-
如果在一个无向图中, 每两个顶点之间都存在条边,那么这种图结构称为无向完全图。典型的无向完全图,如图四所示。
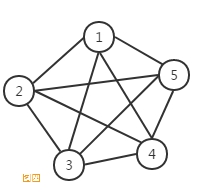
-
理论上可以证明,对于一个包含M个顶点的无向完全图,其总边数为M(M-1)/2。比如图四总边数就是5(5-1)/ 2 = 10。
-
有向完全图
-
如果在一个有向图中,每两个顶点之间都存在方向相反的两条边,那么这种图结构称为有向完全图。典型的有向完全图,如图五所示。
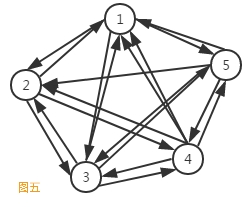
-
理论上可以证明,对于一个包含N的顶点的有向完全图,其总的边数为N(N-1)。这是无向完全图的两倍,这个也很好理解,因为每两个顶点之间需要两条边。
-
有向无环图(DAG图)
-
如果一个有向图无法从某个顶点出发经过若干条边回到该点,则这个图是一个有向无环图。
-
有向无环图可以利用在区块链技术中。
-
无权图和有权图
-
这里的权可以理解成一个数值,就是说节点与节点之间这个边是否有一个数值与它对应,对于无权图来说这个边不需要具体的值。对于有权图节点与节点之间的关系可能需要某个值来表示,比如这个数值能代表两个顶点间的距离,或者从一个顶点到另一个顶点的时间,所以这时候这个边的值就是代表着两个节点之间的关系,这种图被称为有权图;
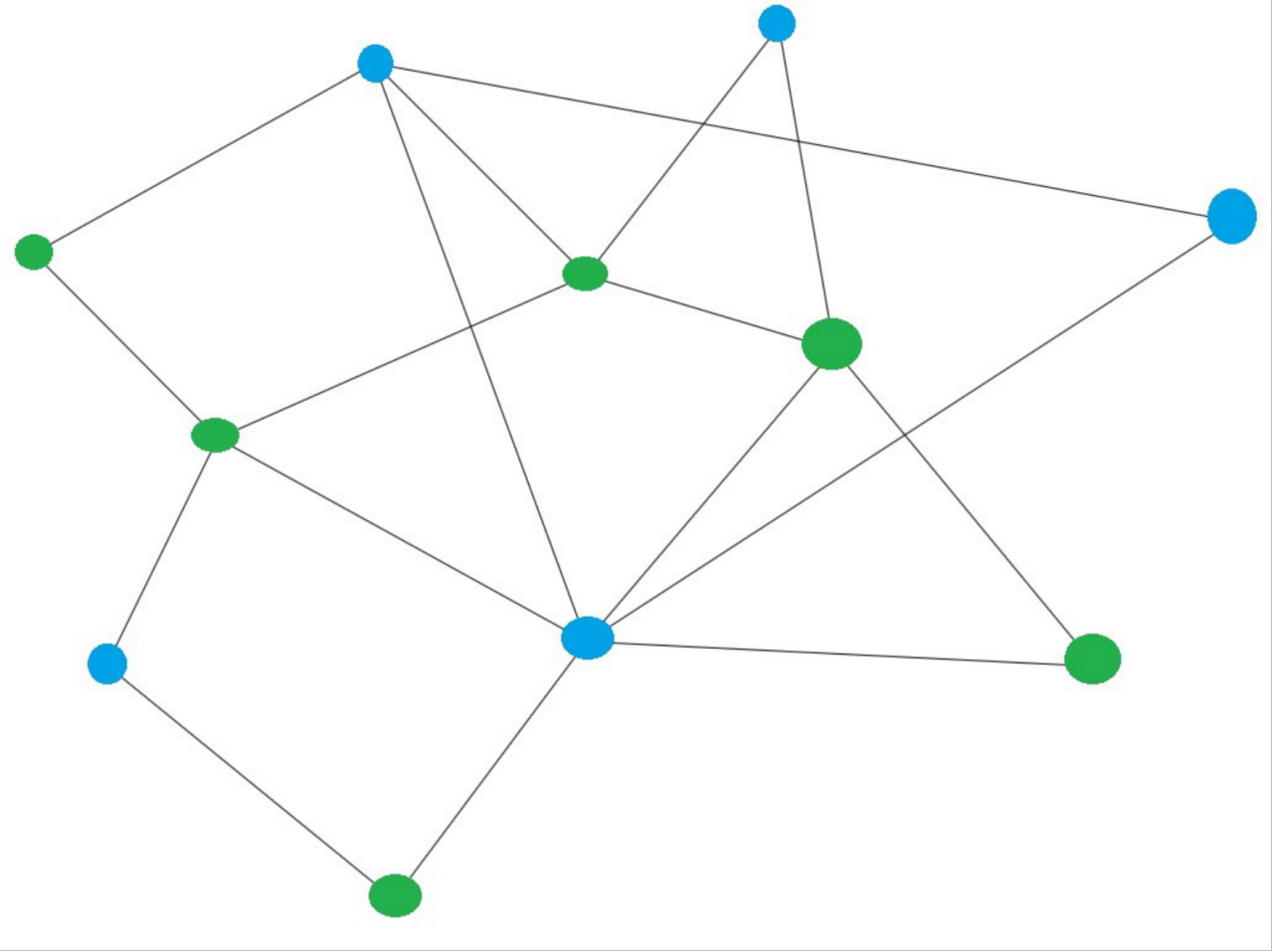
-
图的连通性
-
图的每个节点不一定每个节点都会被边连接起来,所以这就涉及到图的连通性,如下图:

-
可以发现上面这个图不是完全连通的。
-
简单图 ( Simple Graph)
-
对于节点与节点之间存在两种边,这两种边相对比较特殊
- 自环边(self-loop):节点自身的边,自己指向自己。
- 平行边(parallel-edges):两个节点之间存在多个边相连接。
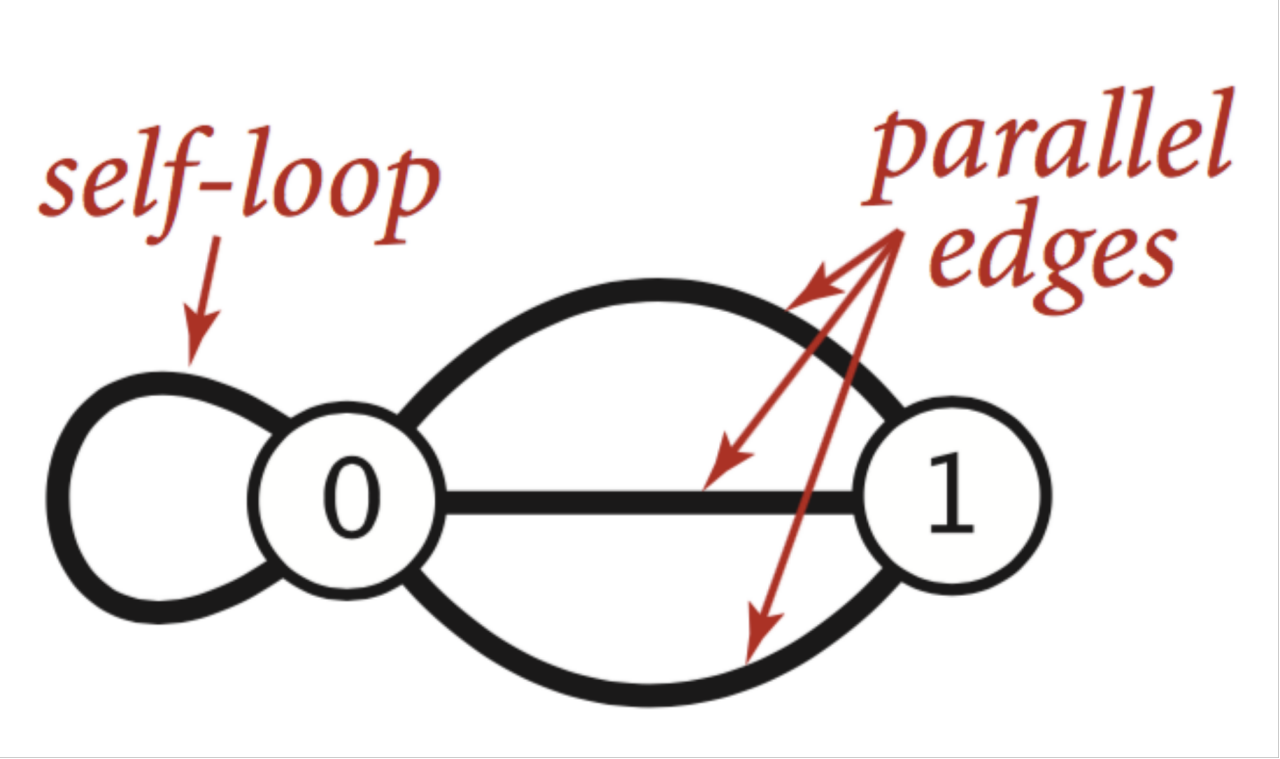
-
这两种边都是有意义的,比如从A城市到B城市可能不仅仅有一条路,比如有三条路,这样平行边就可以用到这种情况。不过这两种边在算法设计上会加大实现的难度。而简单图就是不考虑这两种边。
常见图的算法
-
广度优先遍历
- 遍历方法:从一个顶点开始,辐射状地优先遍历其周围较广的区域
- 实现方法:需要一个队列来保存遍历过的定点顺序,以便按出队的顺序再去访问这些顶点的邻接顶点
- 顶部伪代码:
- 访问初始结点v并标记结点v为已访问。
- 结点v入队列
- 当队列非空时,继续执行,否则算法结束。
- 出队列,取得队头结点u。
- 查找结点u的第一个邻接结点w。
- 若结点u的邻接结点w不存在,则转到步骤3;否则循环执行以下三个步骤:
- 若结点w尚未被访问,则访问结点w并标记为已访问。
- 结点w入队列
- 查找结点u的继w邻接结点后的下一个邻接结点w,转到步骤6。
- 图片解释:其广度优先算法的遍历顺序为:1->2->3->4->5->6->7->8
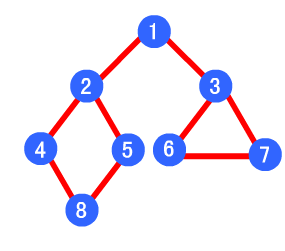
-
深度优先遍历
- 遍历方法:从一个顶点开始,沿边去探寻每一个顶点。(通俗一点:一条道走到黑!)
- 实现方法:通过栈来保存遍历过的定点顺序,遇到一个顶点,只是先获得它,并不出栈(因为要多次利用它),然后把它的第一个未被访问的节点入队列。如果没有相邻的未被访问的顶点,才把这个顶点出栈。
- 顶部伪代码:
- 访问初始结点v,并标记结点v为已访问。
- 查找结点v的第一个邻接结点w。
- 若w存在,则继续执行4,否则算法结束。
- 若w未被访问,对w进行深度优先遍历递归(即把w当做另一个v,然后进行步骤123)。
- 查找结点v的w邻接结点的下一个邻接结点,转到步骤3。
- 图片解释:其深度优先遍历顺序为1->2->4->8->5->3->6->7
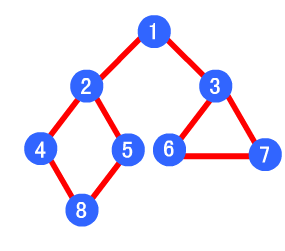
最小生成树
- 在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。
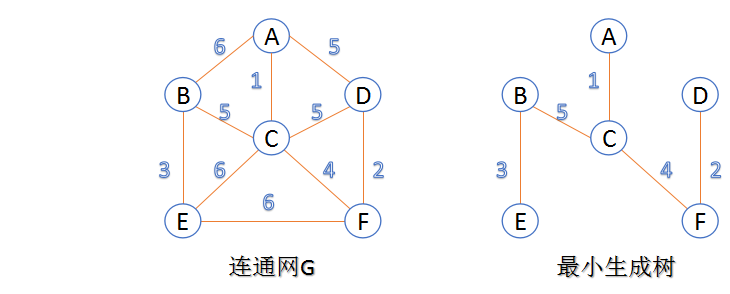
- Kruskal算法
- 此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
- 把图中的所有边按代价从小到大排序;
- 把图中的n个顶点看成独立的n棵树组成的森林;
- 按权值从小到大选择边,所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
- 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
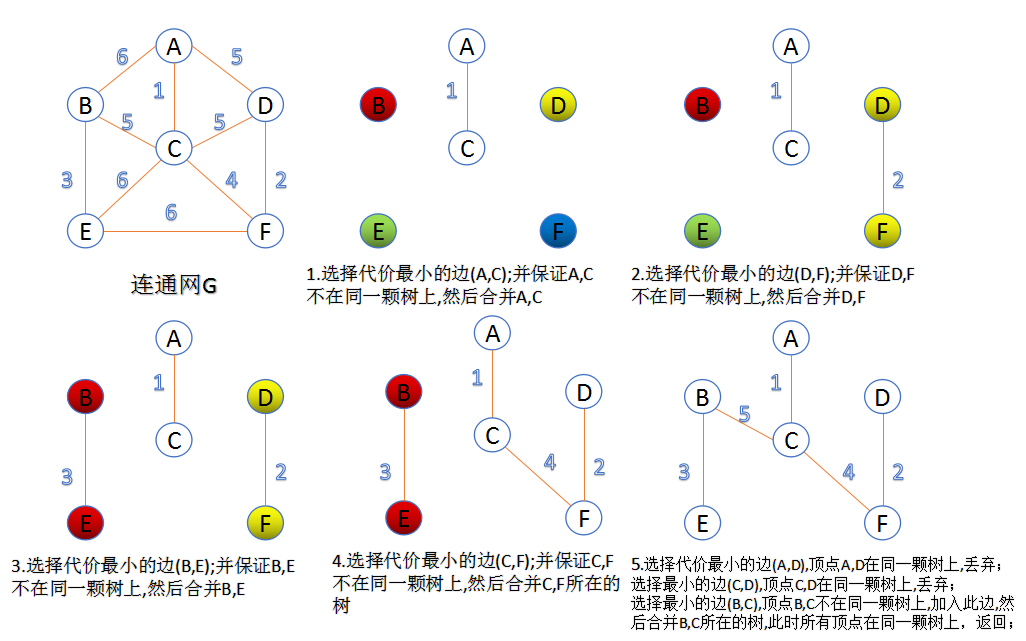
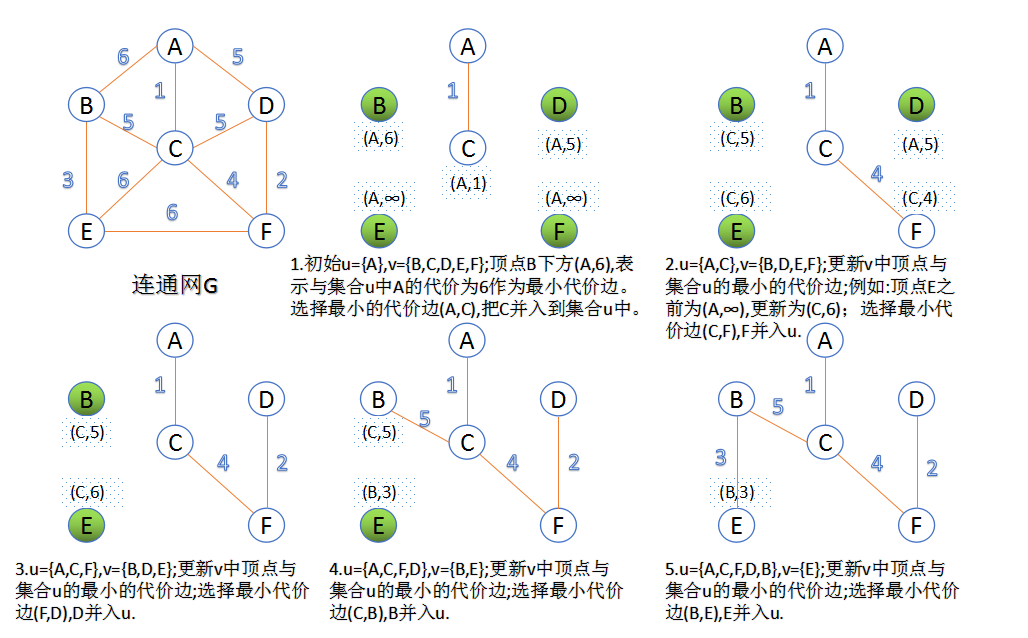
- Prim算法
- 此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
- 图的所有顶点集合为VV;初始令集合u={s},v=V−uu={s},v=V−u;
- 在两个集合u,vu,v能够组成的边中,选择一条代价最小的边(u0,v0)(u0,v0),加入到最小生成树中,并把v0v0并入到集合u中。
- 重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。
最短路径问题
-
无权图的单源最短路径
-
首先,我们将起点的路径长设为0,其他顶点路径长设为负数(也可以是其他不可能的值,图例中用?表示),下例以v1作为起点
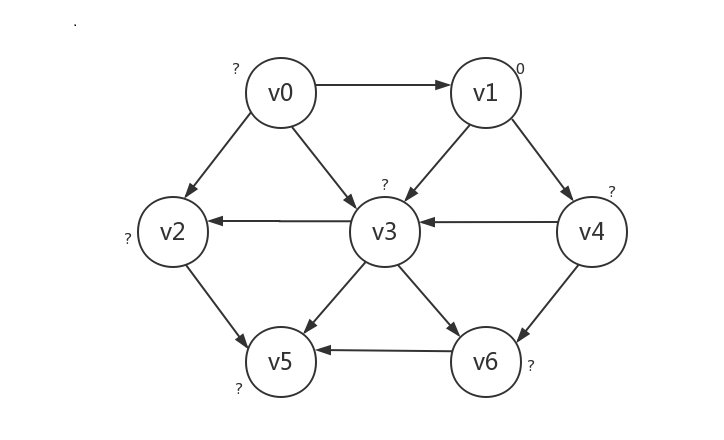
-
接着我们将起点所指向的顶点的路径长设为1,可以肯定的是,只有被路径长为0的起点所指向的顶点的路径长为1,本例中即v3和v4:
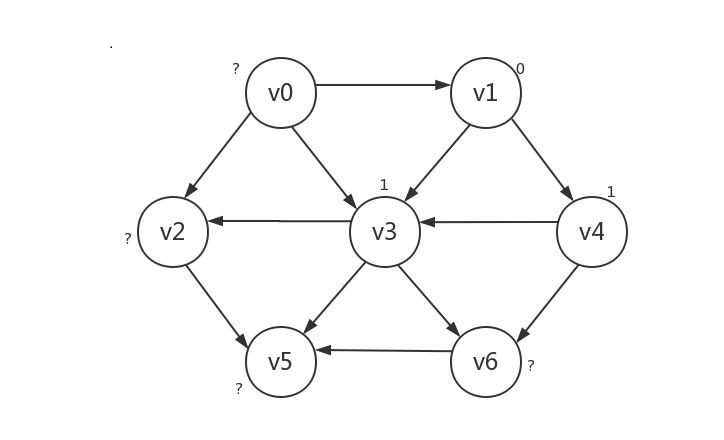
-
接下来,我们将路径长为1的顶点(v3和v4)所指向的顶点的路径长设为2,同样可以肯定,只有被路径长为1的顶点所指向的顶点的路径长为2。不过此时会遇到一个问题:v3是v4所指向的顶点,但v3的路径长显然不应该被设为2。所以我们需要对已知路径长的顶点设一个“已知”标记,已知的顶点不再更改其路径长,具体做法在给出代码时将写明。本例中,路径长要被设为2的顶点是v2、v5、v6
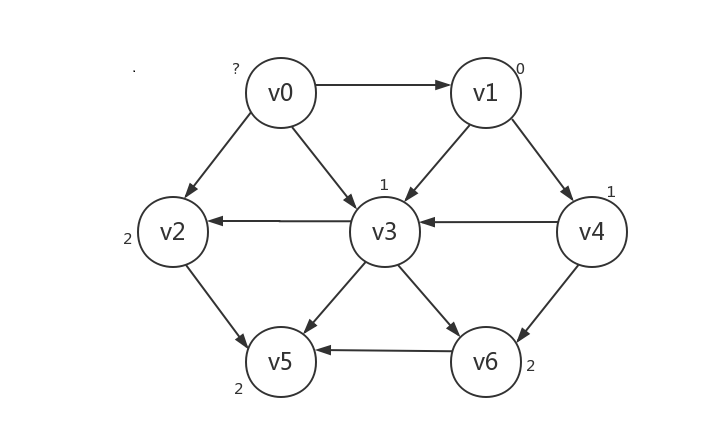
-
规律是:将路径长为i的顶点所指向的未知顶点的路径长设为i+1,i从0开始,结束条件即:当前路径长为i的顶点没有指向其它顶点,或所指向的顶点均为已知。
-
需要注意的是结束条件的说法,我们并没有要求所有顶点都变为已知,因为确定某顶点为起点后,是有可能存在某个顶点无法由起点出发然后到达的,比如我们的例子中的v0,不存在从v1到v0的路径。
-
将最短路径的计算结果存于一个线性表中,其结构如下:

-
其中“一行”为线性表中的一个元素,每一行的四个单元格就是一个元素中的四个域:顶点、是否已知、与起点最短路径长、最短路径中自身的前一个顶点。
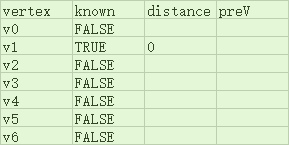
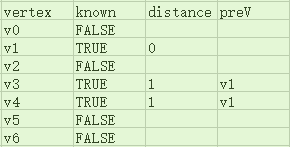
-
那么之前计算最短路径的过程用这个表来表示的话,就是下面这样:

-
简单伪代码
//无权最短路径计算,图存于邻接表graph,结果存入pathTable,起点即start
void unweightedPath(Node* graph,struct pathNode* pathTable,size_t start)
{
pathTable[start].known=true;
pathTable[start].distance=0; //若pathTable[x].distance为0,则其preV是无用的,我们不予理睬
//初始化pathTable中的其他元素
//curDis即当前距离,我们要做的是令distance==curDis的顶点所指的未知顶点的distance=curDis+1
for(int curDis=0;curDis<numVertex;++curDis)
{
for(int i=0;i<numVertex;++i)
{
if(!pathTable[i].known&&pathTable[i].distance==curDis)
{
pathTable[i].known=true;
//遍历pathTable[i]所指向的顶点X
{
if(!pathTable[X].known)
{
pathTable[X].preV=i;
pathTable[X].distance=curDis+1;
}
}
}
}
}
}
-
令已知顶点所指未知顶点的distance=curDis+weight
-
解决的思路是:我们罗列出所有已知顶点指向的所有未知顶点,看这些未知顶点中谁的distance被修改后会是最小的,最小的那个我们就修改其distance,并认为它已知。
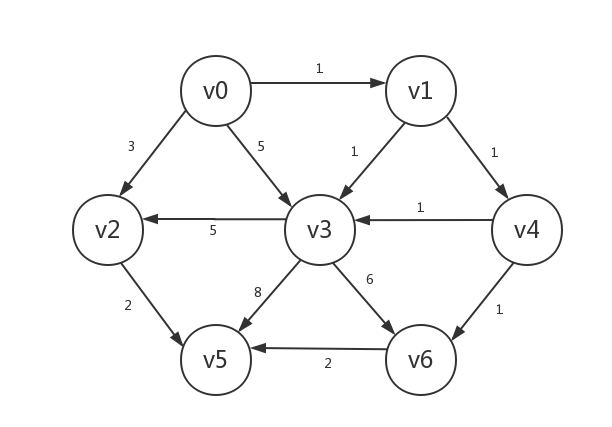
-
首先是正常的初始化(我们将边的权重也标识出来),假设起点为v0:
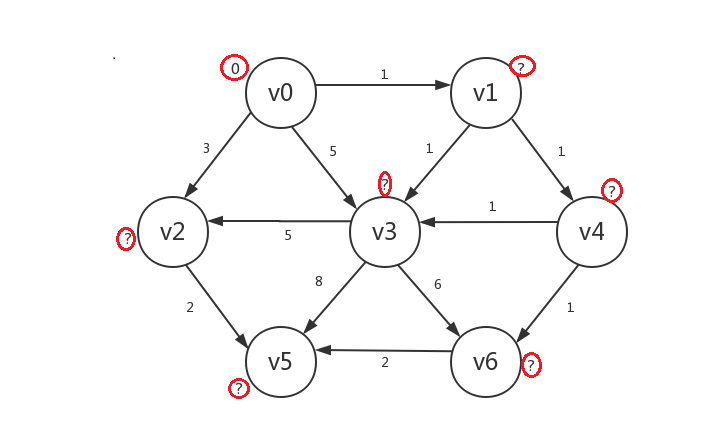
-
接着我们罗列出所有已知顶点(只有v0)指向的所有未知顶点:v1、v2、v3。然后发现若修改它们的distance,则v1.distance=v0.distance+1=1,v2.distance=v0.distance+3=3,v3.distance=v0.distance+5=5。显然v1被修改后的distance是未知顶点中最小的,所以我们只修改v1的distance,并将v1设为已知,v2、v3不动:
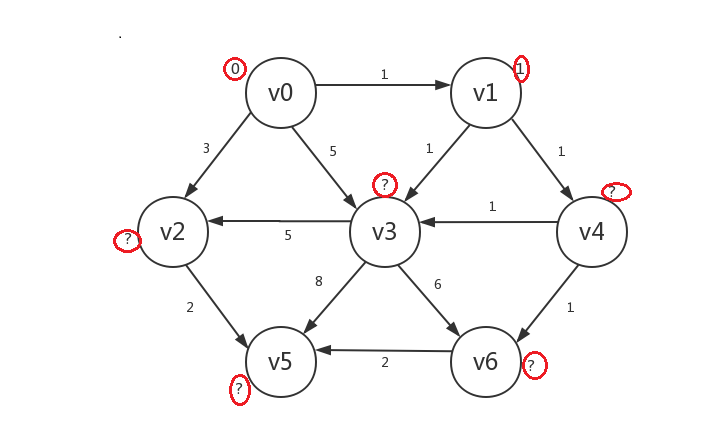
-
接着我们继续罗列出所有已知顶点(v0、v1)指向的所有未知顶点:v2、v3、v4。然后发现若修改它们的distance,则v2.distance=v0.distance+3=3,v4.distance=v1.distance+1=2,v3.distance=v1.distance+1=2(虽然v0也指向v3,但是通过v0到v3的路径长大于从v1到v3,所以v3的distance取其小者),其中v3和v4的新distance并列最小,我们任选其一比如v4,然后只修改v4的distance,并将v4设为已知,其它不动:

-
继续,我们罗列出所有已知顶点(v0、v1、v4)指向的所有未知顶点:v2、v3、v6,发现若修改,则v2.distance=3,v3.distance=2,v6.distance=3,所以我们只修改v3的distance,并将v3设为已知:
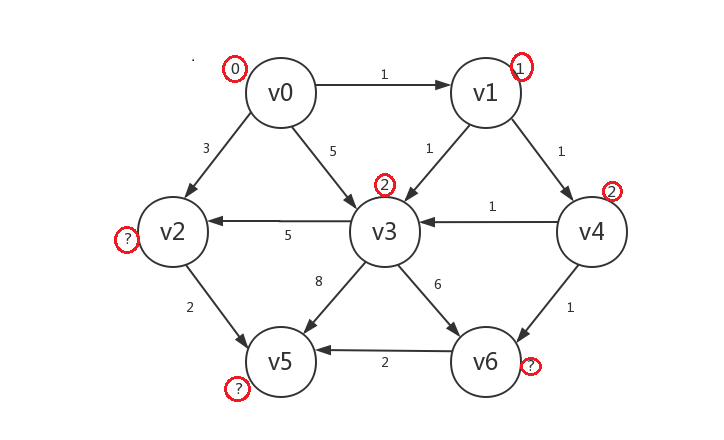
-
继续,我们罗列出所有已知顶点(v0、v1、v3、v4)指向的所有未知顶点:v2、v5、v6,发现若修改,则v2.distance=3,v5.distance=10,v6.distance=3,我们在v2和v6中任选一个如v2,只修改v2.distance,并将v2设为已知:
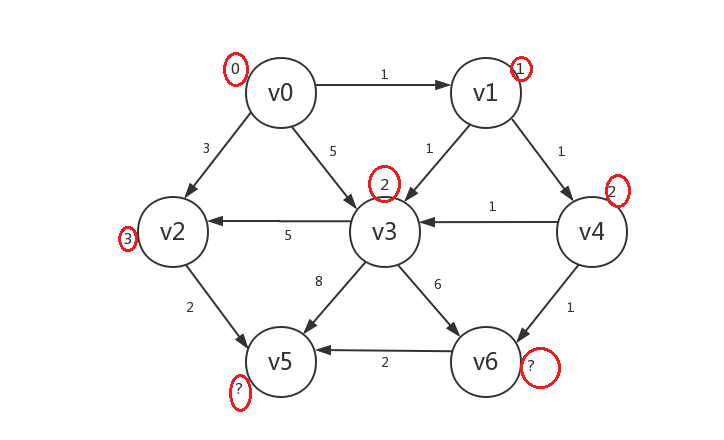
-
继续,我们罗列出所有已知顶点指向的所有未知顶点:v5、v6,发现若修改,则v5.distance=5,v6.distance=3,所以我们只修改v6:
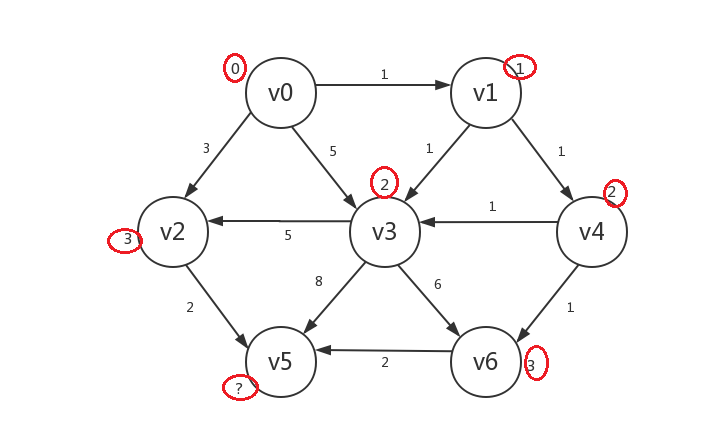
-
最后,罗列出的未知顶点只有v5,若修改,其distance=5,我们将其修改并设为已知,算法结束:
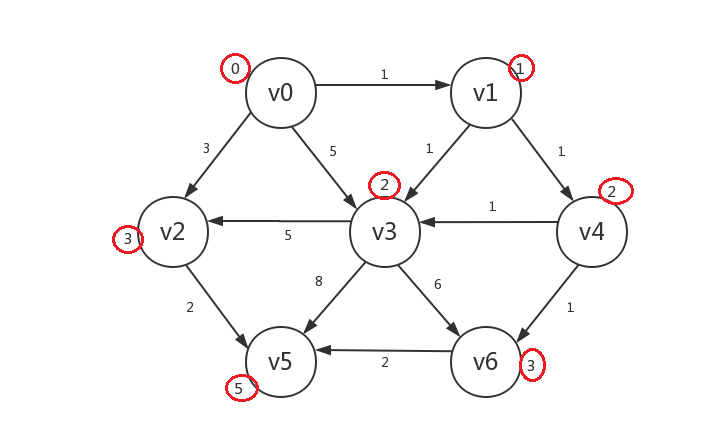
-
有权图伪代码:
//有权最短路径计算,图存于邻接表graph,结果存入pathTable,起点即start
void weightedPath(Node* graph,struct pathNode* pathTable,size_t start)
{
//初始化pathNode数组
size_t curV;
while(true)
{
//找到可确定distance的未知顶点中新distance最小的那个,存入curV,若没有则跳出循环
//令pathNode[curV].distance和pathNode[curV].prev修改为正确的值
pathNode[curV].known=true;
}
}
教材学习中的问题和解决过程
-
问题1:了解拓扑排序
-
问题1解决方案:(详见链接5)

-
拓扑排序就是对图中顶点进行的排序,其要求是:若存在从vx到vy的路径,那么排序结果中vx必须在vy之前。
-
进行拓扑排序的图必须是有向无圈图。
- 在无向图中,若存在边(vx,vy)则必存在边(vy,vx),那么依拓扑排序的要求,vx就必须在vy的前面,同时vy又必须在vx前面,这显然是矛盾的,所以拓扑排序只能用于有向图。
- 在有向有圈图中,比如上图,其中的圈v0-v1-v4-v3-v0就暗含着两条子路径:v0-v1-v4和v4-v3-v0,依前一条路径而言,排序结果中v0必须在v4前面,而依后一条路径而言,v4又必须在v0前面,这显然也是矛盾的,所以拓扑排序只能用于有向无圈图。
-
有向无圈图的两个特点:
- 若图有向无圈,则必然存在一个入度为0的顶点。
- 若图有向无圈,则去掉其入度为0的顶点及相连边(必为以该顶点为起点的有向边)后,图依然是有向无圈图。
-
伪代码:
void topSort(graph* g,size_t numVertex,size_t topResult)
{
//两个表示顶点的变量,后面用
size_t tempV,adjV;
//存储各顶点入度的数组,顶点x的入度为indegree[x]
size_t indegree[numVertex];
伪:根据图g初始化indegree数组
for(int i=0;i<numVertex;++i)
{
伪:从indegree中找到一个入度为0的顶点,存入tempV
if(伪:没找到入度为0的顶点)
伪:报错、返回
topResult[i]=tempV;
伪:通过g[tempV]遍历tempV为起点的边的终点,存入adjV
indegree[adjV]--;
}
}
- 问题2:图的广度优先遍历和深度优先遍历最根本的区别是什么?
- 问题2解决方案:
- 深度优先遍历的非递归做法时采用栈;广度优先遍历的非递归做法时采用队列
- 深度优先遍历是把每个分支深入到不能深入为止。具体的有先序遍历、中序遍历、后序遍历;广度优先遍历又称层序遍历,从上往下一层一层遍历
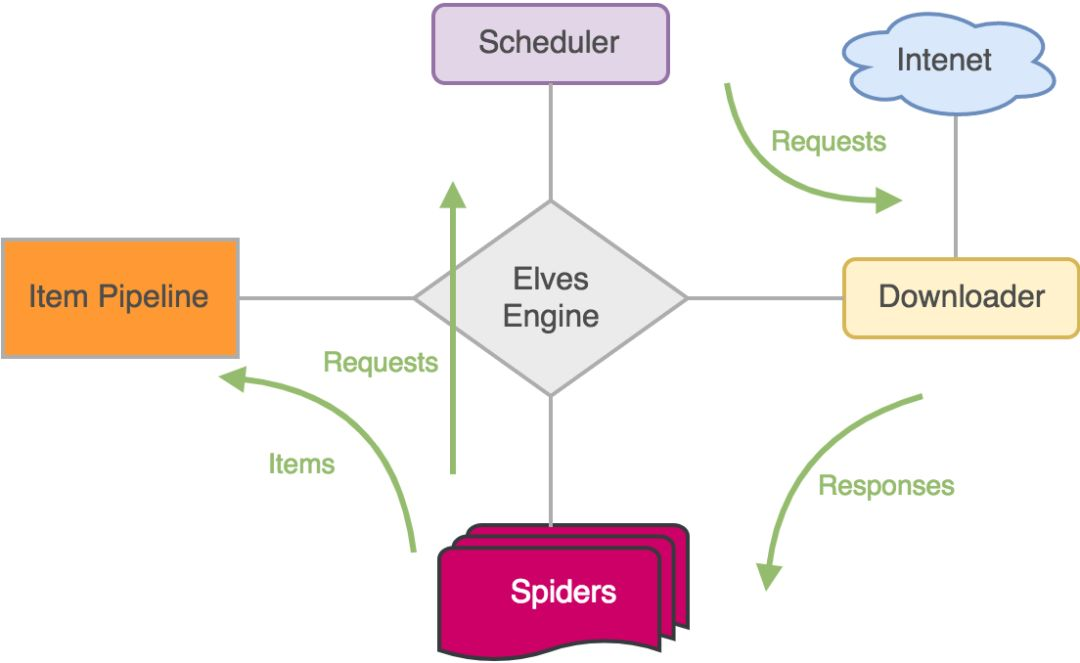
- 问题3:关于深度优先遍历的网络爬虫,深入了解一下
- 问题3解决方案:
- 网络爬虫(又被称为网页蜘蛛,网络机器人,在FOAF社区中间,更经常的称为网页追逐者),是一种按照一定的规则,自动地抓取万维网信息的程序或者脚本。另外一些不常使用的名字还有蚂蚁、自动索引、模拟程序或者蠕虫。
- 访问频率限制;
- Header头部信息校验;
- 采用动态页面生成;
- 采用动态页面生成;
- 登录限制;
- 验证码限制等。
- 爬虫实例
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStream;
import java.io.InputStreamReader;
import java.net.MalformedURLException;
import java.net.URL;
import org.jsoup.Jsoup;
import org.jsoup.nodes.Document;
import org.jsoup.nodes.Element;
import org.jsoup.select.Elements;
public class Reptile {
public static void main(String[] args) {
// 传入你所要爬取的页面地址
String url1 = "http://www.xxxx.com.cn/";
// 创建输入流用于读取流
InputStream is = null;
// 包装流, 加快读取速度
BufferedReader br = null;
// 用来保存读取页面的数据.
StringBuffer html = new StringBuffer();
// 创建临时字符串用于保存每一次读的一行数据,然后 html 调用 append 方法写入 temp;
String temp = "";
try {
// 获取 URL;
URL url2 = new URL(url1);
// 打开流,准备开始读取数据;
is = url2.openStream();
// 将流包装成字符流,调用 br.readLine() 可以提高读取效率,每次读取一行;
br = new BufferedReader(new InputStreamReader(is));
// 读取数据, 调用 br.readLine() 方法每次读取一行数据, 并赋值给 temp, 如果没数据则值 ==null,
// 跳出循环;
while ((temp = br.readLine()) != null) {
// 将 temp 的值追加给 html, 这里注意的时 String 跟 StringBuffer
// 的区别前者不是可变的后者是可变的;
html.append(temp);
}
// 接下来是关闭流, 防止资源的浪费;
if (is != null) {
is.close();
is = null;
}
// 通过 Jsoup 解析页面, 生成一个 document 对象;
Document doc = Jsoup.parse(html.toString());
// 通过 class 的名字得到(即 XX), 一个数组对象 Elements 里面有我们想要的数据, 至于这个 div的值,打开浏览器按下 F12 就知道了;
Elements elements = doc.getElementsByClass("xx");
for (Element element : elements) {
// 打印出每一个节点的信息; 选择性的保留想要的数据, 一般都是获取个固定的索引;
System.out.println(element.text());
}
} catch (MalformedURLException e) {
e.printStackTrace();
} catch (IOException e) {
e.printStackTrace();
}
}
}
代码学习中的问题和解决过程
- 问题1:计算出度和入度时,0总是多出很多,为什么?
- 问题1解决方案:
- 因为该并未初始化,所以没有的点都默认为0,于是
for(i=0;i<5;i++){
for(j=0;j<5;j++){
a[i]=0;
b[i]=0;
dig[i][j]=-1;
}
}
-
问题2:输入点不能溢出,如下图:

-
问题2解决方案:
for(i=0;i<5;i++){
System.out.println("请输入第一个: ");
int input0 = scan.nextInt();
dig[i][j] = input0;
for(j=1;;j++){
System.out.println("请问是否有下一个接点 ");
String kong = scan.nextLine();
char yn = scan.next().charAt(0);
if(('Y' == yn)||(yn == 'y')){
String kong2 = scan.nextLine();
int input = scan.nextInt();
dig[i][j] = input;
a[i]++;
}
else{
j=0;
break;
}
}
}
for(int k=0;k<5;k++) {
for(j=0;j<5;j++){
for(i=0;dig[j][i]!=-1;i++){
if(dig[j][i]==k)
b[k]++;
}
}
}
- 问题3:
- 问题3解决方案:
//java语言
public class PrintBinaryTree {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static void printTree(Node head) {
System.out.println("Binary Tree:");
printInOrder(head, 0, "H", 17);
System.out.println();
}
public static void printInOrder(Node head, int height, String to, int len) {
if (head == null) {
return;
}
printInOrder(head.right, height + 1, "v", len);
String val = to + head.value + to;
int lenM = val.length();
int lenL = (len - lenM) / 2;
int lenR = len - lenM - lenL;
val = getSpace(lenL) + val + getSpace(lenR);
System.out.println(getSpace(height * len) + val);
printInOrder(head.left, height + 1, "^", len);
}
public static String getSpace(int num) {
String space = " ";
StringBuffer buf = new StringBuffer("");
for (int i = 0; i < num; i++) {
buf.append(space);
}
return buf.toString();
}
public static void main(String[] args) {
Node head = new Node(1);
head.left = new Node(-222222222);
head.right = new Node(3);
head.left.left = new Node(Integer.MIN_VALUE);
head.right.left = new Node(55555555);
head.right.right = new Node(66);
head.left.left.right = new Node(777);
printTree(head);
head = new Node(1);
head.left = new Node(2);
head.right = new Node(3);
head.left.left = new Node(4);
head.right.left = new Node(5);
head.right.right = new Node(6);
head.left.left.right = new Node(7);
printTree(head);
head = new Node(1);
head.left = new Node(1);
head.right = new Node(1);
head.left.left = new Node(1);
head.right.left = new Node(1);
head.right.right = new Node(1);
head.left.left.right = new Node(1);
printTree(head);
}
}
总代码
代码托管第十九章
书本代码第十九章
(statistics.sh脚本的运行结果截图)

上周考试错题总结
最近无检测,故无错题
点评过的同学博客和代码
- 本周结对学习情况
- 20182326
- 结对照片


- 结对学习内容
- 学习图的定义
- 学习图的遍历
- 上周博客互评情况
其他(感悟、思考等,可选)
团队是重要,合作起来我们可以攻克所有难关。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 69/69 | 2/2 | 30/30 | Scanner |
| 第二、三周 | 529/598 | 3/5 | 25/55 | 部分常用类 |
| 第四周 | 300/1300 | 2/7 | 25/80 | junit测试和编写类 |
| 第五周 | 2665/3563 | 2/9 | 30/110 | 接口与远程 |
| 第六周 | 1108/4671 | 1/10 | 25/135 | 多态与异常 |
| 第七周 | 1946/6617 | 3/13 | 25/160 | 栈、队列 |
| 第八周 | 831/7448 | 1/14 | 25/185 | 查找、排序 |
| 第九周 | 6059/13507 | 3/17 | 35/220 | 二叉查找树 |
| 第十周 | 1354/14861 | 3/20 | 45/265 | 图 |
尝试一下记录「计划学习时间」和「实际学习时间」,到期末看看能不能改进自己的计划能力。这个工作学习中很重要,也很有用。
耗时估计的公式:Y=X+X/N ,Y=X-X/N,训练次数多了,X、Y就接近了。
-
计划学习时间:30小时
-
实际学习时间:45小时
-
改进情况:
这周没有太多别的事情,专心学习Java,攻读数据结构。



