20182301 2019-2020-1 《数据结构与面向对象程序设计》第9周学习总结

20182301 2019-2020-1 《数据结构与面向对象程序设计》第9周学习总结

教材学习内容总结

第十六章

• 树的定义

  • 根节点：唯一
  • 节点的度：节点拥有的子树数。度为0：称为终端节点或叶节点
  • 树的度：树内各节点的度的最大值
  • 内部节点：除根节点外的节点
  • 孩子（child）：节点的子树的根 称为该节点的孩子，反过来，称为双亲（parent）
  • 兄弟（sibling）：同一双亲的孩子之间的关系
  • 节点的祖先：从根到该节点所经分支上的全部节点
  • 节点层次：根为第一层，根的孩子为第二层
  • 树的深度（Depth）：树中节点的最大层次
  • 森林（Forest）：是m（m>0）棵互不相交的树的集合
    

• 树的分类

  • 满二叉树
    • 如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。
    • 如果一个二叉树的层数为K，且结点总数是(2^k) -1，则它就是满二叉树。
  • 完全二叉树
    • 它是由满二叉树而引出来的。
    • 若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，
  • 线索二叉树
    • n个结点的二叉链表中含有n+1(2n-(n-1)=n+1)个空指针域(就是用于指向左右孩子的域)。
    • 利用二叉链表中的空指针域，存放指向结点在某种遍历次序下的前驱和后继结点的指针（这种附加的指针称为"线索"）。
    • 加上线索的二叉树称为线索二叉树。
  • 哈夫曼树（霍夫曼树）又称为最优树
    • 一种带权路径长度最短的二叉树。
  • AVL树
    • 一棵空树或它的左右两个子树的高度差的绝对值不超过1
    • 左右两个子树都是一棵平衡二叉树。
  • B 树
    • 所有叶节点在同一层
    • 所有节点都存储数据
  • 2-3 树
    • 是 3 阶的 B 树
    • 是对二叉树的扩展，其中只有 2 节点和 3 节点
    • 有 2 个子节点的节点叫 2 节点，有 3 个子节点的节点叫 3 节点
    • 2 节点要么有 2 个子节点，要么没有子节点，3 节点要么有 3 个子节点，要么没有子节点
  • 2-3-4 树同理
    • 是 4 阶的 B 树
  • B+ 树
    • 是 B 树的变形
    • 非叶节点只存储索引信息，不存储数据
    • 叶子节点最右边的指针指向下一个相邻的叶节点
    • 所有的叶节点组成了一个有序链表

• 树的遍历

• 前序遍历：从根结点开始，访问每一个结点及其孩子。(A->B->D->E->C)

Visit node   
Traverse(left child) 
Traverse(right child)

• 中序遍历：从根结点开始，访问结点的左侧孩子，然后是该结点，再然后是任何剩余的结点。(D->B->E->A->C)

Traverse(left child) 
Visit node 
Traverse(right child)

• 后序遍历：从根结点开始，访问结点的孩子，然后是该结点。(D->E->B->C->A)

Traverse(left child) 
Traverse(right child) 
Visit node

• 层序遍历：从根节点开始，访问每一层的所有结点，一次一层。(A->B->C->D->E)

• 数组与链

  • 计算策略：对某些特定类型的树，特别是二叉树而言，二叉树的存储设从0开始，左子树为（2n+1），右子树为(2n+2).但是，会浪费大量的存储空间，最好用于满树。
  • 模拟链接策略：每一个结点存储的将是每一个孩子（可能还有双亲）的数组索引，而不是指向其孩子（可能还有双亲）的指针对象的引用变量，但是该方式增加了删除树中元素的成本。 模拟链接策略允许连续分配数组位置而不用考虑树的完全性。

• 决策树（详细介绍可以看实验八）

  • 过程：确定各个节点的过程，什么样的节点是最优的节点？答案是纯度最高的节点：即节点下的样本类别保持一致。
  • 定义：采用“分而治之”的思想对数据进行分类的一种算法，其形式类似于一棵树，由根节点、内部节点、叶子节点三部分组成。
  • 目前决策树常用的选择标准有3个：信息增益、信息增益率、基尼指数。

第十七章

• 二叉查找树（binary search tree）：二叉树定义的扩展，一种带有附加属性的二叉树。附加属性是什么？树中的每个节点，其左孩子都要小于其父节点，而父节点又小于或等于其右孩子。

• 二叉查找树的类图结构
  

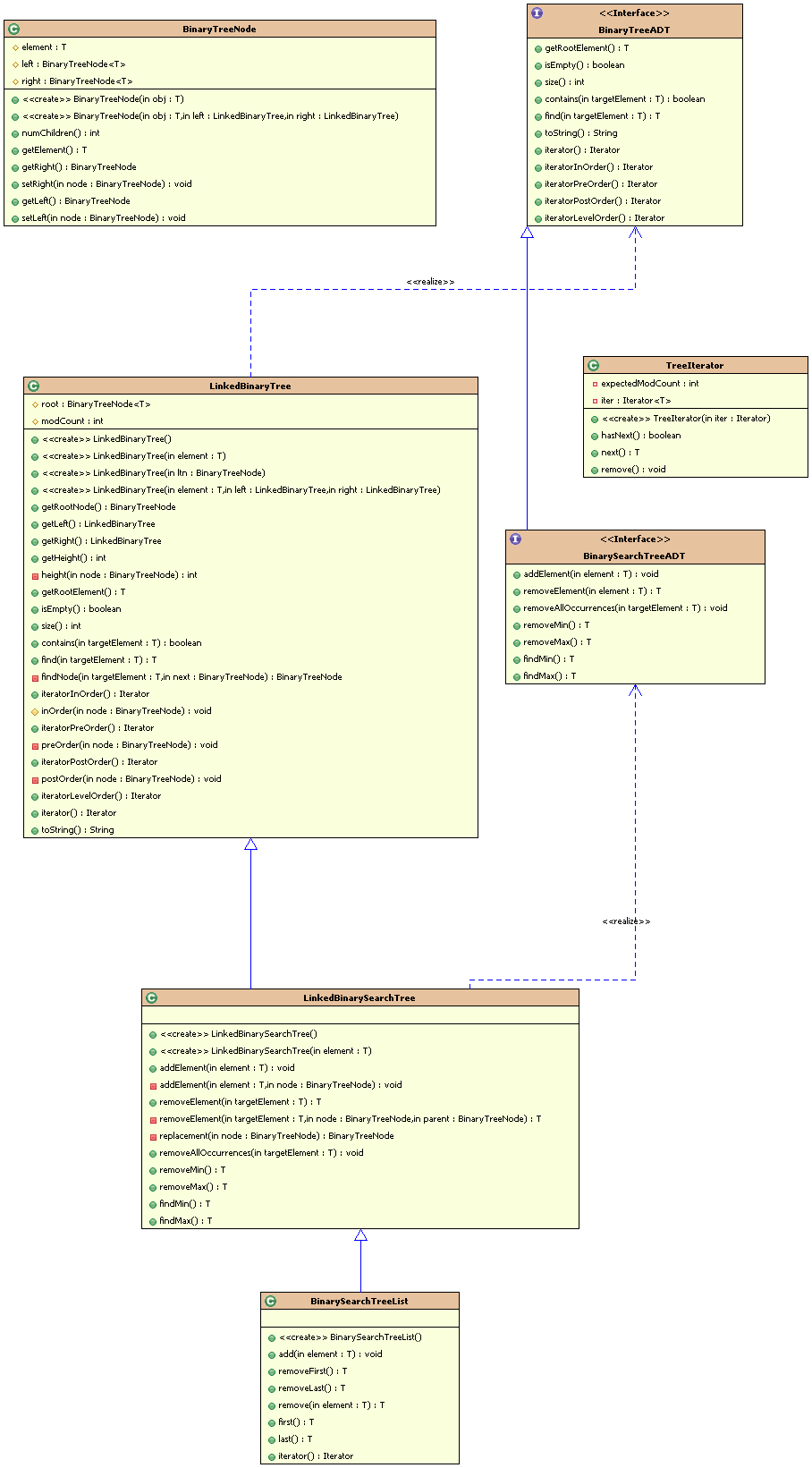
• 二叉查找树涉及到的基本方法

• addElement（元素添加）操作

  • addElement根据方法给定的元素的值，在树中的恰当的位置添加该元素。
  • 如果这个元素不是Comparable,则addElement方法会抛出一个NonComparableElementException("LinkedBinarySearchTree")
  • 如果树为空，那么新元素就会称为根结点，如果不为空，如果小于则 在左边递归；大于等于，则在右边递归。

public void addElement(T element) {
        if (!(element instanceof Comparable)) {
            throw new NonComparableElementException("LinkedBinarySearchTree");
        }

        Comparable<T> comElem = (Comparable<T>) element;
        if (isEmpty()) {
            root = new BinaryTreeNode<T>(element);
        } else {
            if (comElem.compareTo(root.getElement()) < 0) {
                if (root.getLeft() == null) {
                    this.getRootNode().setLeft(new BinaryTreeNode<T>(element));
                } else {
                    addElement(element, root.getLeft());
                }
            } else {
                if (root.getRight() == null) {
                    this.getRootNode().setRight(new BinaryTreeNode<T>(element));
                } else {                   addElement(element, root.getRight());
                }
            }
        }
        modCount++;
    }

• removeElement（删除元素）操作
  • 负责从二叉查找树中删除给定的comparable元素；或者当在树中找不到给定的目标元素时，则抛出ElementNotFoundException异常。
  • 与前面的线性结构研究不同，这里不能通过简单的通过删除指定结点的相关引用指针而删除该结点。相反这里必须推选出一个结点来取代要被删除的结点。
  • 受保护方法，replacement返回指向一个结点的应用，该结点将代替要删除的结点，选择替换结点有三种情况：
    • 如果被删除结点没有孩子那么repalcement返回null
    • 如果有一个，那么replacement返回这个孩子
    • 如果有两个孩子，则replacement会返回终须后继者。因为相等元素会放在后边

public T removeElement(T targetElement) {

        T result = null;
        if (isEmpty()) {
            throw new ElementNotFoundException("LinkedbinarySearchTree");
        } else {
            BinaryTreeNode<T> parent = null;
            if (((Comparable<T>) targetElement).equals(root.getElement())) {
                result = root.element;
                BinaryTreeNode<T> temp = replacement(root);

                if (temp == null) {
                    root = null;
                } else {

                    root.element = temp.element;
                    root.setLeft(temp.getLeft());
                    root.setRight(temp.getRight());

                }
                modCount--;

            } else {
                parent = root;
                if (((Comparable<T>) targetElement)
                        .compareTo(root.getElement()) < 0) {
                    result = removeElement(targetElement, root.getLeft(),
                            parent);
                } else {
                    result = removeElement(targetElement, root.getRight(),
                            parent);
                }
            }

        }

        return result;
    }

private BinaryTreeNode<T> replacement(BinaryTreeNode<T> node) {
        BinaryTreeNode<T> result = null;
        if ((node.left == null) && (node.right == null)) {
            result = null;
        } else if ((node.left != null) && (node.right == null)) {
            result = node.left;

        } else if ((node.left == null) && (node.right != null)) {
            result = node.right;
        } else {
            BinaryTreeNode<T> current = node.right;// 初始化右侧第一个结点
            BinaryTreeNode<T> parent = node;

            // 获取右边子树的最左边的结点
            while (current.left != null) {
                parent = current;
                current = current.left;
            }

            current.left = node.left;

            // 如果当前待查询的结点
            if (node.right != current) {
                parent.left = current.right;// 整体的树结构移动就可以了
                current.right = node.right;
            }

            result = current;
        }
        return result;
    }

• removeAllOccurrences（删除指定元素）操作
  • 负责从二叉查找树中删除指定元素的所有存在;或者，当先在树中找不到指定元素的时候，抛出ElementNotFoundException异常。
  • 如果指定元素不是com类型 则抛出class异常。

public void removeAllOccurrences(T targetElement) {
        removeElement(targetElement);

        try {
            while (contains((T) targetElement))
                removeElement(targetElement);
        }

        catch (Exception ElementNotFoundException) {
        }

    }

• findMin（找到最小值）操作
• 我认为findMin、findMax、removeMax、removeMin有异曲同工之妙，故在这里只介绍findMin。
• 最小元素在二叉查找树的可能情况：
  • 树根没有左孩子，树根即为最小元素；
  • 树的最左侧结点为一片叶子，该叶子即为最小元素；
  • 树的最左侧结点为内部结点。
• 这几种来进行寻找

public T findMin() {
        T result = null;

        if (isEmpty())
            throw new EmptyCollectionException("LinkedBinarySearchTree");
        else {
            if (root.left == null) {
                result = root.element;
                //root = root.right;
            } else {
                BinaryTreeNode<T> parent = root;
                BinaryTreeNode<T> current = root.left;
                while (current.left != null) {
                    parent = current;
                    current = current.left;
                }
                result = current.element;
                //parent.left = current.right;
            }

            //modCount--;
        }

        return result;
    }

• 用链表实现二叉查找树

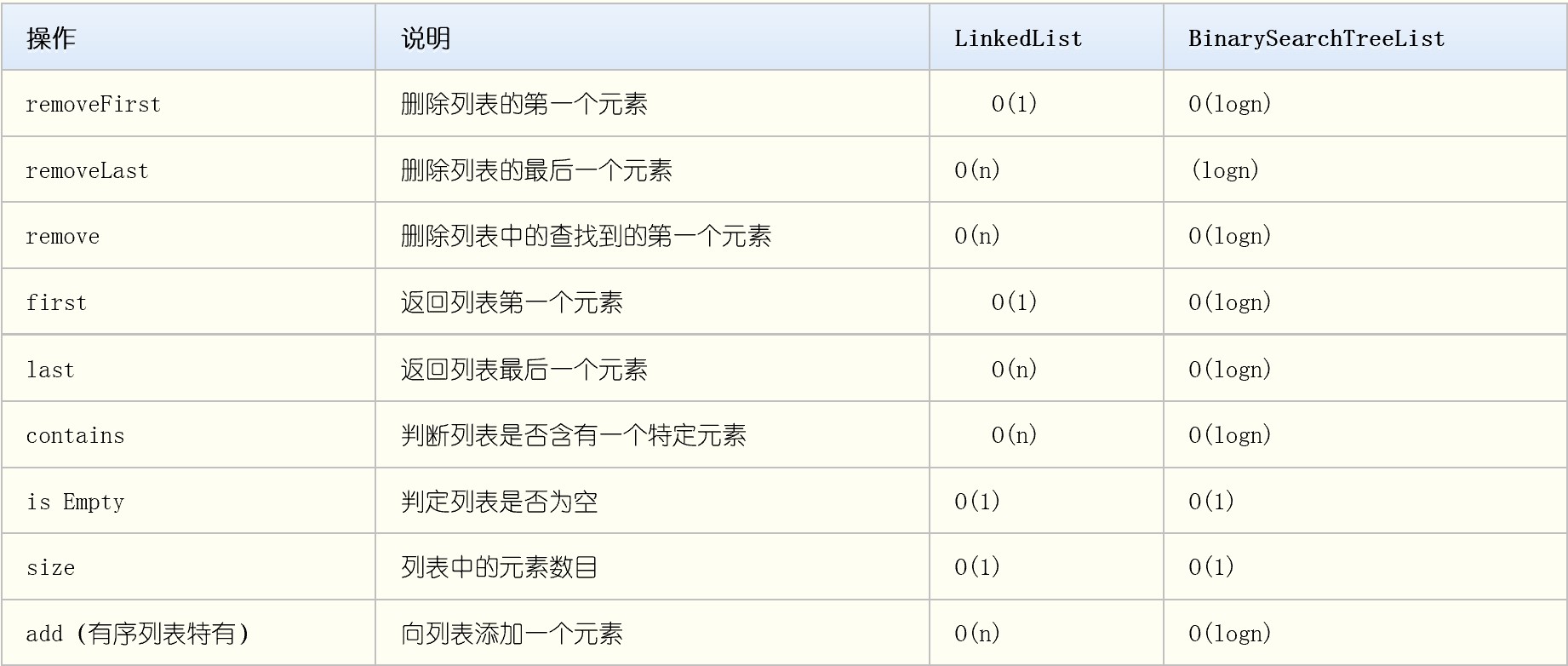
• 平衡二叉查找树
• 1962年，Adelson-Velsikii和Landis提出了一种结点在高度上相对平衡的二叉查找树，又称为AVL树。其平均和最坏情况下的查找时间都是O(logn)。同时，插入和删除的时间复杂性也会保持O(logn)。平衡二叉树的定义如下:
  • 它或者是一棵空二叉树。
  • 或者是具有如下性质的二叉查找树：其左子树和右子树都是高度平衡的二叉树，且左子树和右子树的高度之差的绝对值不超过1。
• 如果将二叉树上结点的平衡因子BF（Balanced Factor）定义为该结点的左子树与右子树的高度之差，根据AVL树的定义，AVL树中的任意结点的平衡因子只可能是-1（右子树高于左子树）、0或者1（左子树高于右子树）。
• 旋转方式
• 右旋转
  

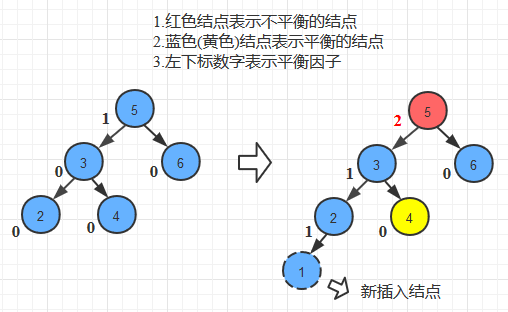
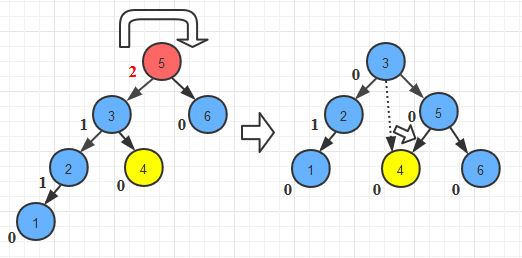
//RR旋转

public AVLTreeNode singleRotateRight(AVLTreeNode w){

    AVLTreeNode x=  w.getRight();

    w.setRight(x.getLeft());

    x.setLeft(w);

    w.setHeight(Math.max(Height(w.getRight()),Height(w.getLeft()))+1);

    x.setHeight(Math.max(Height(x.getRight()),w.getHeight())+1);

    return x;

}

• 左旋转

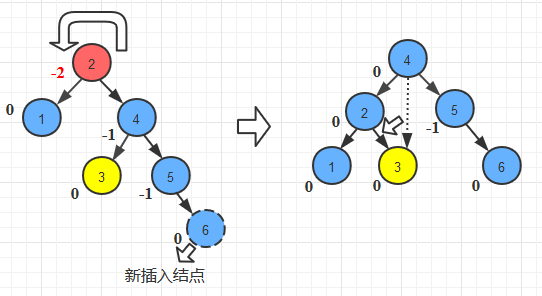
//LL旋转

public AVLTreeNode singleRotateLeft(AVLTreeNode x){

    AVLTreeNode w=  x.getLeft();

    x.setLeft(w.getRight());

    w.setRight(x);

    x.setHeight(Math.max(Height(x.getLeft()),Height(x.getRight()))+1);

    w.setHeight(Math.max(Height(w.getLeft()),x.getHeight())+1);

    return w;

}

• 左右旋转：首先将失衡节点的左子树进行左旋，然后对以失衡节点为根节点的树进行右旋
  

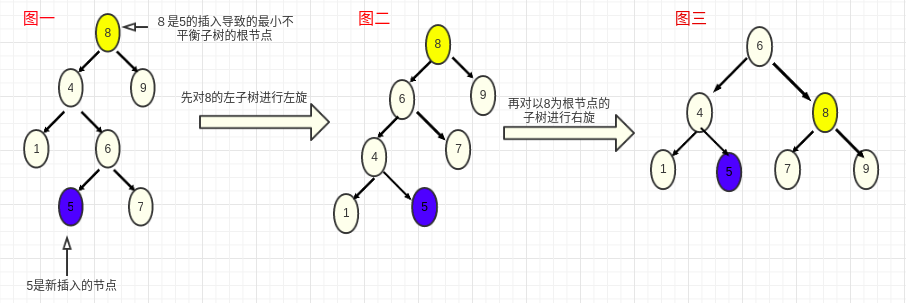
//LR旋转

public AVLTreeNode doubleRotateLeft(AVLTreeNode z){

    z.setLeft(singleRotateRight(z.getLeft()));//在X和Y之间旋转

    return singleRotateLeft(z);//在Z和Y之间旋转

}

• 右左旋转：插入节点出现在离他最近的失衡节点的右孩子的左子树上

public AVLTreeNode doubleRotateRight(AVLTreeNode x){    
x.setRight(singleRotateRight(x.getLeft()));//在Z和Y之间旋转    
return singleRotateRight(x);//在X和Y之间旋转}

• 再平衡的判断：根据当前破坏平衡的结点的平衡因子，以及其孩子结点的平衡因子来判定，通过旋转来调整。
  
  

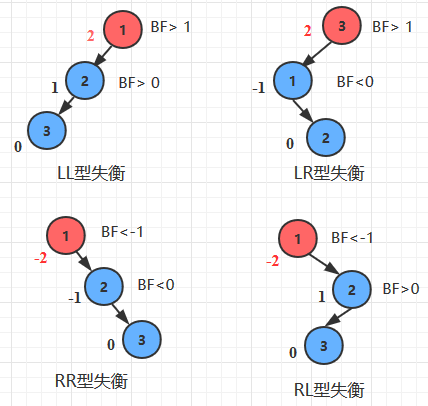
教材学习中的问题和解决过程

• 问题1：为什么要将二叉查找树进行平衡?如果不平衡,会出现什么情况?
• 问题1解决方案：（详见链接4）
• AVL树是一种自平衡的二叉搜索树，在进行动态操作时可以维持自身形态的平衡，从而保证基本操作的时间复杂度维持在O(logn)。
• 下图为一个低效的二叉查找树的示意图，它已经退化成了链表，完全失去了二叉查找树的优势

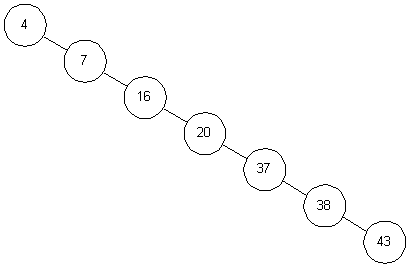
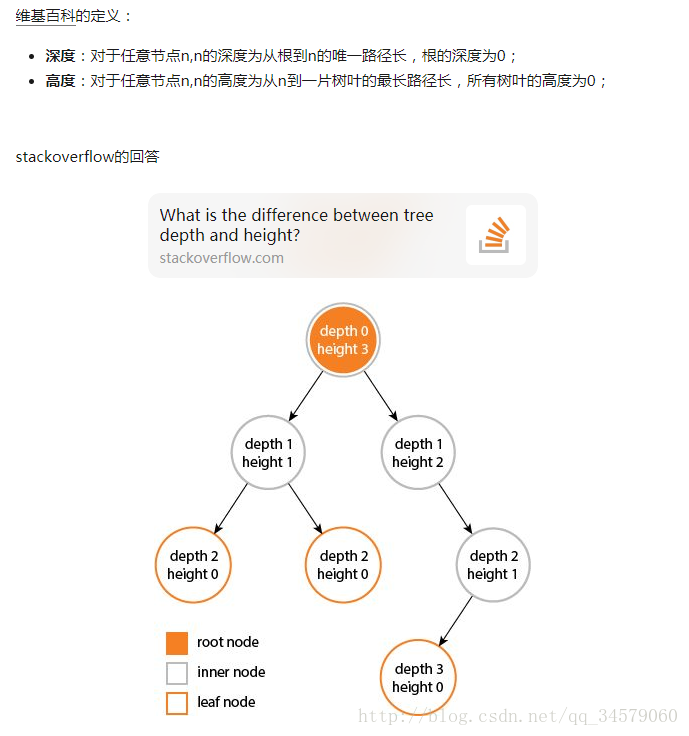
• 问题2：高度和深度的区别是什么？

• 问题2解决方案：（图）
  

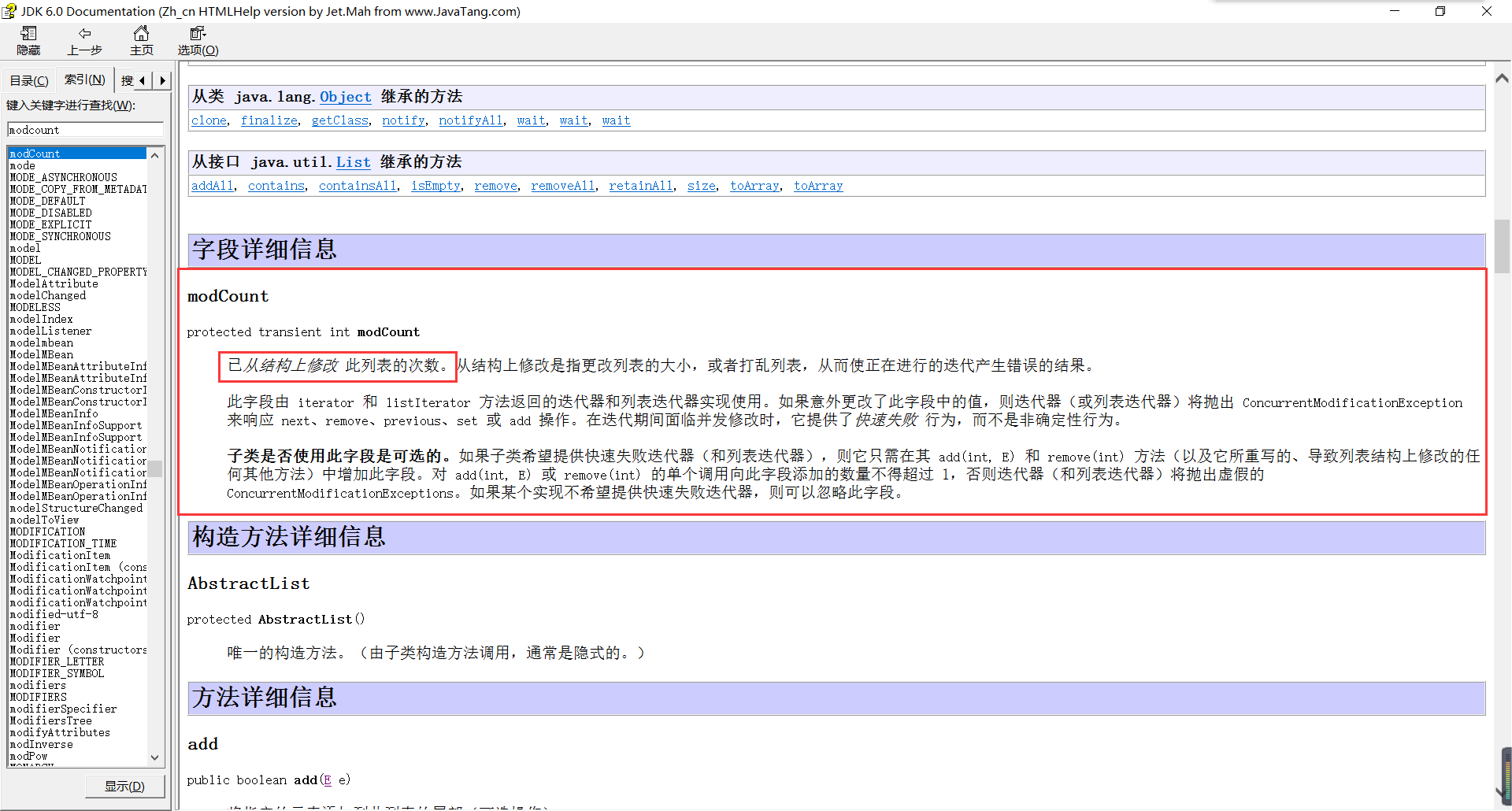
• 问题3：变量modCount是什么意思？

• 问题3解决方案：（图）

• 问题4：决策树涉及到的三个标准，我还不太理解（详见链接6）
• 问题4解决方案：
• 信息增益

  • 通常使用“熵”来度量样本集合的纯度，“熵”就是物体内部的混乱程度，理论上“熵”的值越小，数据集的“纯度”越高，下面是“熵”的计算公式：
    

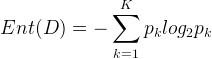
  • Pk指的是第k类样本所占的比率。

  • 信息增益，指的是测试属性对于样本纯度的增益效果，值越大越好，计算公式为：
    

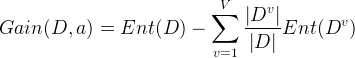
  • 信息增益=样本的熵-所有测试属性熵的和

  • Dv指的是满足某个测试属性的样本集。

  • 选择信息增益最大的属性，作为根节点，然后递归计算最优的节点属性即可组成最优的策略树。ID3算法就是依此实现的。

• 信息增益率

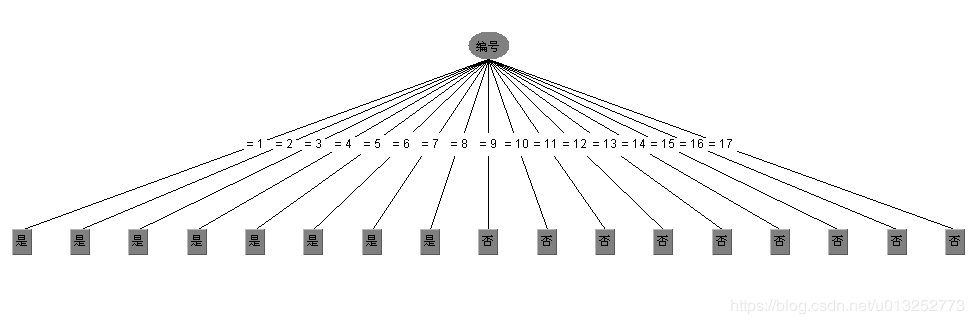
  • 当样本数据中存在ID类型的数据时，由于每条数据的id都不一样，这样id属性对应的熵值是最小的，即纯度是最高的，信息增益是最大的，但是显而易见以id作为根节点是不合适的，这样就会变成一颗只有2层的“宽”树，不具备泛化的能力：
    

  • 为了解决这个问题，提出了信息增益率的概念。
    

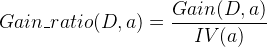
  • 其中：
    

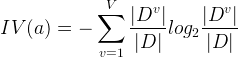
  • v是属性a的可能取值，v越小则IV(a)越小，信息增益率越大。

• 基尼指数

  • 基尼指数是另一个选择的标准，代表了从样本中任意选择两个样本，类别不一致的概率，所以基尼指数越小，代表样本纯度越高。
    

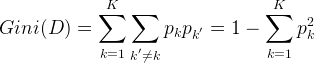
  • 属性a的基尼指数定义为属性a各类样本比率的基尼指数和：
    

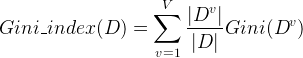
代码调试中的问题和解决过程

• 问题1：instanceof第一次遇见，需要了解一下
• 问题1解决方案：（详见链接2）
• 定义：instanceof是Java中的二元运算符，左边是对象，右边是类；当对象是右边类或子类所创建对象时，返回true；否则，返回false。
• 注意：
  • 类的实例包含本身的实例，以及所有直接或间接子类的实例
  • instanceof左边显式声明的类型与右边操作元必须是同种类或存在继承关系，也就是说需要位于同一个继承树，否则会编译错误
• instanceof用法

  • 左边的对象实例不能是基础数据类型
    

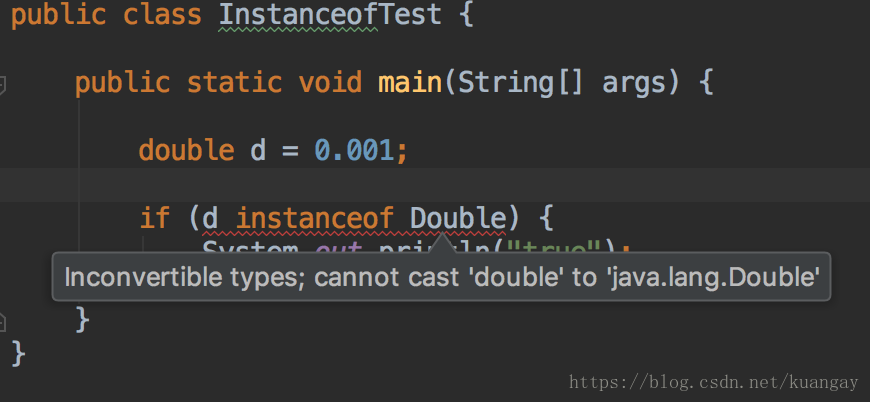
  • 左边的对象实例和右边的类不在同一个继承树上
    

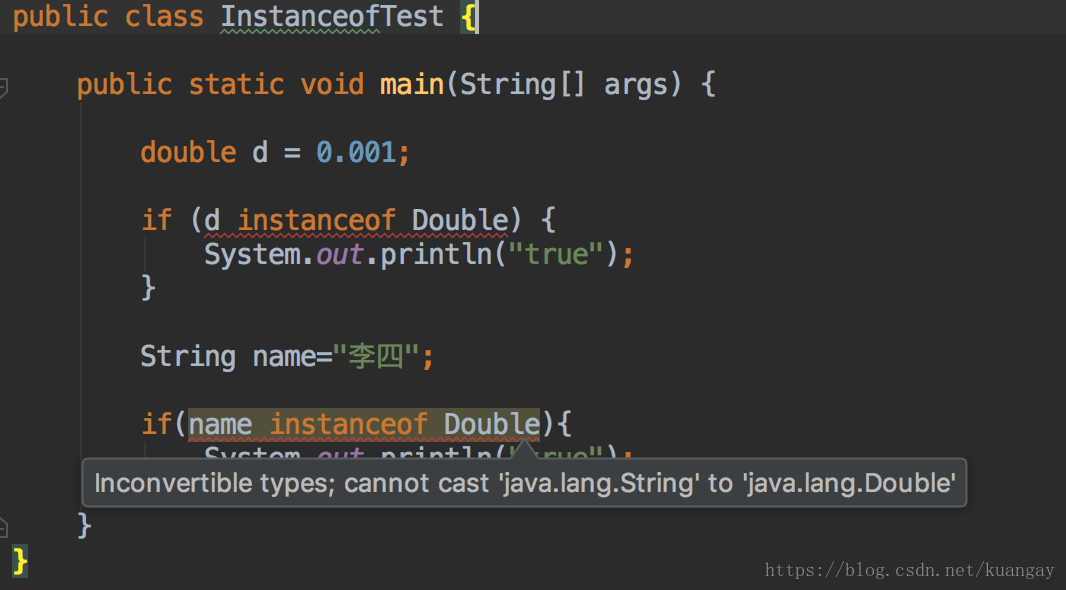
  • null用instanceof跟任何类型比较时都是false
    

  • 运行结果：

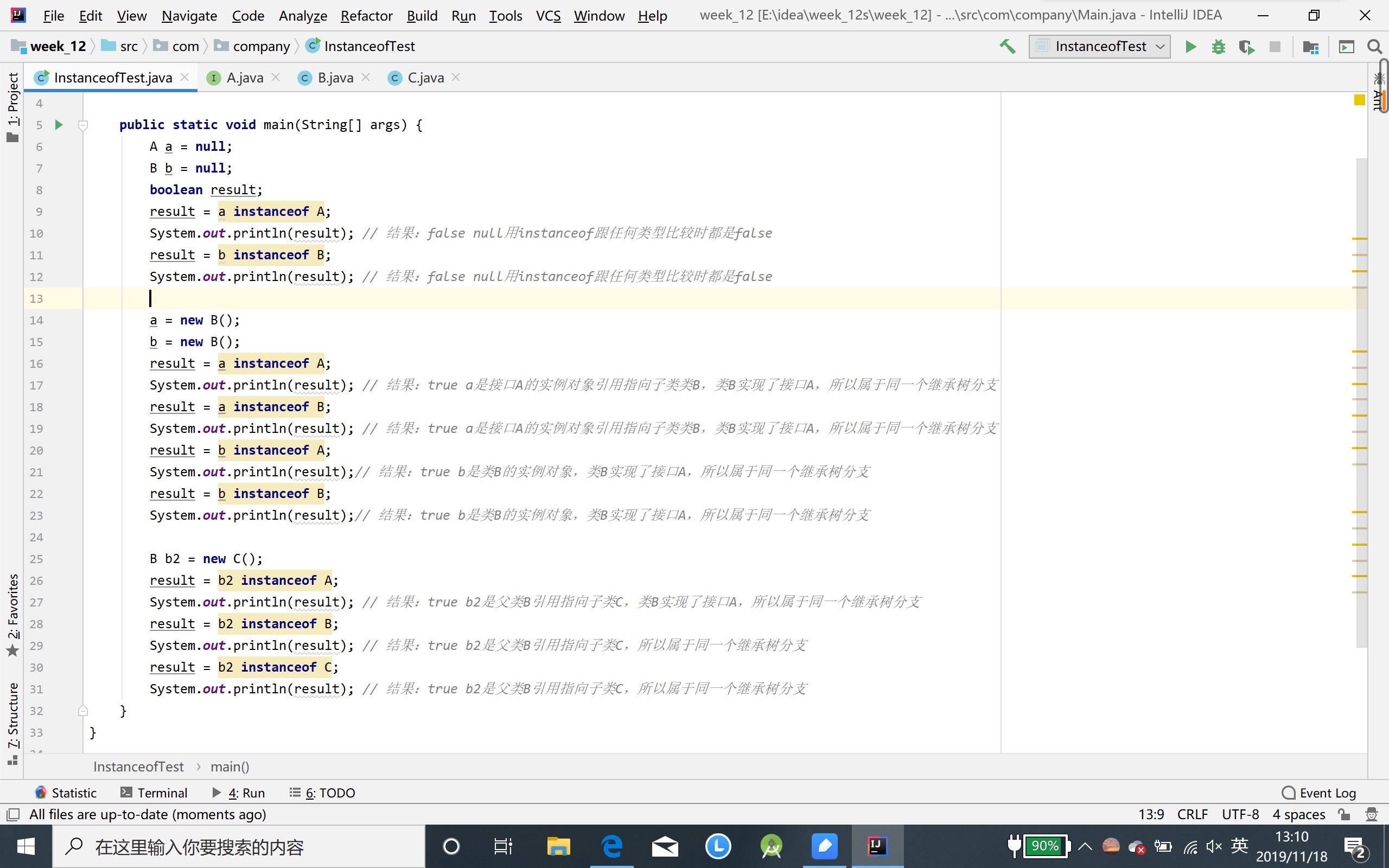
• instanceof一般用于对象类型强制转换
• 问题2：有序链表转换平衡二叉树
• 问题2解决方案：（详见链接3）

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}
class ListNode {
    int val;
    ListNode next;
    ListNode(int val) { this.val = val;}
}
class Solution {
    public TreeNode sortedListToBST(ListNode head) {
        if(head == null) return null;
        return createTree(head, null);
    }
    public TreeNode createTree(ListNode head, ListNode tail) {
        if(head == tail ) return null;
        ListNode fast = head;
        ListNode slow = head;
        while(fast != tail && fast.next != tail) {
            fast = fast.next.next;
            slow = slow.next;
        }
        TreeNode node = new TreeNode(slow.val);
        node.left = createTree(head, slow);
        node.right = createTree(slow.next, tail);
        return node;
    }
}
public class LED {
    public static int[] stringToArrays(String input) {
        input = input.trim();
        input = input.substring(1, input.length() - 1);
        if(input == null) {
            return new int[0];
        }
        String[] patrs = input.split(",");
        int[] res = new int[patrs.length];
        for(int i = 0; i < res.length; i ++) {
            res[i] = Integer.parseInt(patrs[i].trim());
        }
        return res;
    }
    public static ListNode stringToListNode(String input) {
        int[] nodes = stringToArrays(input);
        ListNode dummpy = new ListNode(-1);
        ListNode cur = dummpy;
        for(int x : nodes) {
            cur.next = new ListNode(x);
            cur = cur.next;
        }
        return dummpy.next;
    }
    public static String treeNodeToString(TreeNode root) {
        if(root == null) {
            return "[]";
        }
        String ouput = "";
        Queue<TreeNode> nodeQueue = new LinkedList<>();
        nodeQueue.add(root);
        while(!nodeQueue.isEmpty()) {
            TreeNode node = nodeQueue.remove();
            if(node == null) {
                ouput += "null, ";
                continue;
            }
            ouput += String.valueOf(node.val) + ", ";
            nodeQueue.add(node.left);
            nodeQueue.add(node.right);
        }
        return "[" + ouput.substring(0, ouput.length() - 2) + "]";
    }
    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        String line = null;
        while((line = in.readLine()) != null) {
            ListNode head = stringToListNode(line);
            TreeNode res = new Solution().sortedListToBST(head);
            String result = treeNodeToString(res);
            System.out.println(result);
        }
    }
}

总代码

代码托管第十六章

书本代码第十六章

代码托管第十七章

书本代码第十七章

（statistics.sh脚本的运行结果截图）

上周考试错题总结

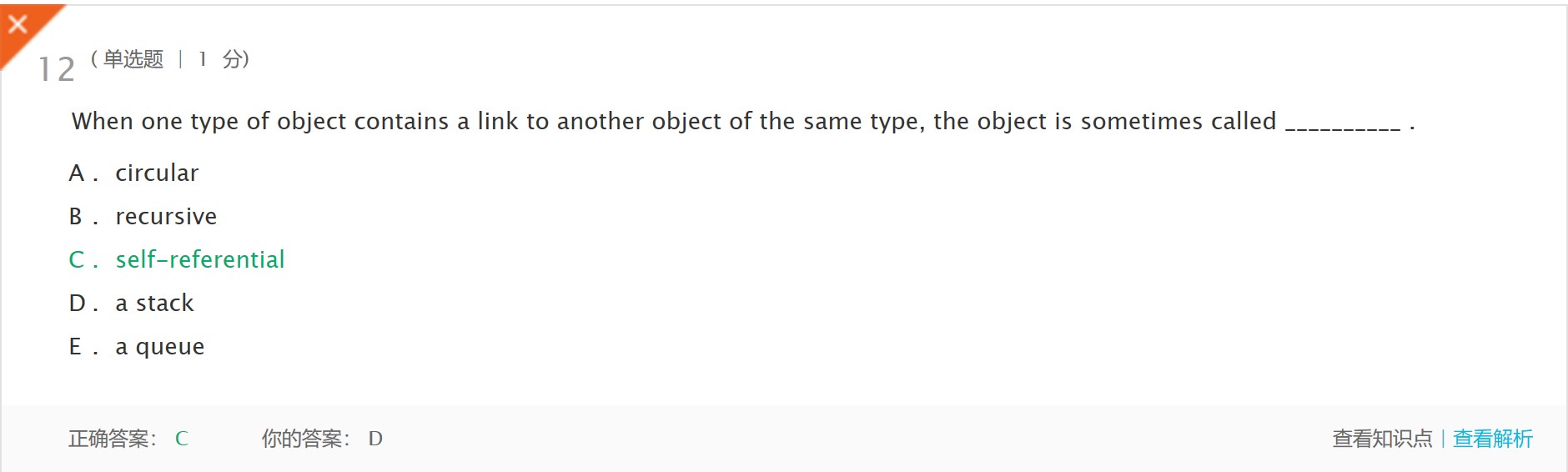
• 解析：A self-referential object is one that refers to another object of the same type.（自引用对象是指引用同一类型的另一个对象。）

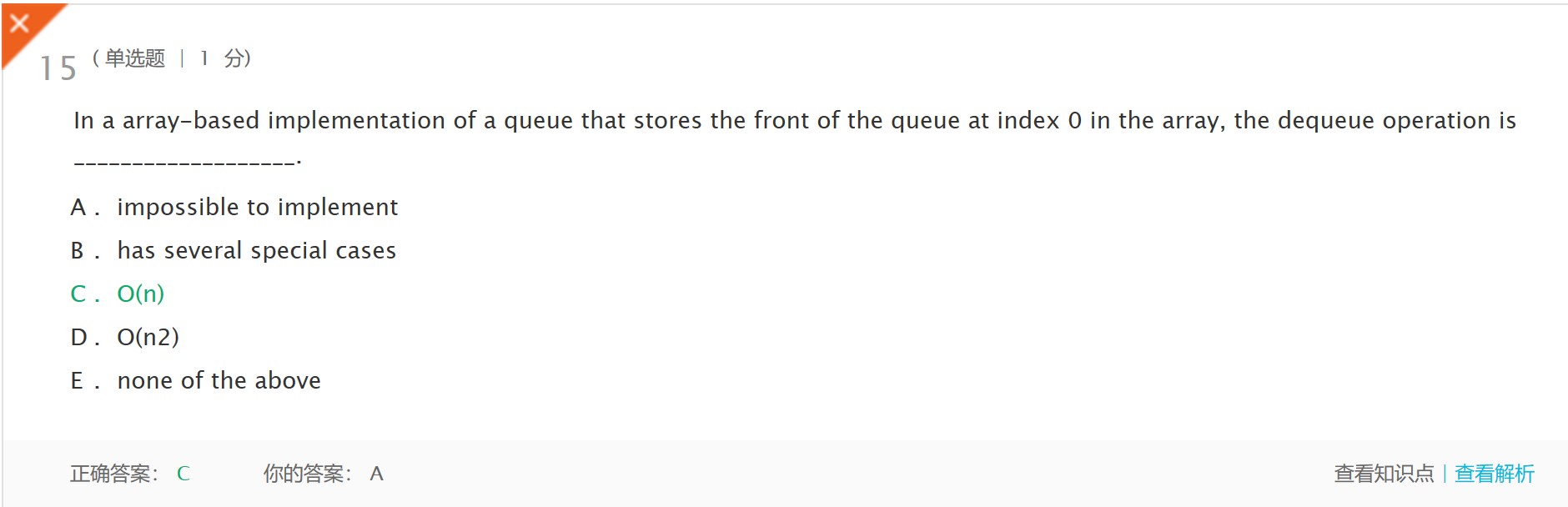
• 解析：It requires a linear amount of time to shift all elements of the queue down an index after a remove is applied（在应用了删除操作之后，需要线性时间将队列的所有元素向下移动一个索引）

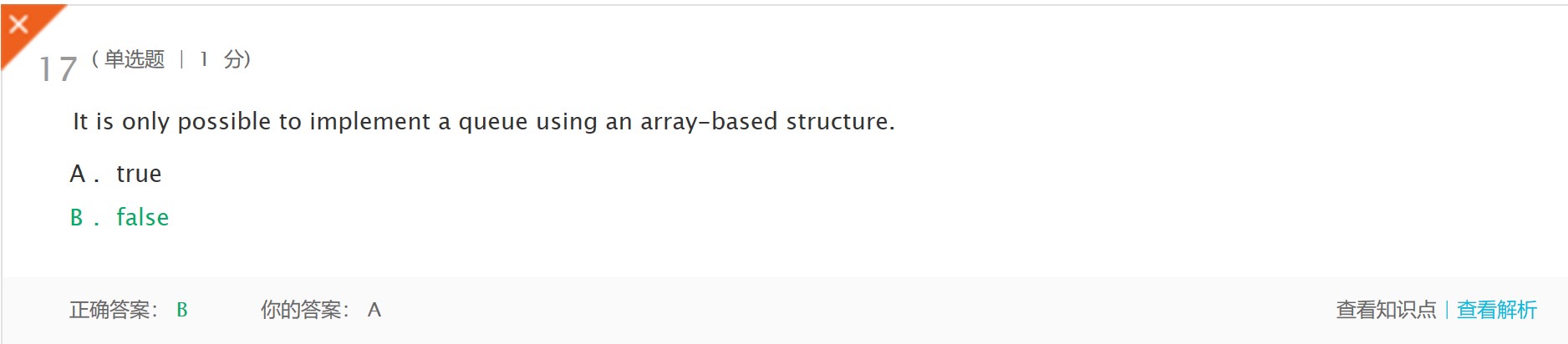
• 解析：A queue can be implemented using a linked structure or an array-based structure.（可以使用链接结构或基于数组的结构来实现队列。）

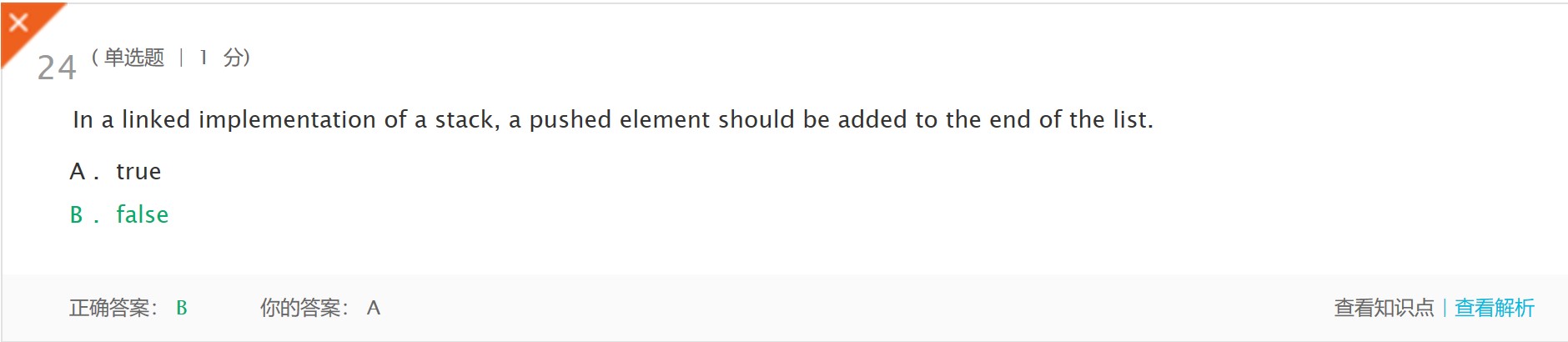
• 解析：In a linked implementation of a stack, a pushed element should be added to the front of the list. If the element is added to the end of the list, the pop operation would require linear time, because we would need to go through the entire element to get a pointer to the next-to-last element in the list.（在堆栈的链接实现中，应将推入的元素添加到列表的前面。如果元素被添加到列表的末尾，pop操作将需要线性时间，因为我们需要遍历整个元素以获得指向列表中倒数第二个元素的指针。）

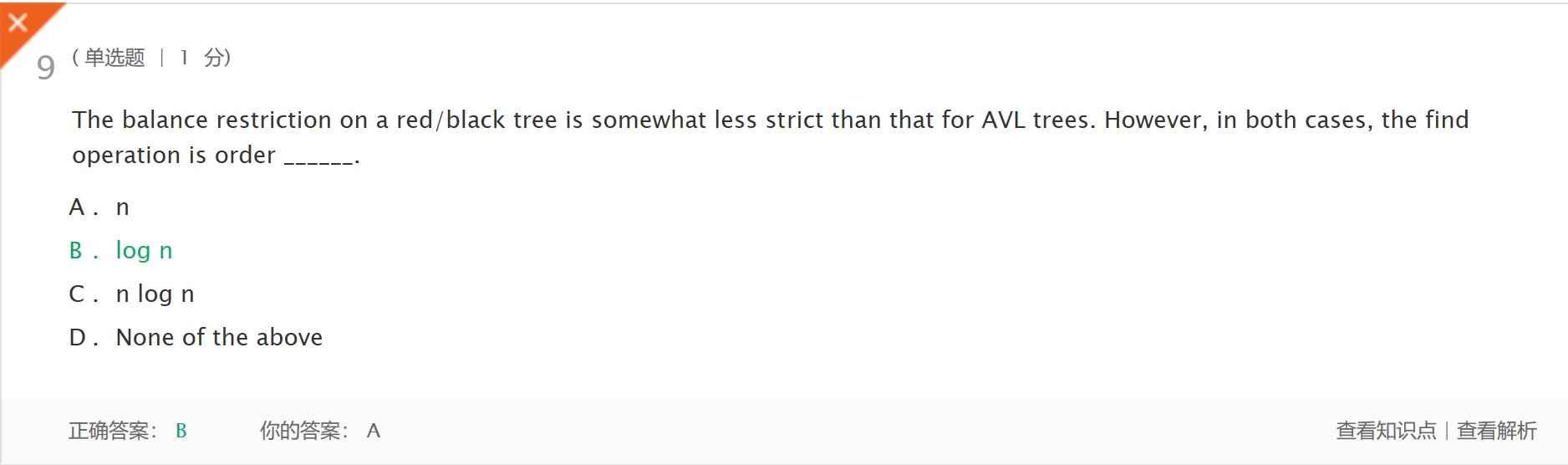
• 解析：在红/黑树上的平衡限制没有AVL树那么严格。但是，在这两种情况下，查找操作都是o (log n)

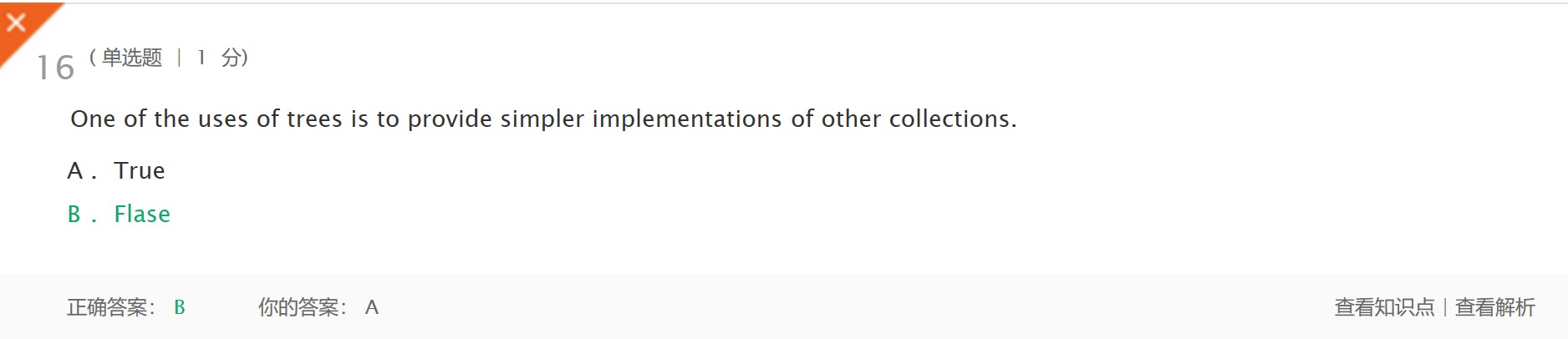
• 解析：树与线性表、栈、队列等线性结构不同，树是一种非线性结构。

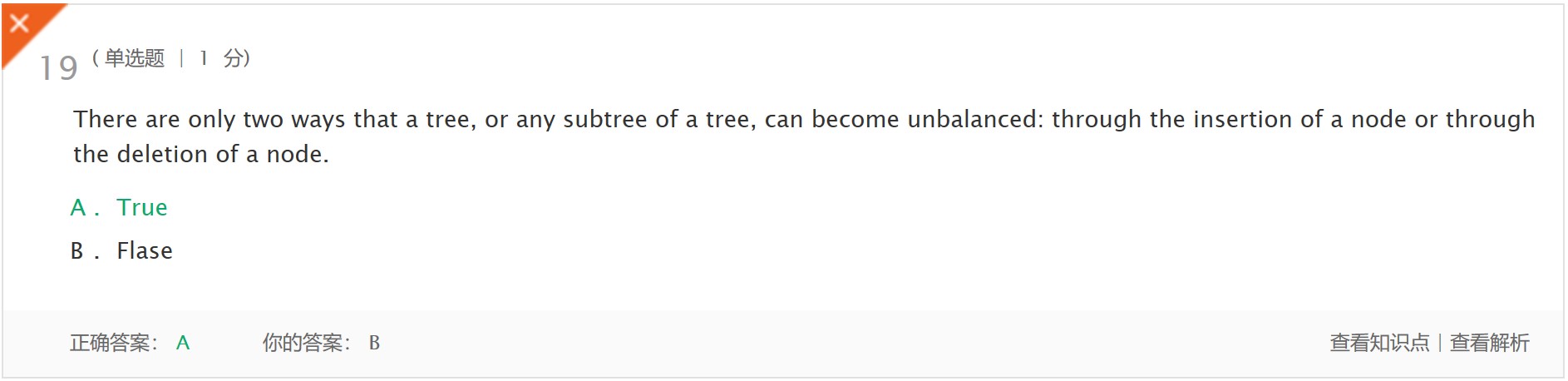
• 解析：树或树的任何子树只有两种方式会变得不平衡:通过插入节点或删除节点。

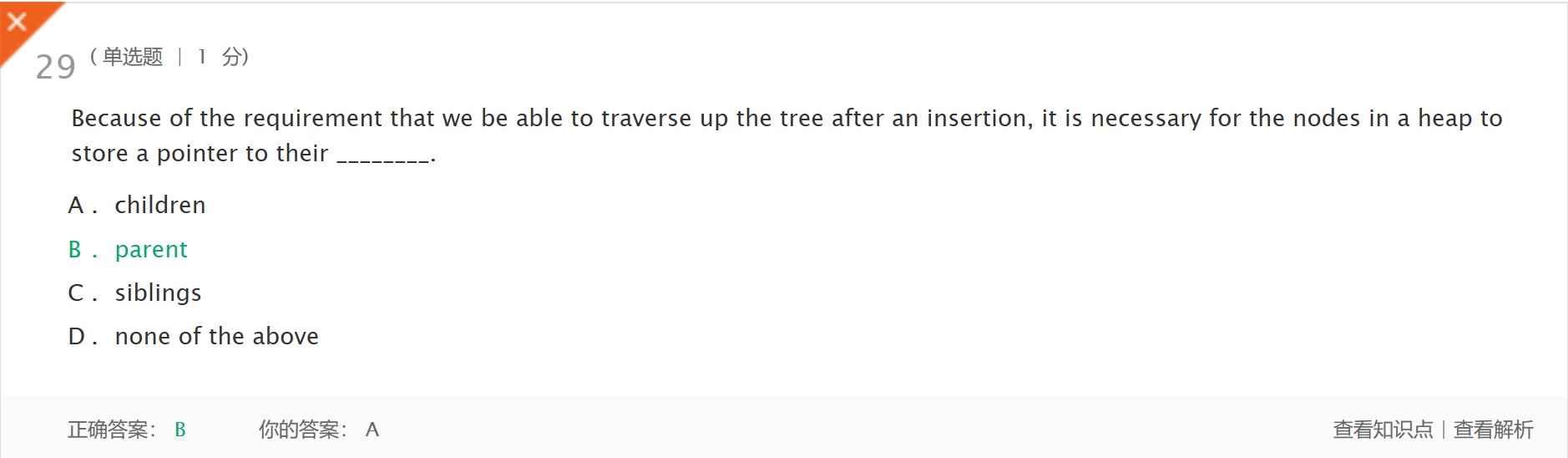
• 解析：因为我们需要在插入之后遍历树，所以堆中的节点必须存储指向它们的父母

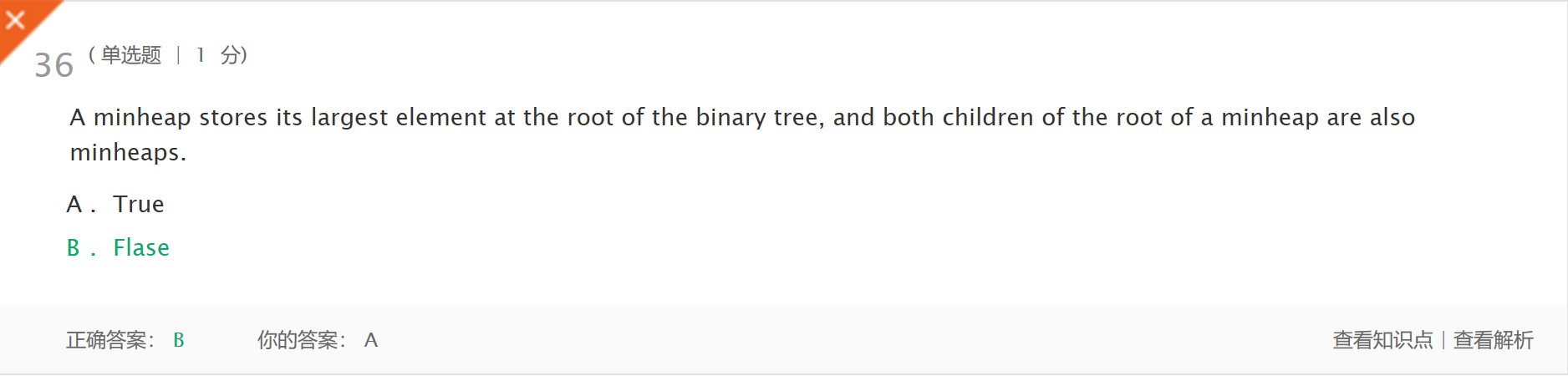
• 解析：minheap将其最大的元素存储在二叉树的根中，minheap根的两个子元素不一定是minheap。

点评过的同学博客和代码

• 本周结对学习情况
  • 20182326
  • 结对照片

- 结对学习内容
    - 学习二叉查找树
    - 学习树的基本

• 上周博客互评情况
  • 20182326

其他（感悟、思考等，可选）

这周有了更多的时间来学习数据结构，感觉有点吃力，要努力！

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	69/69	2/2	30/30	Scanner
第二、三周	529/598	3/5	25/55	部分常用类
第四周	300/1300	2/7	25/80	junit测试和编写类
第五周	2665/3563	2/9	30/110	接口与远程
第六周	1108/4671	1/10	25/135	多态与异常
第七周	1946/6617	3/13	25/160	栈、队列
第八周	831/7448	1/14	25/185	查找、排序
第九周	6059/13507	3/17	35/220	二叉查找树

尝试一下记录「计划学习时间」和「实际学习时间」，到期末看看能不能改进自己的计划能力。这个工作学习中很重要，也很有用。
耗时估计的公式：Y=X+X/N ，Y=X-X/N，训练次数多了，X、Y就接近了。

参考：软件工程软件的估计为什么这么难，软件工程 估计方法

• 计划学习时间:30小时

• 实际学习时间:35小时

• 改进情况：
  这周的别的事情较多，所以很急，以后一定好好把本次课程复习一下。

参考资料

• 数据结构（JAVA）——二叉查找树
• Java instanceof用法详解
• 有序链表转换二叉搜索树(java)
• AVL
• 平衡二叉树——AVL树的旋转操作：Java语言实现
• 决策树