机器学习中优化算法【需整理】

1、怎么证明凸函数, 二阶Hessian矩阵半正定，函数为凸函数

    证明参考：https://math.stackexchange.com/questions/946156/proving-convexity-of-a-function-whose-hessian-is-positive-semidefinite-over-a-co 

 

以简单的线性回归为例，

样本回归模型：

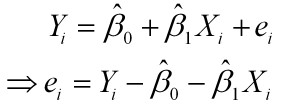
平方损失函数：

 

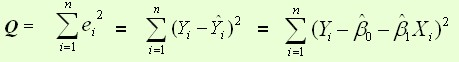
1、最小二乘法

     最小二乘法是求解令损失函数最小的参数的过程。主要就是对每个参数求导，令结果为0，所求的参数即可满足令损失函数最小

 

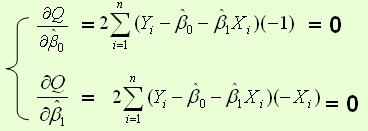
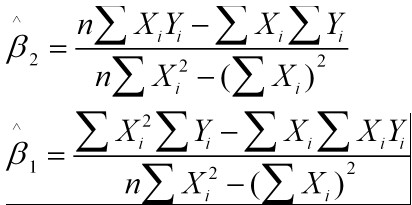
2、梯度下降

梯度下降法是一种迭代法，先给定一个，然后向下降最快的方向调整，在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢，并且对初始点的选择极为敏感，其改进大多是在这两方面下功夫。

梯度下降分为批量梯度下降、随机梯度下降和小批量梯度下降

首先当我们只有一个数据点（x,y）的时候，J的偏导数是：

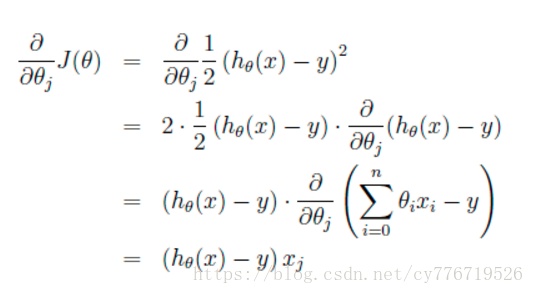
则对所有数据点，上述损失函数的偏导（累和）为：

 

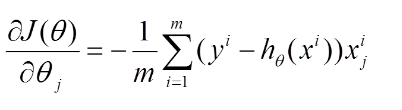
再最小化损失函数的过程中，需要不断反复的更新weights使得误差函数减小，更新过程如下：

 

三种梯度下降的python实现

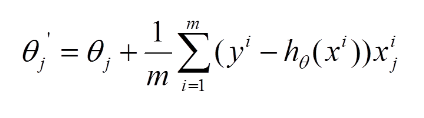
1、批量梯度下降：

     批量即选择全部样本进行迭代，当样本数很大时，将会非常慢

2、随机梯度下降：

 随机梯度下降随机选择一个样本进行迭代，容易受噪声/离群点/异常值的影响非常大，所以采用很小的learning rate

3、小批量梯度下降：

每次迭代时使用一批数据，这批数据可以自行选择也可以随机产生，大小也可自由自定，越大越接近批量梯度下降算法，越小越接近随机梯度下降算法

 

梯度下降过程中学习率是不改变的，当太大的时候可能错过最优点，当太小收敛太慢，所以产生了一种动态修改学习率的方式[Backtracking line search]，初始的学习率很大，随着不断学习，学习率慢慢减小

引用于 https://www.cnblogs.com/fstang/p/4192735.html
# -*- coding: cp936 -*-
#optimization test, y = (x-3)^2
from matplotlib.pyplot import figure, hold, plot, show, xlabel, ylabel, legend
def f(x):
        "The function we want to minimize"
        return (x-3)**2
def f_grad(x):
        "gradient of function f"
        return 2*(x-3)
x = 0
y = f(x)
err = 1.0
maxIter = 300
curve = [y]
it = 0
step = 0.1
#下面展示的是我之前用的方法，看上去貌似还挺合理的，但是很慢
while err > 1e-4 and it < maxIter:
    it += 1
    gradient = f_grad(x)
    new_x = x - gradient * step
    new_y = f(new_x)
    new_err = abs(new_y - y)
    if new_y > y: #如果出现divergence的迹象，就减小step size
        step *= 0.8
    err, x, y = new_err, new_x, new_y
    print 'err:', err, ', y:', y
    curve.append(y)

print 'iterations: ', it
figure(); hold(True); plot(curve, 'r*-')
xlabel('iterations'); ylabel('objective function value')

#下面展示的是backtracking line search，速度很快
x = 0
y = f(x)
err = 1.0
alpha = 0.25
beta = 0.8
curve2 = [y]
it = 0

while err > 1e-4 and it < maxIter:
    it += 1
    gradient = f_grad(x)
    step = 1.0
    while f(x - step * gradient) > y - alpha * step * gradient**2:
        step *= beta
    x = x - step * gradient
    new_y = f(x)
    err = y - new_y
    y = new_y
    print 'err:', err, ', y:', y
    curve2.append(y)

print 'iterations: ', it
plot(curve2, 'bo-')
legend(['gradient descent I used', 'backtracking line search'])
show()

 

3、牛顿法

牛顿法与梯度下降的对比？

参考：https://www.zhihu.com/question/19723347

牛顿法是二阶收敛，梯度下降是一阶收敛，二阶收敛要比一阶收敛快， 为什么？

我觉着可以从泰勒展开的角度来分析：当是二阶的时候表示泰勒取到了二次项，此时更接近真实的函数，所以会比取一次收敛的快

 

牛顿法迭代公式，可由泰勒展开推出

梯度下降是一种特殊的牛顿法，当海参矩阵为单位矩阵是，牛顿法就变成梯度下降了。

 

 4、拟牛顿法

 因为在牛顿法中出现了海参矩阵，这个矩阵的计算比较麻烦，所以想办法不来直接求海参矩阵，而用其他的方式来替代，也就是牛顿方法

 

参考：

http://www.hankcs.com/ml/l-bfgs.html

https://applenob.github.io/crf.html