【自然语言处理】词向量
一、词向量
词向量的表示方法:
其基本想法是:
通过训练将某种语言中的每一个词映射成一个固定长度的短向量(当然这里的“短”是相对于 one-hot representation 的“长”而言的),将所有这些向量放在一起形成一个词向量空间,而每一向量则为该空间中的一个点,在这个空间上引入“距离”,则可以根据词之间的距离来判断它们之间的(词法、语义上的)相似性了。
为更好地理解上述思想,我们来举一个通俗的例子:假设在二维平面上分布有 N 个不同的点,给定其中的某个点,现在想在平面上找到与这个点最相近的一个点,我们是怎么做的呢?首先,建立一个直角坐标系,基于该坐标系,其上的每个点就唯一地对应一个坐标 (x,y);接着引入欧氏距离;最后分别计算这个词与其他 N-1 个词之间的距离,对应最小距离值的那个词便是我们要找的词了。
二、如何生成词向量
- 基于统计方法
- 共现矩阵
2.神经网络语言模型
1、skip-gram模型
一文详解 Word2vec 之 Skip-Gram 模型(结构篇)
一文详解 Word2vec 之 Skip-Gram 模型(训练篇)
2、cbow模型
CBOW(continue bag of words)连续词袋模型:根据上下文预测中心词
先从简单的上下文只有一个词讲起(one-word context):
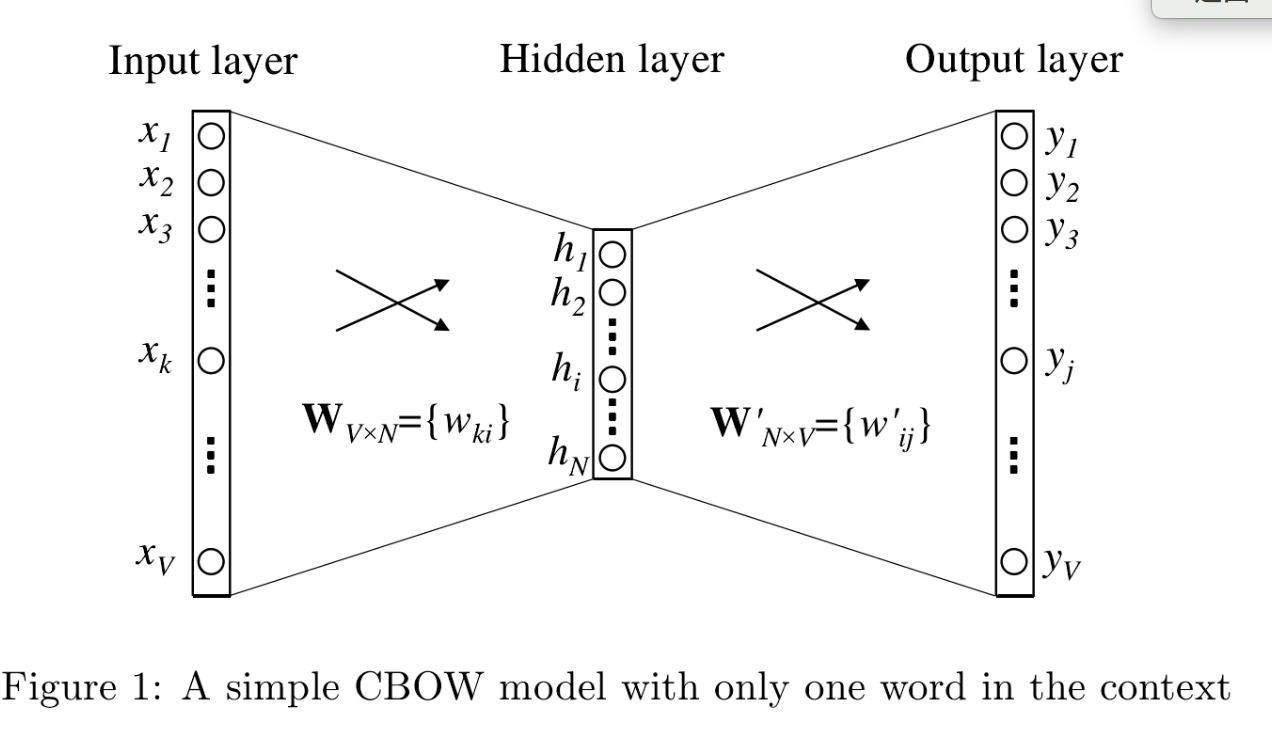
网络结构如上图所示,一共有三层:输入层,隐藏层,输出层。
参数:
输入层:一个上下文的词,用one-hot进行编码, X = (V, 1), V表示总词数,隐藏层: h = (N, 1), N表示产出词向量的维度,输入层与隐藏层之间权重矩阵 W = (V, N)
输出层 y = (V, 1),one-hot编码的形式,表示预测出的中心词,隐藏层和输出层的权重矩阵 W' = (N, V), W叫做输入矩阵,用每一行(1,N)表示表示学习到的词向量,W'叫做输出矩阵,每一列(N,1)可以表示一个词向量,一般用输入矩阵作最后的的词向量矩阵。
前馈网络:
h' = WTX + b1, h = sigmoid(h'), u = W'Th + b2, 其中uj = v'jTh, v'jT是W'中的第j列,uj表示预测是第j个词的输出值,
$\hat{y_{j}} = \frac{exp(u_{j})}{\sum_{i}^{V}exp{(u_{i})}} = \frac{exp(v_{j}^{'T}h)}{\sum_{i}^{V}exp{(v_{i}^{'T}h)}}$
损失函数:cross-entropy $CE(\boldsymbol{y},\boldsymbol{\hat{y}}) = \sum_{i}^{V}y_{i}\log \hat{y_{i}}$
参数更新:
根据损失函数, 利用梯度下降反向更新参数
主要用损失函数(CE)对 u, W', h, h', W 求导, 即$\frac{\partial CE}{\partial \boldsymbol{u}}$, $\frac{\partial CE}{\partial \boldsymbol{W^{'}}}$, $\frac{\partial CE}{\partial \boldsymbol{h}}$, $\frac{\partial CE}{\partial \boldsymbol{h^{'}}}$, $\frac{\partial CE}{\partial \boldsymbol{W}}$, $\frac{\partial CE}{\partial \boldsymbol{X}}$
(1)$\frac{\partial CE}{\partial \boldsymbol{u}}$ 损失函数对softmax进行求导,详见softmax求导
$\frac{\partial CE}{\partial \boldsymbol{u}} = \boldsymbol{\hat{y}} - \boldsymbol{y}$, 这是对网络输出向量u进行求导结果,结果也是一个V维向量,每一个元素是该位置的预测结果与真实label的差值,如果是对某一个数uj结果为:$\frac{\partial CE}{\partial u_{i}} = \hat{y}_{i} - y_{i}$,这是一个数,在$\hat{y}_{i}$表示第i个单词的预测值,$y_{i}$表示第i个单词的实际值
(2)$\frac{\partial CE}{\partial \boldsymbol{W^{'}}}$ 损失函数对第二个权重矩阵求导
我的计算应该是这样:$\frac{\partial CE}{\partial \boldsymbol{W^{'}}} = \frac{\partial CE}{\partial \boldsymbol{u}}\frac{\partial \boldsymbol{u}}{\partial \boldsymbol{W^{'}}} = (\boldsymbol{\hat{y}} - \boldsymbol{y})\boldsymbol{h}$ 但是维度不对。 $(\boldsymbol{\hat{y}} - \boldsymbol{y})$ = (V, 1), $\boldsymbol{h}$ = (N, 1)
正确结果:
$\frac{\partial CE}{\partial \boldsymbol{W^{'}}} = \frac{\partial CE}{\partial \boldsymbol{u}}\frac{\partial \boldsymbol{u}}{\partial \boldsymbol{W^{'}}} =\boldsymbol{h}(\boldsymbol{\hat{y}} - \boldsymbol{y})^{T}$, 这是标量对整个矩阵求导,结果维度为矩阵维度(N, V),
也可以写成对每个列向量$\boldsymbol{v}_{j}^{'}$进行求导,$\boldsymbol{v}_{j}^{'}$是第二个权重矩阵$\boldsymbol{W^{'}}$的第j列,因为${u}_{j}=\boldsymbol{v}_{j}^{'T}\boldsymbol{h}$,$\frac{\partial CE}{\partial \boldsymbol{\boldsymbol{v}_{j}^{'}}} = \frac{\partial CE}{\partial {u_{j}}}\frac{\partial {u_{j}}}{\partial \boldsymbol{{v}_{j}^{'}}} = \left ( \hat{y_{j}} - y_{j} \right )\mathbf{h}$
还可以写成对矩阵每个元素$\boldsymbol{W}_{ij}^{'}$进行求导: $\frac{\partial CE}{\partial {\boldsymbol{W}_{ij}^{'}}} = \frac{\partial CE}{\partial {u_{j}}} \frac{\partial u_{j}}{\partial {\boldsymbol{W}_{ij}^{'}}}=\left ( \hat{y}_{j} - y_{j} \right )h_{i}$
(3)$\frac{\partial CE}{\partial \boldsymbol{h}}$ 损失函数对隐藏层输出h求导
同上,跟我的求导方式不一致,我认为的:$\frac{\partial CE}{\partial \boldsymbol{h}} = \frac{\partial CE}{\partial \boldsymbol{u}}\frac{\partial \boldsymbol{u}}{\partial \boldsymbol{h}} =(\boldsymbol{\hat{y}} - \boldsymbol{y})\mathbf{W}^{'T}$,维度还是不对
正确结果:直接用标量对向量h求导:$\frac{\partial CE}{\partial \boldsymbol{h}} = \frac{\partial CE}{\partial \boldsymbol{u}}\frac{\partial \boldsymbol{u}}{\partial \boldsymbol{h}} =\mathbf{W}^{'}(\boldsymbol{\hat{y}} - \boldsymbol{y})$,用标量对h中每一个元素hi求导: $ \frac{\partial CE}{\partial h_{i}} = \sum_{j=1}^{V}\frac{\partial CE}{\partial u_{j}}\frac{\partial u_{j}}{\partial h_{i}} = \sum_{j=1}^{V}\left ( \hat{y}_{j} - y_{j} \right )\mathbf{W}_{ij}^{'}$
(4)$\frac{\partial CE}{\partial \boldsymbol{h^{'}}}$ 损失函数对隐藏层每加sigmoid前的向量求导
$\frac{\partial CE}{\partial \boldsymbol{h^{'}}} = \frac{\partial CE}{\partial \boldsymbol{h}}\frac{\partial \boldsymbol{h}}{\partial \boldsymbol{h^{'}}} =\mathbf{W}^{'}(\boldsymbol{\hat{y}} - \boldsymbol{y})\circ \sigma ^{'}\left ( \boldsymbol{h}^{'} \right )$
$\frac{\partial CE}{\partial h^{'}_{i}} = \frac{\partial CE}{\partial h_{i}}\frac{\partial h_{i}}{\partial h^{'}_{i}} =\sigma ^{'}\left ( h^{'}_{i} \right ) \sum_{j=1}^{V}\left ( \hat{y}_{j} - y_{j} \right )\mathbf{W}_{ij}^{'}$
(5)$\frac{\partial CE}{\partial \boldsymbol{W}}$ 损失函数对第一个权重矩阵求导
同上,顺序还是不一致
正确结果:
直接用标量对矩阵W求导 $\frac{\partial CE}{\partial \boldsymbol{W}} = \frac{\partial CE}{\partial \boldsymbol{h^{'}}}\frac{\partial \boldsymbol{h^{'}}}{\partial \boldsymbol{W}} = X\frac{\partial CE}{\partial \boldsymbol{h^{'}}}$
用标量对矩阵W中每一个元素求导:$\frac{\partial CE}{\partial {\boldsymbol{W}_{ij}}} = \frac{\partial CE}{\partial {h_{j}^{'}}} \frac{\partial h_{j}^{'}}{\partial {\boldsymbol{W}_{ij}}}=\frac{\partial CE}{\partial {h_{j}^{'}}}X_{i}$
多个上下文词
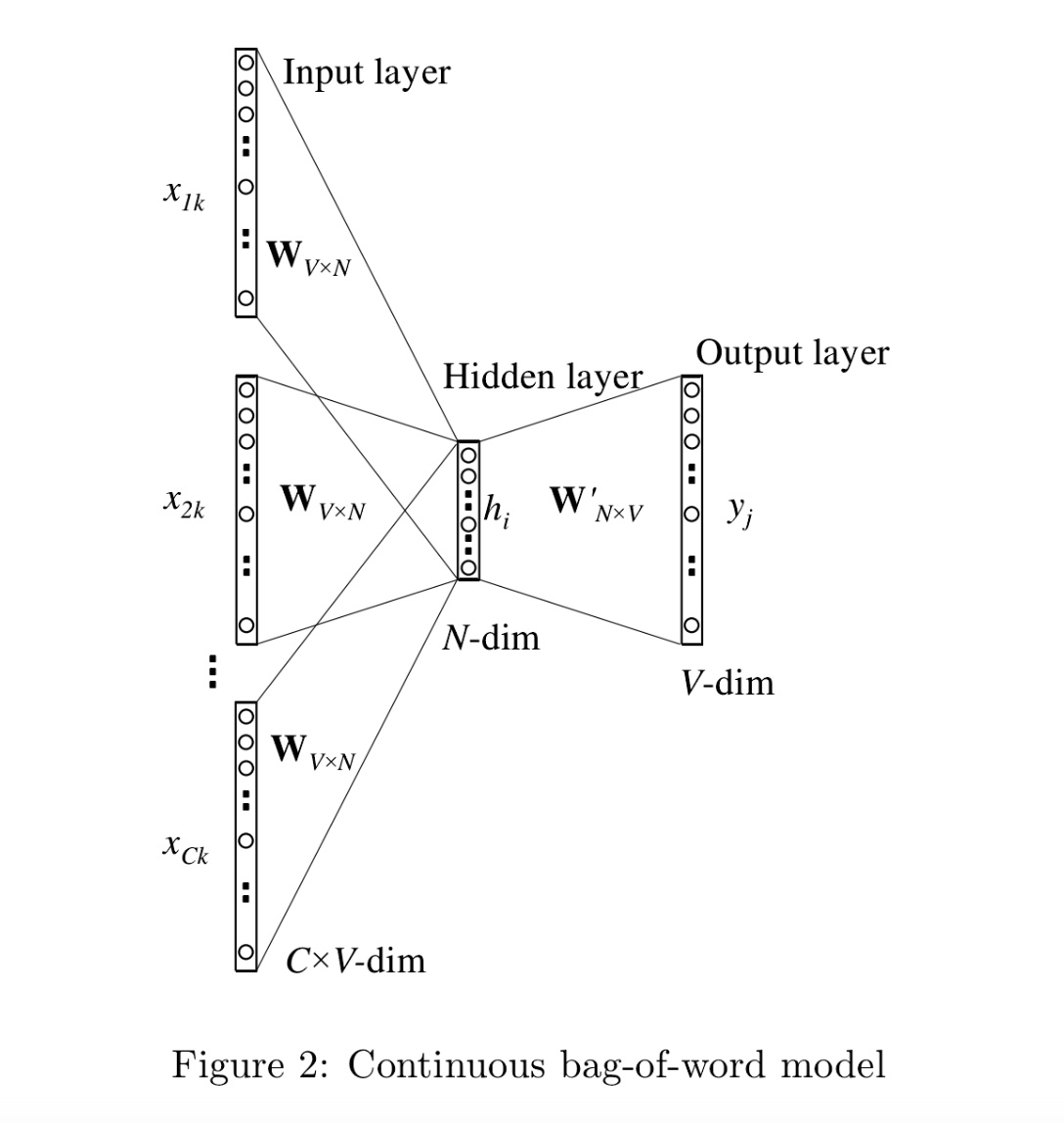
如图选取C个上下文词,CBOW模型采用取平均的方法,变成了和一个上下文词一样的形式
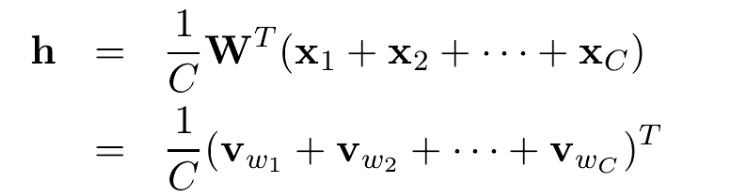
关于负采样
由$\hat{y_{j}} = \frac{exp(u_{j})}{\sum_{i}^{V}exp{(u_{i})}} = \frac{exp(v_{j}^{'T}h)}{\sum_{i}^{V}exp{(v_{i}^{'T}h)}}$知计算目标词的概率式子中分母要遍历所有的词表,非常耗费时间,所以有一种训练技巧,即随机负采样,随机采样K个不与目标词相同的词,负采样的损失函数 $J_{neg-sampling}\left ( j,\boldsymbol{h},\boldsymbol{U} \right ) = -\log \sigma \left ( v_{j}^{T}\mathbf{h} \right )-\sum_{k=1}^{K}\log \sigma \left ( -v_{k}^{T}\mathbf{h} \right ) $ ,其中$ \sigma\left ( -x \right ) = 1 - \sigma \left (x \right ) $, 解释不了具体的意思,感觉很对,为什么要用sigmoid, 除以负采样的意义是什么?
负采样求导,主要是 $\frac{\partial J}{\partial v_{j}^{T}}, \frac{\partial J}{\partial\boldsymbol{ h}}, \frac{\partial J}{\partial v_{k}^{T}}, $
$\frac{\partial J}{\partial \mathbf{h}} = \left ( \sigma -1 \right )v_{j} + \sum_{k=1}^{K}(1-\sigma)v_{k}$
$\frac{\partial J}{\partial v_{j}} = \left ( \sigma -1 \right )\boldsymbol{h}$
$ \frac{\partial J}{\partial v_{k}} = -\left (\sigma \left ( -v_{k}^{T}\mathbf{h} \right ) - 1 \right )\boldsymbol{h}$
关于hierarchical softmax
构造一个V个叶节点的哈夫曼树,每个叶节点都是一个词表的单词,从root到叶节点的路径,就等于这个节点的概率,原来softmax的时间复杂的是O(n),现在是lg(n)
3、skip-gram与cbow的对比
cbow是以周围词作为输入,中心词作为目标的网络,所以假设一篇语料中有V个单词,那么cbow将会以每一个单词作为中心词进行训练,因此会有V次
skip-gram是以中心词作为输入,周围词作为目标的网络,那么对于一篇语料来说,每一个词都会作为中心词,每个中心词周围大小选择K个,那么将会进行KV次
直观上来看,cbow训练次数要比skip-gram少,也即精确率不如skip-gram,但是效率高,速度快。
遇到生僻词,cbow效果会大大降低
3.GLOVE模型



