【深度学习】RNN | GRU | LSTM
目录：
1、RNN
2、GRU
3、LSTM
一、RNN
1、RNN结构图如下所示：
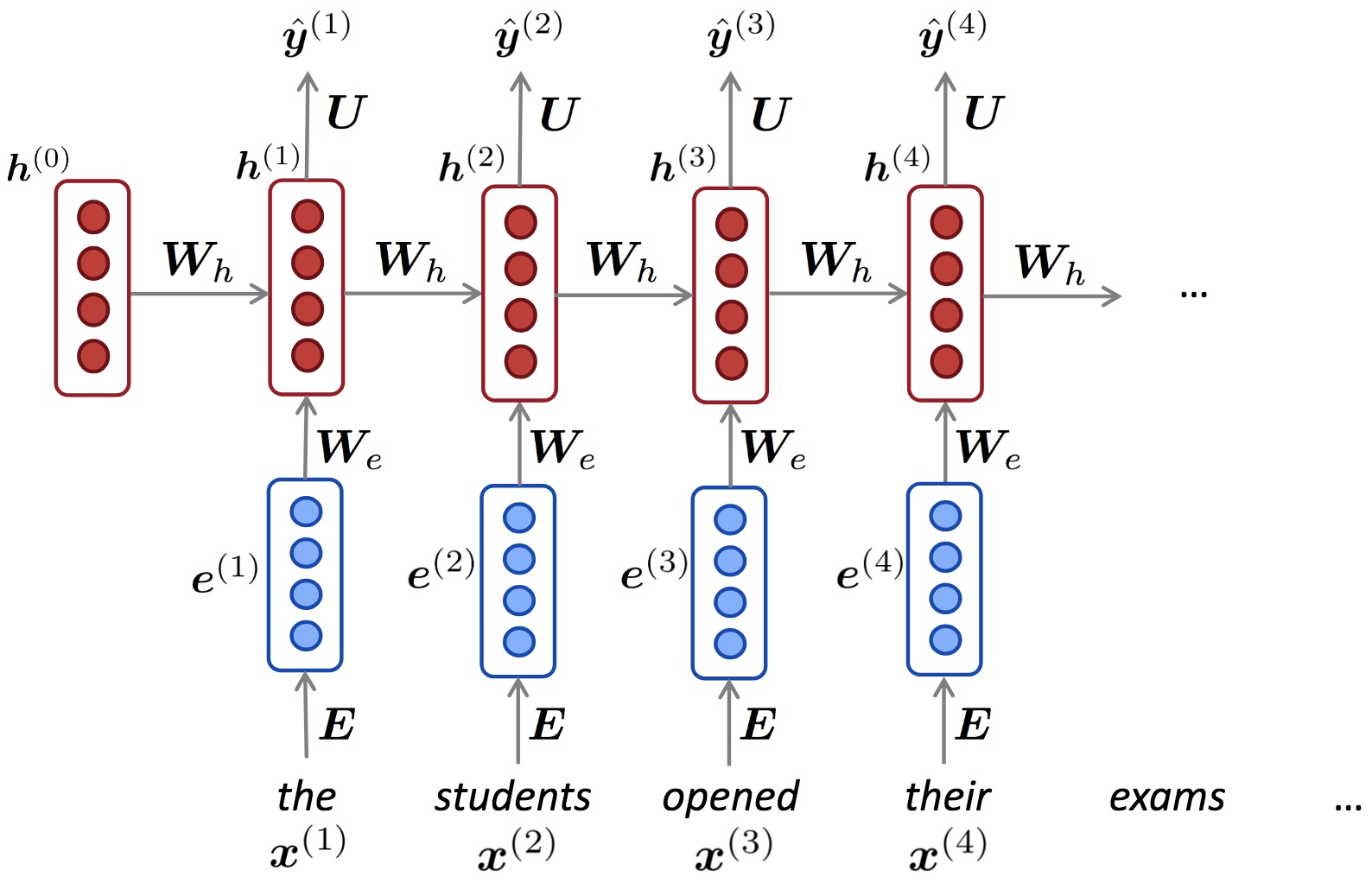
其中：
$a^{(t)} = \boldsymbol{W}h^{t-1} + \boldsymbol{W}_{e}x^{t} + \mathbf{b}$
$h^{t} = f(a^{t})$, f 是激励函数，sigmoid或者tanh
$\hat{y}^{t} = Uh^{t}$
2、RNN中的梯度消失与梯度膨胀
总损失是所有时间步的和：$E = \sum_{t=1}^{T}E_{t}$，所以$\frac{\partial E}{\partial W} = \sum_{t=1}^{T}\frac{\partial E_{t}}{\partial W}$
而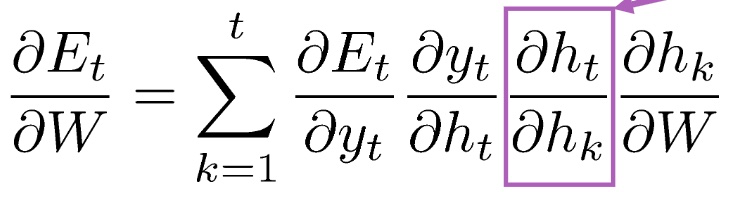
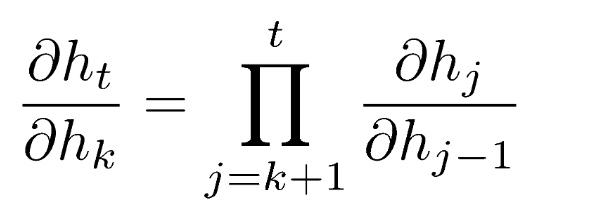
$\frac{\partial h_{j}}{\partial h_{j-1}} = \frac{\partial f(a_{j})}{\partial h_{j-1}} = f^{'}(a_{j})W$, 不知道是W还是WT，大概是这样的，因为是累乘，所以如果f'太大或者太小就会梯度膨胀或消失
二、GRU
参考 https://towardsdatascience.com/understanding-gru-networks-2ef37df6c9be
相对于RNN来说，GRU主要增加了两个门 重置门 r 和 更新门 u，重置门用来决定会保留多少历史信息，如果是0的话，就不会保持历史信息；更新门用来衡量当前与历史的取舍
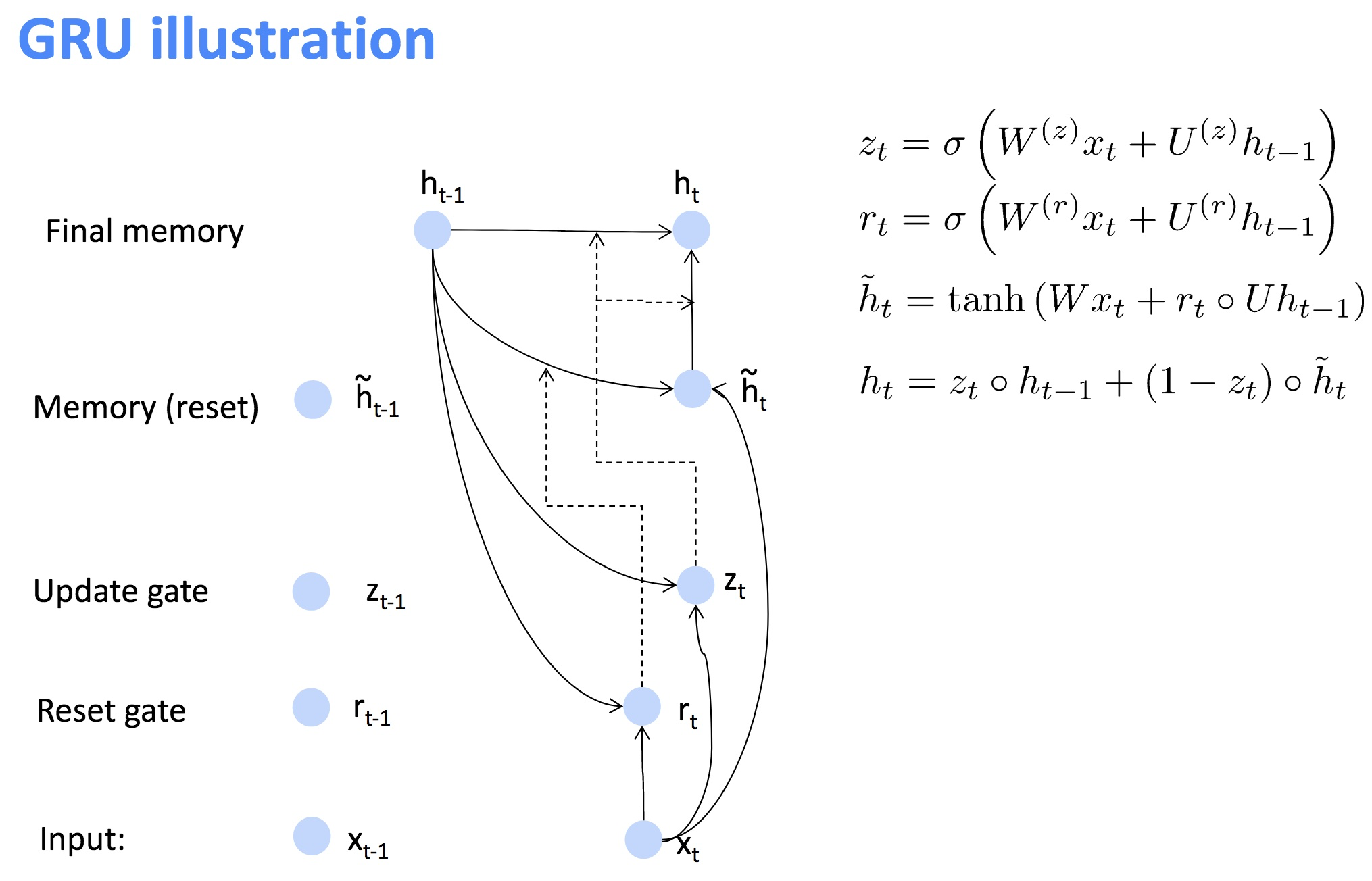
GRU是如何解决梯度消失与膨胀的？https://www.cs.toronto.edu/~guerzhoy/321/lec/W09/rnn_gated.pdf
好像是这样，但是感觉还是不能解决梯度消失，如果zj和后面的偏导都非常小，还是会梯度弥散？
三、LSTM
