矩阵向量求导术
在标量、向量和矩阵的求导过程中一定要知道最后结果的形状。
这里总结几个常见的求导形式:
前言:
最基础最重要的,标量对向量求导和向量对标量求导,有两种方式,分子布局和分母布局,不同的方式都是对的,只是结果缺一个转置
1、矩阵乘以列向量,对列向量求导,形如 $\boldsymbol{z} = \boldsymbol{Wx},$, 求$\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{x}}$
假设$\boldsymbol{W}\in \mathbb{R}^{n\times m},\boldsymbol{x}\in \mathbb{R}^{m\times 1}$, 则$\boldsymbol{z}\in \mathbb{R}^{n\times 1}$, 所以$\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{x}}$ 是n维向量对m维向量求导,最后是一个(n x m)的雅可比矩阵
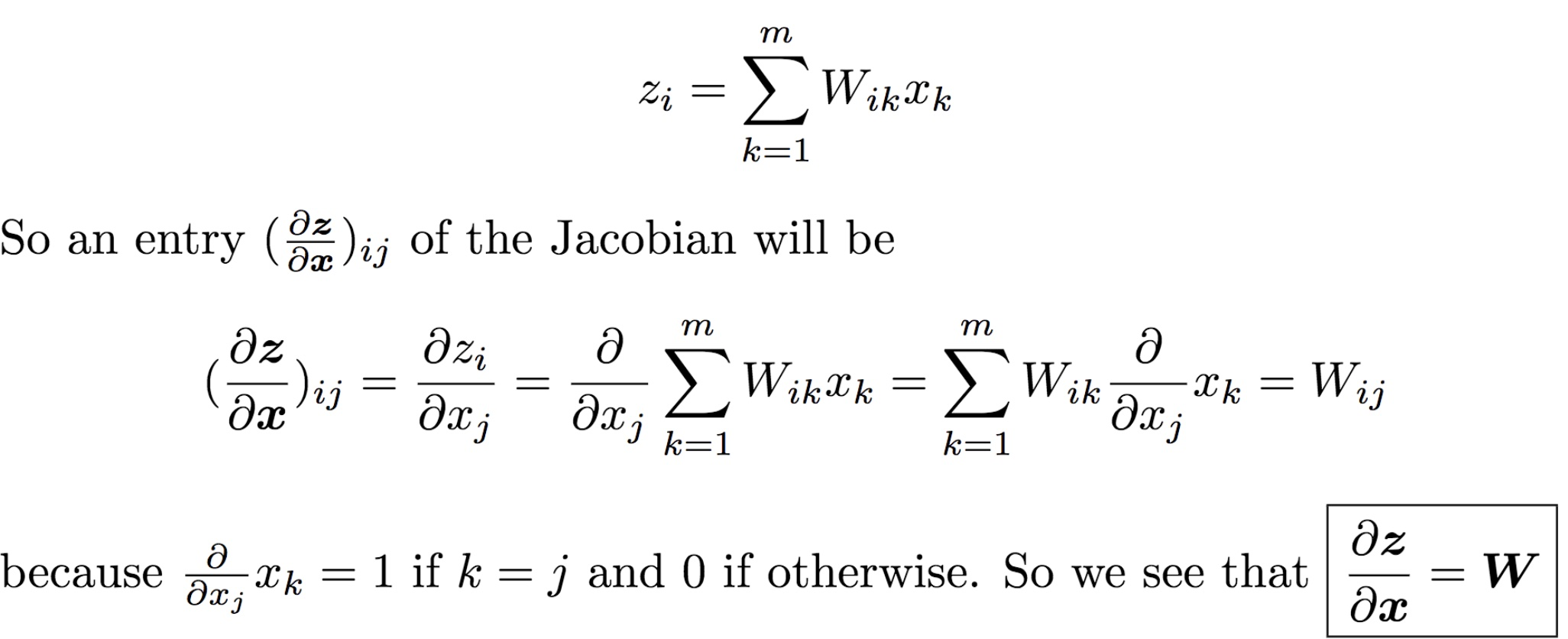
2、行向量乘以矩阵,对行向量求导,形如$\boldsymbol{z} = \boldsymbol{xW}, $, 其中$ \boldsymbol{W}\in \mathbb{R}^{n\times m} \boldsymbol{x}\in \mathbb{R}^{1\times n} $则$\boldsymbol{z}\in \mathbb{R}^{1\times m}$,所以$\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{x}}$是m维行向量对n维行向量求导,结果是(m, n)维矩阵
z向量每一个元素求解如下:$z_{i}= \sum_{k=1}^{n}x_{k}W_{ki}$,
$\left (\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{x}} \right )_{ij} = \frac{\partial z_{i}}{\partial x_{j}} = \sum_{k=1}^{n}W_{ki}\frac{\partial x_{k}}{\partial x_{j}} = W_{ji}$,所以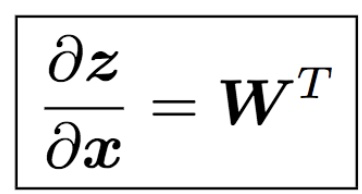
3、一个向量对自己求导
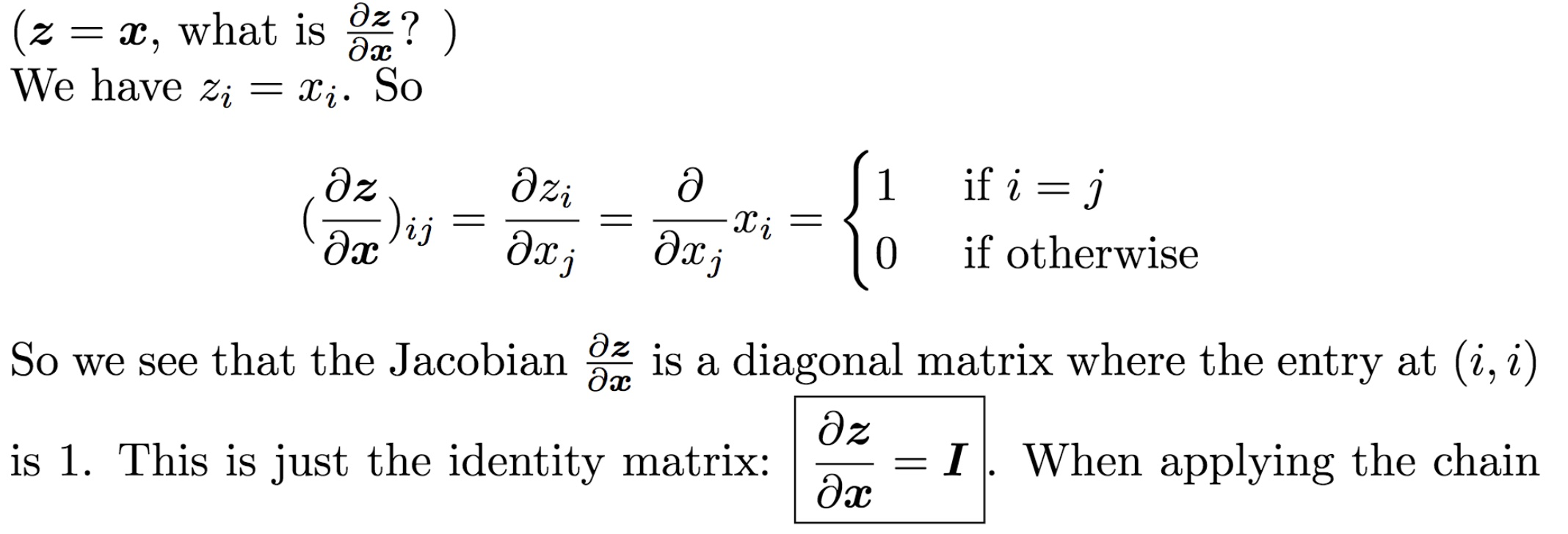
4、对向量每一个元素都施加的函数,对向量求导

如果 $\boldsymbol{x}\in\mathbb{R}^{1\times n},$, 则$\boldsymbol{z}\in\mathbb{R}^{1\times n},$, $\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{x}}$是(n x n)的对角矩阵,对角元素为$\frac{\partial \boldsymbol{z}_{i}}{\partial \boldsymbol{x}_{i}}$, 乘以一个对角矩阵可以写成分别与每一个元素相乘,即$\circ f^{'}\left ( x \right )$
5、矩阵乘以列向量,最后的标量对矩阵求导
![]()
假设$\boldsymbol{W}\in \mathbb{R}^{n\times m},\boldsymbol{x}\in\mathbb{R}^{m\times 1}$, 则$\boldsymbol{z}\in \mathbb{R}^{n\times 1}$ 是一个 (n x 1)的向量对 (n x m)的向量求导,结果是 n * n * m维,为了避免求解这么复杂的,可以计算$\frac{\partial \mathbf{z}}{\partial W_{ij}}$
$ \mathbf{z}_{k}= \sum_{l = 1}^{m}W_{kl}x_{l}$
$\frac{\partial \mathbf{z}_{k}}{\partial W_{ij}} =\frac{\partial \sum_{l = 1}^{m}W_{kl}x_{l}}{\partial W_{ij}} = \sum_{l=1}^{m}x_{l}\frac{\partial W_{kl}}{\partial W_{ij}}$ 当且仅当 k == i && l == j时,导数结果为 xj,当 k != i时,结果为0

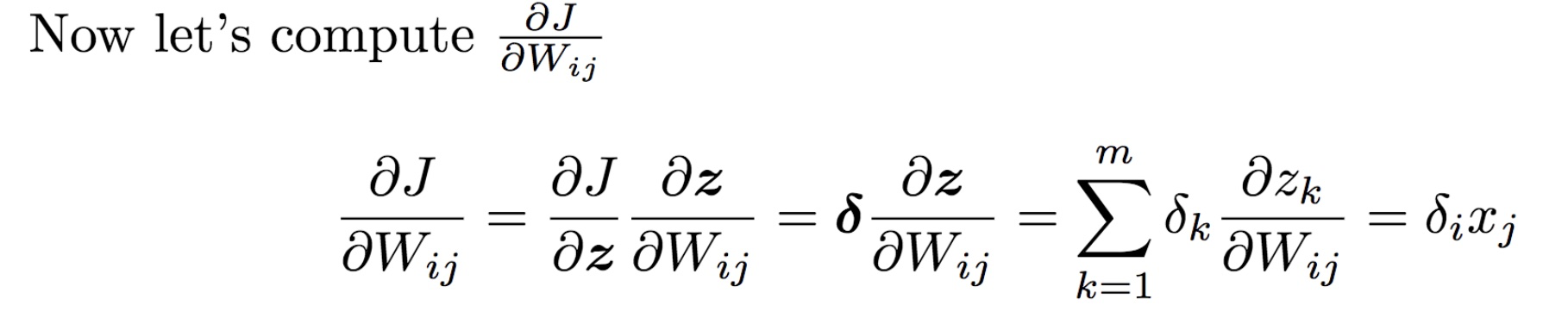
这里使用的是分子布局,所以
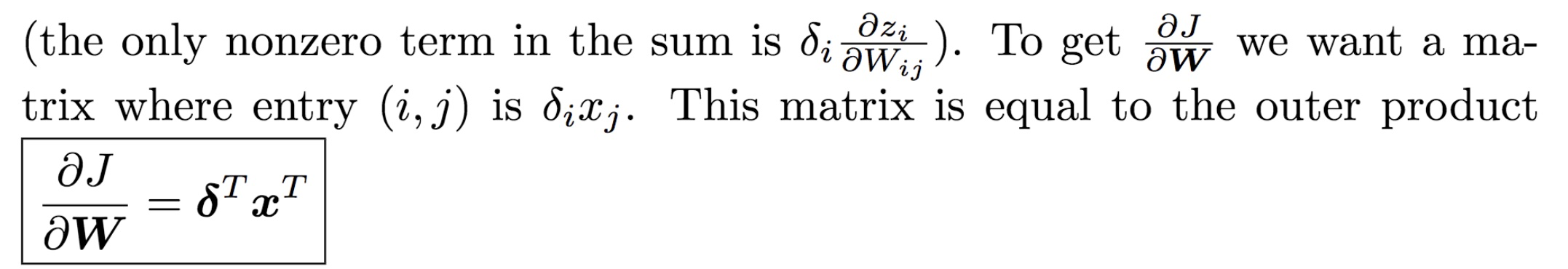
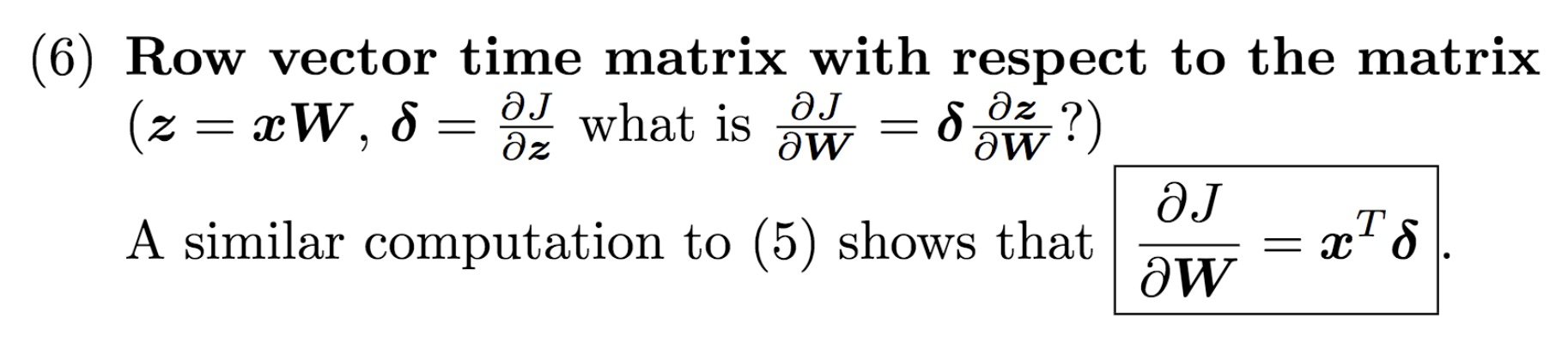
(7) $\frac{\partial \boldsymbol{Wx}}{\partial \boldsymbol{x}}$
参考:
https://web.stanford.edu/class/cs224n/readings/gradient-notes.pdf




