深度学习练习(一)

(一)画出三点图实例(polt.py)

import matplotlib.pyplot as plt　　　　　　　　　　　　　　　　#导入matplotlib模块里面的pyplot类，并取一个别名为plt

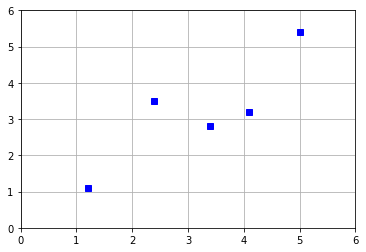
dataset = [[1.2, 1.1], [2.4, 3.5], [4.1, 3.2], [3.4, 2.8], [5, 5.4]]　　 #创建矩阵数据并赋值为dataset

x = [row[0] for row in dataset]　　　　　　　　　　　　　　　　#循环dataset里面第一列并赋值为x

y = [row[1] for row in dataset]　　　　　　　　　　　　　　　　#循环dataset里面第二列并赋值为y

plt.axis([0, 6, 0, 6])　　　　　　　　　　　　　　　　　　　　　#通过plt里面的axis函数画一个6-6的图

plt.plot(x, y, 'bs')　　　　　　　　　　　　　　　　　　　　　　#以x轴和y轴的序列为坐标绘制图，bs表示格式为蓝色方块,bo表示蓝色圆点,b-蓝色的线条-,g^表示的是绿色三角形

plt.grid()　　　　　　　　　　　　　　　　　　　　　　　　　#grid方法表示显示网格线

plt.show()　　　　　　　　　　　　　　　　　　　　　　　　　　#show()用于在屏幕上显示前面绘制的图片

plt.savefig('scatter.png')　　　　　　　　　　　　　　　　　　　　#保存的图片名称

(二)计算回归系数

dataset = [[1.2, 1.1], [2.4, 3.5], [4.1, 3.2], [3.4, 2.8], [5, 5.4]]
x = [row[0] for row in dataset]
y = [row[1] for row in dataset]

def mean(values):
return sum(values) / float(len(values))

def covariance(x, mean_x,mean_y):
covar = 0.0
for i in range(len(x)):
covar += (x[i] - mean_x) * (y[i] - mean_y)
return covar

def variance(values, mean):
return sum([(x-mean) **2 for x in values])

def coefficients(dataset):
x_mean, y_mean = mean(x), mean(y)
w1 = covariance(x, x_mean, y_mean) / variance(x, x_mean)
w0 = y_mean - w1 * x_mean
return w0, w1

w0, w1 = coefficients(dataset)
print('回归系数分别为: w0=%.3f, w1=%.3f' % (w0, w1))

(三)实现标准简单线性回归

from math import sqrt
dataset = [[1.2, 1.1], [2.4, 3.5], [4.1, 3.2], [3.4, 2.8], [5, 5.4]]

def mean(values):
return sum(values) / float(len(values))

def covariance(x, mean_x, y, mean_y):
covar = 0.0
for i in range(len(x)):
covar += (x[i] - mean_x) * (y[i] - mean_y)
return covar

def variance(values, mean):
return sum([(x-mean) ** 2 for x in values])

def coefficients(dataset):
x = [row[0] for row in dataset]
y = [row[1] for row in dataset]
x_mean, y_mean = mean(x), mean(y)
w1 = covariance(x, x_mean, y, y_mean) / variance(x, x_mean)
w0 = y_mean - w1 * x_mean
return (w0, w1)

def rmse_metric(actual, predicted):
sum_error = 0.0
for i in range(len(actual)):
prediction_error = predicted[i] - actual[i]
sum_error += (prediction_error ** 2)
mean_error = sum_error / float(len(actual))
return sqrt(mean_error)

def simple_linear_regression(train, test):
predictions = list()
w0, w1 = coefficients(train)
for row in test:
y_model = w1 * row[0] + w0
predictions.append(y_model)
return predictions

def evaluate_algorithm(dataset, algorithm):
test_set = list()
for row in dataset:
row_copy = list(row)
row_copy[-1] = None
test_set.append(row_copy)
predicted = algorithm(dataset, test_set)
for val in predicted:
print('%.3f\t' %(val))

actual = [row[-1] for row in dataset]
rmse = rmse_metric(actual, predicted)
return rmse

rmse = evaluate_algorithm(dataset, simple_linear_regression)
print('RMSE: %.3f' % (rmse))

 (四)生成山鸢尾可视化图

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header = None)
X=df.iloc[0:150,[0,2]].values
plt.scatter(X[0:50,0],X[:50,1],color='blue',marker='x',label='setosa')
plt.scatter(X[50:100,0],X[50:100,1],color='red',marker='o',label='versicolor')
plt.scatter(X[100:150,0],X[100:150,1],color='green',marker='*',label='virginica')
plt.xlabel('petal width')
plt.ylabel('sepal length')
plt.legend(loc='upper left')
plt.show()