数据结构1——聊聊树状数组的那些事

数据结构1——聊聊树状数组的那些事

目录

Part1.那些树状数组能解决的问题

Part2.lowbit

Part3.初识树状数组

Part4.树状数组的性质

Part5.树状数组与区间查询

Part6.树状数组与单点修改

Part7.树状数组与建树

Part8.树状数组与逆序对

Part9.权值树状数组与动态第k小

Part01:那些树状数组能解决的问题

树状数组能解决区间修改单点查询，单点修改区间查询，动态第 \(k\) 小的数，逆序对等问题。

有时，在差分数组和辅助数组的帮助下，树状数组还可解决更强的区间加单点值和区间加区间和问题。

树状数组可以解决的问题，线段树也一定能解决。但是线段树能解决的问题，树状数组不一定能解决。

但是，线段树和树状数组能共同解决的问题中，树状数组的效率更高，且码量更小，可以节约一点比赛时的时间和评测所用的时间。

所以，树状数组也具有一定的价值，值得我们学习。

（线段树是数据结构2的内容）

Part02:lowbit

在很久以前我们学习过二进制。我们知道，\(\text{lowbit}(x)\)，表示一个数的二进制从后往前数第一个 \(1\) 及其右边的 \(0\) 所构成的二进制的数（如 \((1000000000)_2\)）所代表的十进制值。

那 \(\text{lowbit}\) 怎么简便求出呢？

设一个二进制数 \(x\) 的最低位 \(1\) 是第 \(k\) 位，则它的 \(0\to k-1\) 位都是 \(0\)。

那么此时，\(-x\)，即 \(\text{~}x+1\)，也即 \(x\) 取反再 \(+1\)，会把 \(k+1\) 到最高位全部取反，但因为 \(0\to k-1\) 位都是 \(0\)，取反后均变为 \(1\)，然后由于 \(+1\)，又全部变为 \(0\)，进位到第 \(k\) 位，而第 \(k\) 位又取反变为 \(0\)，加上进位 \(1\) 正好又变为 \(1\)，与原来的数一做与运算，就可以把 \(k+1\) 位到最高位全部消掉，就剩下 \(0\to k\) 位，也即 \(\text{lowbit(x)}\) 了。

所以 \(\text{lowbit(x)}=x\text{&}-x\)。

实现：

int lowbit(int a)
{
	return a&(-a);
}

Part03:初识树状数组

在很久以前，我们曾学习过前缀和。它能让我们快速得到一个区间的和。但是预处理它太慢了，而且一旦是动态数组，那前缀和的效率就会锐减。这时，树状数组登场了。

我们可以假设，我们需要求 \(a_1\) 到 \(a_7\) 的和。用前缀和的话，我们只能用 \(a_1+a_2+a_3+a_4+a_5+a_6+a_7\)。但是，如果有三个变量 \(A=a_1+a_2+a_3+a_4,B=a_5+a_6,C=a_7\)，那么， \(a_1\) 到 \(a_7\) 的和就变成了 \(A+B+C\)，十分方便。

我们将一段前缀拆成不多于 \(\log n\) 个的区间，那么这 \(\log n\) 段区间的信息（和、积等）就变成了已知的。

那如何求这 \(\log n\) 个区间呢？

如下图，这就是一个树状数组。

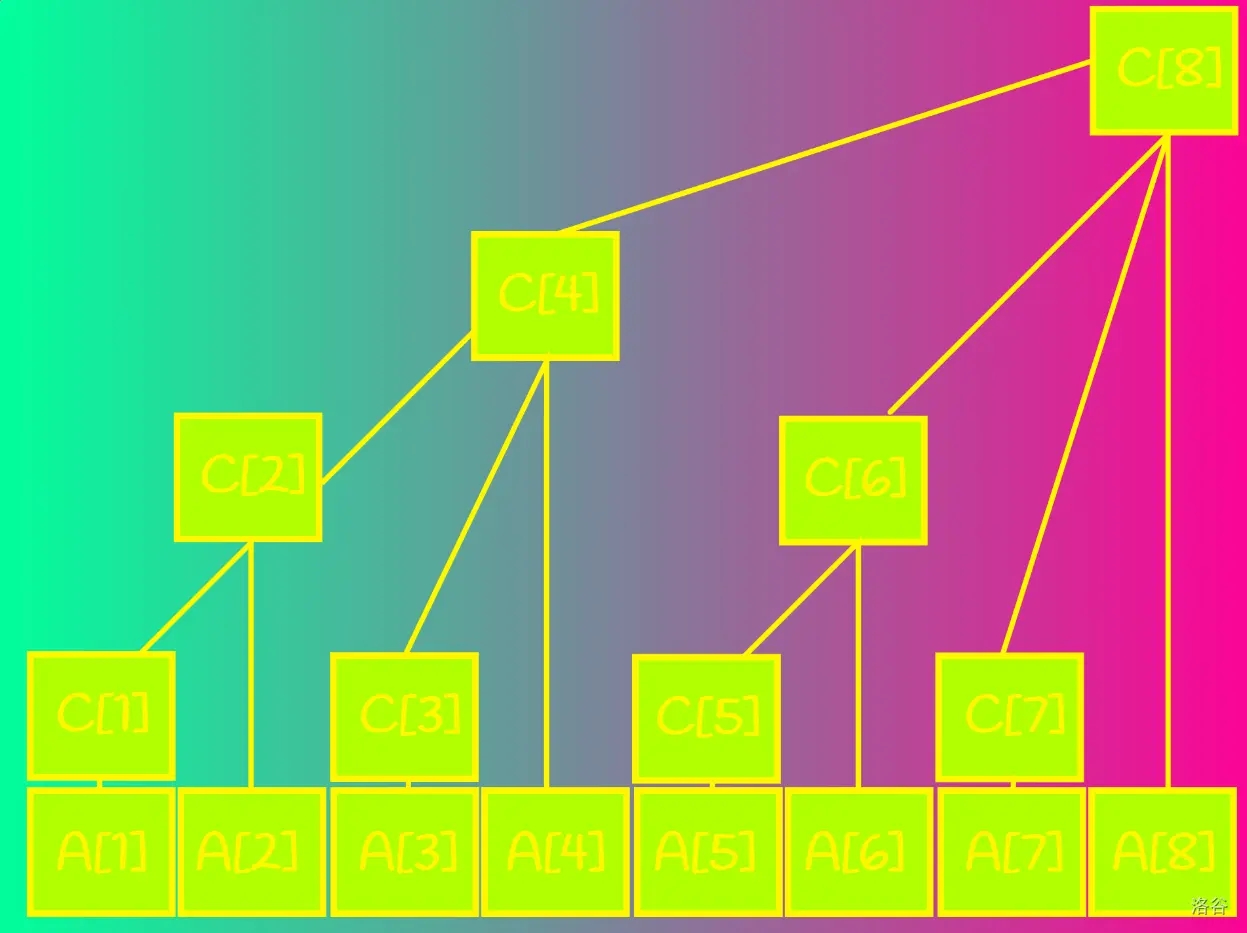
我们可以发现，在这个树状数组中，\(c_1\) 管辖的是 \(a_1\)，\(c_2\) 管辖的是 \(c_1\) 和 \(c_2\)，\(c_3\) 管辖的是 \(a_3\)，\(c_4\) 管辖的是 \(c_2,c_3\) 和 \(a_4\)…

这时，当我们想要计算 \(a_1\) 到 \(a_7\) 的和，可以按照如下步骤：

先看 \(c_7\)，发现 \(c_7\) 管辖 \(a_7\)，然后看 \(c_{7-1=6}\)，发现 \(c_6\) 管辖 \(a_5,a_6\)，然后看 \(c_{5-1=4}\)，发现 \(c_4\) 管辖 \(a_1,a_2,a_3,a_4\)，然后看 \(c_{1-1=0}\)，发现 \(c_0\) 不存在，步骤结束。

我们看的三个数 \(c_7,c_6,c_4\) 加起来就是 \(a_1\) 到 \(a_7\) 的和。

Part04:树状数组的性质

树状数组具有如下性质：

1.每一个 \(c\) 数组的元素都管辖了以它为根的子树里的与元素之和。

2.每个节点的父亲节点都是（设下标为 \(x\) 且除根结点） \(x+\text{lowbit(x)}\)。

3.\(\text{lowbit(x)}\) 即为以 \(x\) 为根的子树的叶子结点个数。

Part05:树状数组与区间查询

根据树状数组的性质 \(3\)，设我们要查 \(a_1\) 到 \(a_x\) 的和，可以不断地先把答案加上 \(c_x\)，再将 \(x-\text{lowbit}(x)\) 直到 \(x=0\) 来得到答案。

实现：

int ret(int x)
{
	int ans=0;
	while(x>0)
	{
		ans+=c[x];
		x-=lowbit(x);
	}
	return ans;
}

Part06:树状数组与单点修改

需要用到树状数组的题，一般都是动态的，这时我们就需要修改。

根据树状数组的性质 \(2\)，当我们将一个数（设其下标为 \(x\)）加上 \(y\) 时，我们需要把 \(c_x\) 的父亲节点都加上 \(y\)，这就是单点修改。

实现：

void add(int x,int y)
{
	while(x<=n)
	{
		c[x]+=y;
		x+=lowbit(x);
	}
}

减 \(y\) 乘 \(y\) 除 \(y\) 等都能解决，万能法宝。

Part07:树状数组与建树

初学树状数组，我们可以用时间复杂度 \(O(n\log n)\) 的建树算法。

建树，其实可以转化为 \(n\) 次单点修改。

即对于一个下标为 \(i\) 的数 \(a_i\)，使用单点修改的 \(\text{add}\) 函数，\(\text{add}(i,a_i)\) 就能建树了。

实现：

void build(int l,int r)
{
	for(int i=l;i<=r;i++)
	{
		add(i,a[i]);
	}
}

Part08:树状数组与逆序对

逆序对怎么用树状数组求呢？

可以对于 \(1\) 到 \(n\)，求出 \(1\to a_i\) 的和，用答案加上这个值后，单点修改 \(i\)（加上 \(a_i\)）。

Part09:权值树状数组与动态第k小

权值线段树（数据结构2内容）有了，怎么能没有权值树状数组呢？

它们一般都是用来解决第k小的问题的。

那么怎么做呢？

考虑倍增（提高组算法详解7内容）。

设 \(x=0\)，\(sum=0\)，枚举 \(i\) 从 \(\log_2n\) 降为 \(0\)：

• 查询权值数组中 \(x+1\to x+2^i\) 的区间和 \(t\)。
• 如果 \(sum+t<k\)，扩展成功，\(x=x+2^i\)，\(sum=sum+t\)；否则扩展失败，不操作。

这样得到的 \(x\) 满足 \(1\to x\) 前缀和 \(<k\) 的最大值，所以最终 \(x+1\) 就是答案。

当然也可以用并查集来解决。

代码：

int slove(int k)
{
	int sum=0,x=0;
	for(int i=log2(n);i>=0;--i)
	{
		x+=1<<i;
		if(x>= n||sum+t[x]>=k)
		{
			x-=1<<i;
		}
		else
		{
			sum+=t[x];
		}
	}
	return x+1;
}

至此，数据结构1就结束了。