Math4ML 优化与加速

共12章：基础概论、凸优化与无约束优化、最速下降法、牛顿法及其改进、共轭梯度法、拟牛顿法、约束优化、对偶定理、ML的风险与损失、梯度法及其改进、动量法及其改进、带约束的优化算法。

无约束优化——1 最速下降法

无约束优化——2 牛顿法

无约束优化——3 共轭梯度法

 最速下降法和共轭梯度法的区别在于，共轭梯度法多了一个修正方向的步骤，仅此而已，例题：

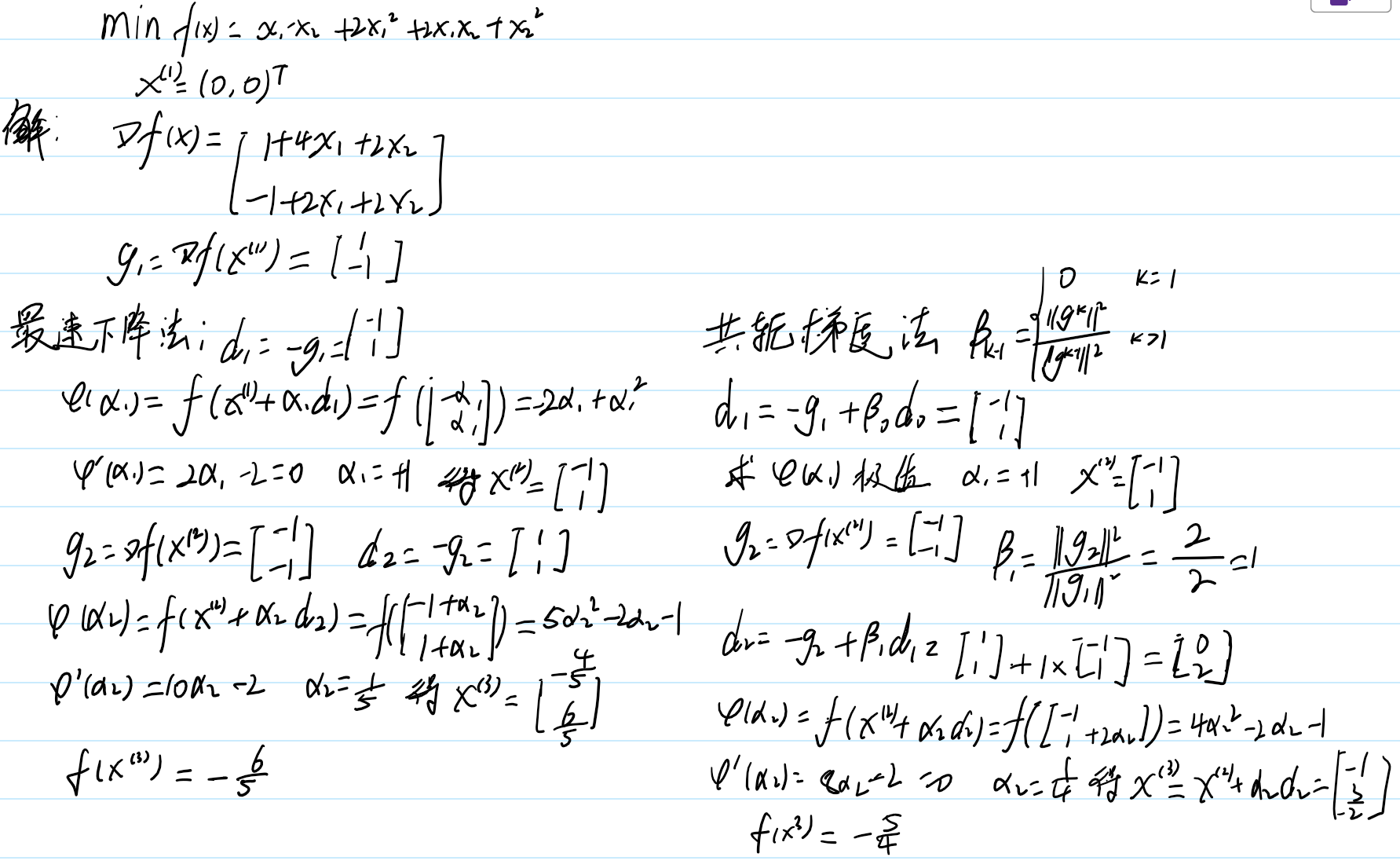
可以对比感受其中差异。

无约束优化——4 拟牛顿法

牛顿法和拟牛顿法区别在于DFP法用自适应的简单的矩阵去代替二阶导逆矩阵，并且每次迭代中多了一个迭代该矩阵的步骤，仅此而已，

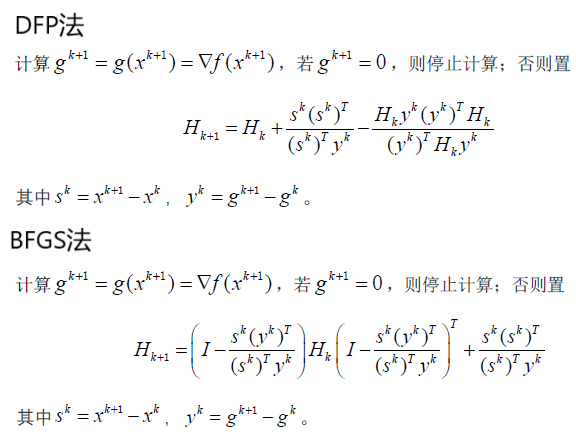
例题：

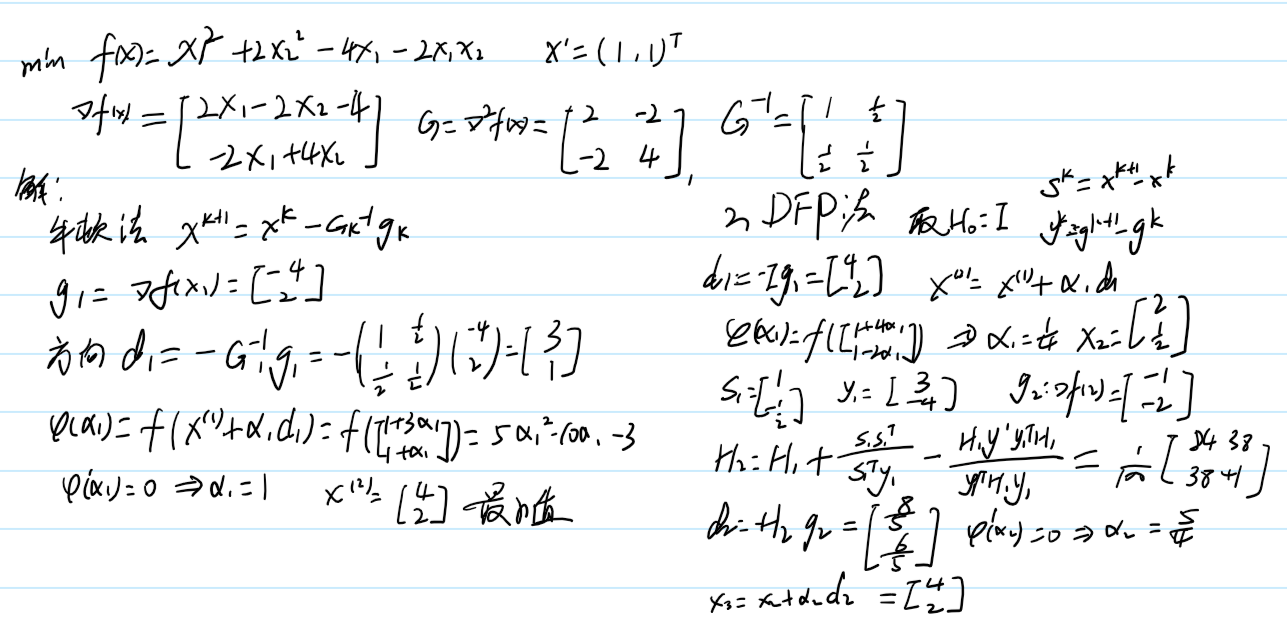
感受其中差异。

约束优化

很容易写出一个优化模型的KKT条件，只需要

1 写出拉格朗日函数，求梯度。

2 原始约束，包括等式和非等式

3 关于不等式约束，(1) 乘子大于等于0; (2)乘子和不等式左项 整体等于0。

以上三个组合起来，加上变量满足的取值范围，就是所有KKT条件了。

求解方法，很简单，分2类讨论，不等式约束的乘子为0的情况，然后不为0的情况，解方程求解。

例题：分类讨论λ为0的时候，我算过了，无解，过程略；所以λ不为0，那么不等式约束直接取等号，过程如下：

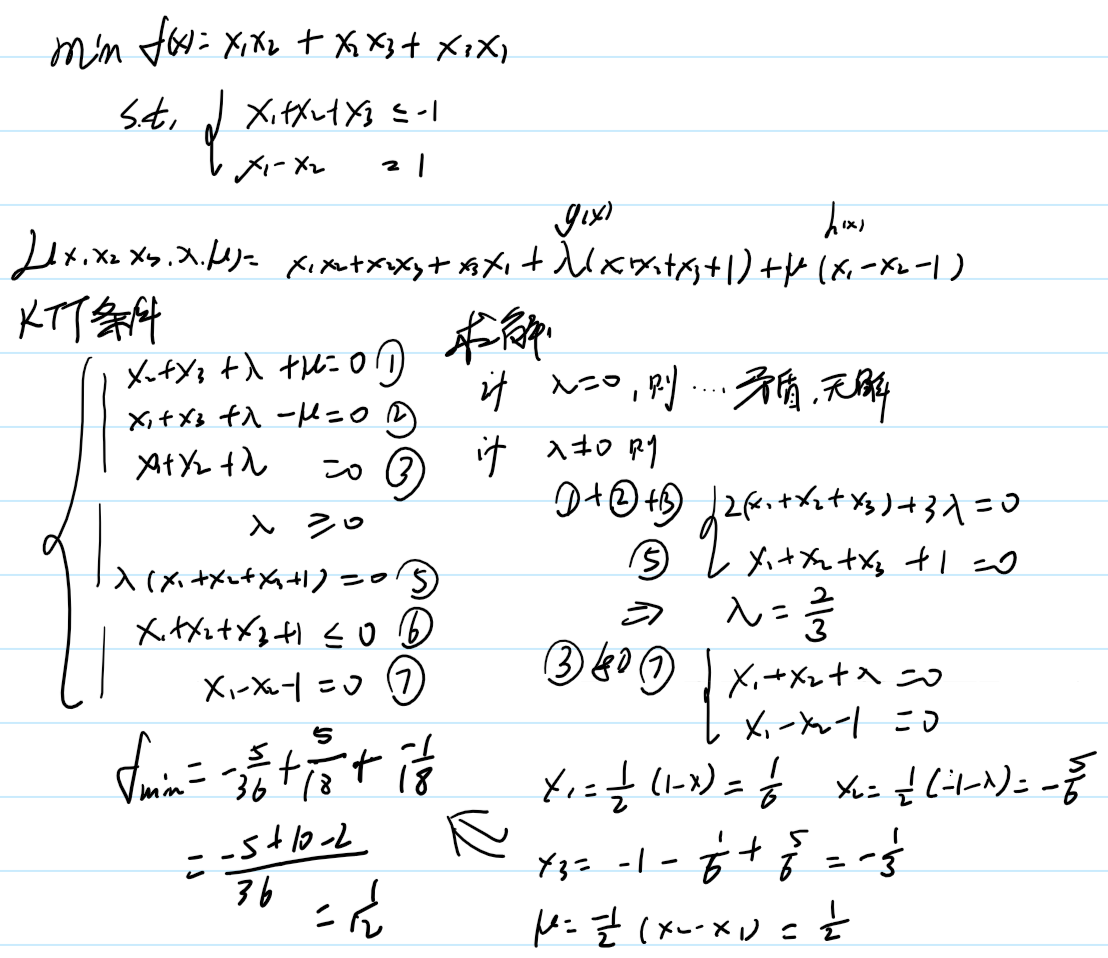
 end

约束优化-对偶理论

方法和例题：

容易迷糊的点在于 等式与无约束的情况，注意即可。

梯度法及其改进

GD

AGD(加速梯度法)

SGD

SAG（Stochastic Average Gradient）、SAGA、SVRG

动量法及其改进

Momentum动量法

Nesterov加速算法

AdaGrad

RMSProp(Root Mean Square PRopogation)

Adam

基础知识：导数和极值的理论，重点是 偏导数、鞍点、梯度等等。

凸优化基本概念：常见凸集：射线、超平面、半空间等。凸锥、极方向、凸集分离定理、凸函数。

最优化基本概念：

常见优化问题：线性与非线性规划、二次规划、锥优化、整数规划、动态规划。

无约束优化问题的最优性条件：

-一阶必要条件：局部极小点处梯度为0.

-二阶必要条件：局部极小点处梯度为0，且二阶导半正定。

-二阶充分条件：梯度为0，且二阶导正定的点为局部极小点。

步长搜索：

-精确一维线搜索

-非精确线搜索准则：Armijo准则（Goldstein准则、Wolfe准则）、黄金分割法。