ML-集成学习、特征选择与稀疏学习
集成学习根据个体学习器的生成方式分为Bagging和Boosting两大类。
Bagging的个体学习器之间不存在强依赖关系,Boosting存在强依赖关系。
Bagging可以同时生成的并行化方法,Boosting必须串行化生成的序列化方法。
Bagging
Bootstrap aggregating,即使用自主采样法来构造基学习器。
Bagging有两个要求:1 多样性要求指个体学习器应尽可能独立;2 准确性要求指个体学习器不能太差。
自主采样法的特点是,每个样本有0.368的概率无法被采样到,这部分剩余样本可以用于验证集的包外估计,例如决策树的剪枝、神经网络的early stop。
Bagging的训练复杂度与训练基学习器的复杂度同阶。Bagging可以直接用于多分类、回归等任务。
Bagging要求基学习器在数据集上较小的扰动可以使分类结果产生显著的变动,如此得到的基分类器之间的差异性较大。
Bagging的案例有:Random Forest 随机森林,以决策树为基学习器。RF的训练效率比Bagging更好,它们的基学习器都是决策树,在训练时会在当前节点的属性集合中选择最优属性。区别就在于此:普通的决策树Bagging集成学习在选择决策树分支划分属性时,会在当前节点的属性集合中选择一个最优属性,而且要考察结点的所有属性;而随机森林对于基决策树的每个节点,先从该节点的属性集合考察一个属性子集,然后从该子集中选择一个最优属性用于划分。
Boosting
什么是强可学习与弱可学习?强可学习是指一个概念存在一个多项式的学习算法可以学习并且正确率很高;弱可学习指一个概念存在一个多项式学习算法能够学习但是正确率仅比随机猜测略好。Boosting方法就是一族可以把弱学习器提升为强学习器的算法。
Boosting的基本思想是:迭代过程中尝试纠正先前模型所产生的错误,迭代次数越多集成产生的错误就越少,至少在数据支持的范围内和过拟合之前。
个体学习器之间存在强依赖关系,并且每个个体学习器都需要串行生成,然后使用组合策略得到最终的集成模型,然后就是boosting。
Boosting的案例有:
AdaBoost:是一个加法模型,损失函数为指数函数(对一般的损失函数不适用),学习算法为前向分步算法,是一个二分类学习方法。
AdaBoost每一个步骤的新模型都是基于前一个模型的表现结果进行调整的。AdaBoost 本质就是,每次迭代更新样本分布,然后对新的分布下的样本学习一个弱分类器,和它对应的权重。更新样本分布的规则是:减小之前弱分类器分类效果较好的数据的概率,增大之前弱分类器分类效果较差的数据的概率。最终的分类器是弱分类器线性组合。
损失函数:
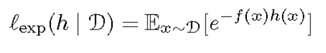
最终分类器H(x)

新分类器组合公式:
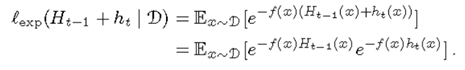
Gradient在函数空间沿着负梯度方向选取弱学习器来优化损失函数,适用于任意可以微分的损失函数。
AdaBoost是Gradient Boosting的特例,Gradient Boost是AdaBoost的推广。AdaBoost是通过提升错分数据点的权重来定位模型的不足。Gradient Boost是通过梯度来定位模型的不足,即每一次建立模型是在之前建立模型损失函数的梯度下降方向。因此Gradient Boosting可以使用更多种类的目标函数。

三种特征选择方法对比
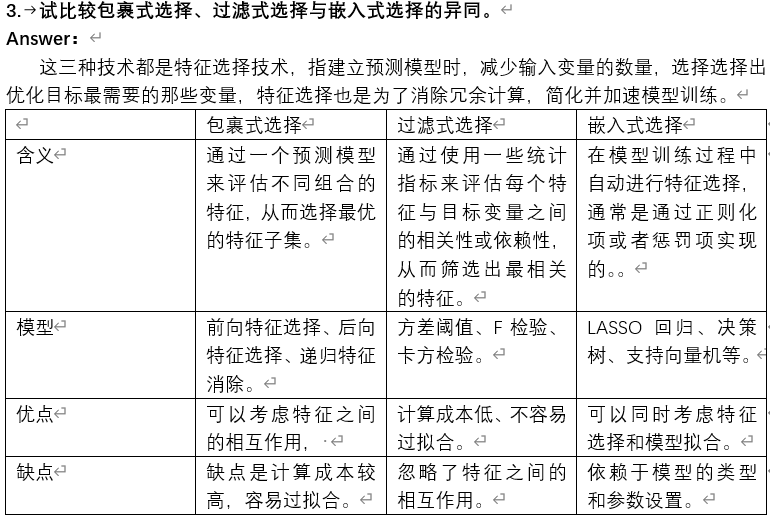
试述直接求解L0范数正则化会遇到的困难。
Answer:
L0范数正则化是一种用来实现特征选择和稀疏表示的方法,它的目标函数是最小化数据和其表示之间的误差,同时最小化表示的L0范数,也就是非零元素的个数。L0范数正则化的优点是可以得到最精确和最稀疏的表示。
但是,有以下几个缺点:
- 计算复杂度问题:L0范数正则化是一个NP-Hard问题,不存在一个多项式时间的而算法来找到最优解。这意味着只能使用启发式算法甚至穷举法来计算,这在数据量较大或者特征维度较高的情况下是不可计算的。
- 优化困难:L0范数正则化是非凸问题。因此其目标函数可能存在多个局部最优解,很多针对凸优化的高效的全局最优算法都无法使用,因此要求解L0范数正则化问题需要使用启发式算法进行近似计算从而避免陷入局部最优解。
- 算法稳定性差:L0范数正则化是一个不连续问题,因此其目标函数有一些点是不可导的,因此许多基于梯度的优化方法(例如梯度下降法、牛顿法)都不可使用。
试述为什么基于L1范数可以进行特征选择。
Answer:
基于L1范数的特征选择是一种稀疏正则化方法,它可以通过给模型的参数加上L1范数惩罚项一起优化达到约束的作用,使得部分参数变为0,从而实现特征选择,这样可以减少模型的复杂度,防止过拟合,提高泛化能力,也可以降低计算成本。
试比较K-SVD与K-Means方法的异同。
Answer:
两者关系为:
K-SVD和K-Means两者都是无监督学习算法,可以用来对数据进行字典学习或者数据聚类。K-means主要通过计算距离来分类,并不是利用DX来十分逼近原样本矩Y,从而主要用于聚类,而K-SVD则由一系列原子来线性组合逼近,因此相比K-means更适用于压缩,编码等应用。
两者差异为: