Math4ML 线性代数基础
Mathematics Foundation in Artificial Intelligence
Menu
共六部分:线性代数、矩阵分析、最优化问题、迭代优化算法、机器学习优化算法
其中线性代数8章:基础、线性空间、范数和逆矩阵、矩阵算子、矩阵分析、奇异值、特征值、矩阵分解。八、矩阵分解
LU分解、LDU分解、Cholesky分解
QR分解:实(复)非奇异矩阵A=正交阵(酉)Q · 实(复)非奇异上三角阵R
QR分解-Schmidt-gram正交化
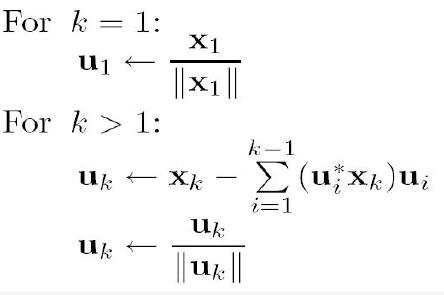
案例:最小二乘解

QR分解-Household:Householder矩阵即初等反射变换,对称、正交、自逆(逆矩阵等于自身)、对合(自己乘自己得单位阵)。
QR分解-Givens:Givens矩阵即旋转矩阵,是正交阵。
基础:

满秩分解
一个不满秩的矩阵,可以分解为两个满秩矩阵的乘积
$A \in C_c^{m\times n} = F\in C_r^{m\times r} G\in C_r^{r\times n}$
七、特征值及其估计
基本的结论:

定理3:Schur不等式:特征值绝对值的平方和小于等于F范数的平方,即所有元素的平方和。当A为正规矩阵的时候取等号。
Gerschgorin Theorem
1 所有特征值都在n个盖尔圆的并集之内。
2 k个盖尔圆构成的连通区域内有且仅有k个特征值。
Rayleigh商
六、奇异值
矩阵的条件数:cond(A) = ||A||2 · ||A^-1||2
矩阵的正交对角分解,对于非奇异方阵A,存在正交阵P、Q使得PTAQ=diag(ai)
奇异值与范数:矩阵的谱范数等于最大奇异值 $||A||_2 = \sigma_1$。
奇异值与行列式:矩阵的行列式的绝对值 = 奇异值的乘积
奇异值与条件数:cond($A^HA)=\frac{\sigma^2_1}{\sigma_n^2}$=cond(A)^2,矩阵的条件数大于等于 最大奇异值 / 最小奇异值。
奇异值与特征值:矩阵的特征值的绝对值,介于最小奇异值和最大奇异值之间。
五、特殊矩阵
对称矩阵和Hermitian Matrix:
复数域的共轭对称的矩阵
性质:
- 对所有$x \in C^n, x^HAx$为实数
- iA为斜Hermitian矩阵(skewhermitian matrix,又叫反Hermitian矩阵(antihermitian matrix))
- 任一矩阵,$A-A^H$为Hermitian矩阵
- 任一复矩阵,都可以唯一分解为$A=B+jC, B=1/2(A+A^H), C=1/(2j)(A-A^H)$
正交矩阵和酉矩阵:
性质:
- 向量经过酉变换,模长不变,向量范数不变
- 一对向量经过酉变换,内积不变,夹角不变
- 酉等价:$B=U^H AU$,F-范数相等
正规矩阵:$A^HA=AA^H$
Hermitian矩阵,斜Hermitian矩阵,酉矩阵都是正规矩阵。
相似矩阵与合同矩阵
相似矩阵具有相同的:特征值、行列式、特征多项式、迹;相似矩阵的幂也相似;
酉相似变换:经过酉矩阵的相似变换,得到对角矩阵,对角线元素即为特征值。
特殊矩阵:
置换矩阵:是一种每行每列都只有一个非零且为1的元素的方阵。
--1 交换矩阵:针对向量;
--2 互换矩阵:反对角线都为1,把矩阵的行或者列反转,又叫反射矩阵或后向单位矩阵;
--3 移位矩阵:单位矩阵的对角线循环右移。
--广义置换矩阵。
符号矩阵:对角线取1或者-1的对角矩阵。
中心化矩阵:
Vandermonde矩阵
Hadamard矩阵:所有元素取+1或者-1且H^T H = HH^T=nI的方阵。
Hadamard矩阵的构造
Toeplitz矩阵:任何一条对角线的值都相同,总共有2n-1个不同的值。
Hankel矩阵
四、矩阵的各种运算
矩阵的直和(direct sum) A$\oplus $B:就是把矩阵A和矩阵B放在一个分块矩阵的对角线,in my opinion 很像列向量或行向量组的扩展,其性质可想而知。
直和的迹=迹的和
直和的秩=秩的和
直和的行列式=行列式的积
矩阵的Hadamard积 A*B (又称 Schur积、对应元素乘积):
若矩阵A, B都是positive definite(positive semi-definite),它们的Hadamard product也是positive definite(positive semi-definite)
Kronecker积 A$\otimes $B (又叫直积(direct product)、张量积(tensor product)、矩阵外积):
两个矩阵之间的运算,其结果是一个新的矩阵,其行数等于第一个矩阵的行数乘以第二个矩阵的行数,列数等于第一个矩阵的列数乘以第二个矩阵的列数。
右Kronecker积:矩阵A的每一个元素都乘以矩阵B,这样得到的shape.A 个的B.shape大小的矩阵合成一个分块矩阵 (aij B)ij 。
向量的外积(又叫)
广义Kronecker积
Khatri-Rao积(又叫对应列Kronecker积)A$\odot$B
矩阵的向量化$vec(A)$,线性变换,把n列首尾衔接得到mn行一列的向量,
向量的矩阵化,反过来,对列向量矩阵化则是上述逆过程,行向量则是一行一行转为矩阵。
稀疏向量与稀疏表示:最小化0范数或者2范数,以Ax=y为约束,其中y为信号向量,x为转换后的稀疏向量,也是系数向量。
稀疏编码:给定一组向量X,确定基矩阵A和系数矩阵S使得近似地X=AS,并且系数矩阵每一列都是稀疏向量。
压缩感知
三、导出范数、矩阵的秩、迹、逆与广义逆。
计算题:矩阵范数、导出范数、广义逆。
1. 从属范数:一种由单位元思想引出的概念,单位矩阵在矩阵乘法中,如同1在数的乘法中的作用,但是否有一种矩阵范数,可以让单位矩阵的范数等于1?
下属公式定义了这样的范数,||·||是C^nxn上与向量范数||·||v相容的矩阵范数且||I||=`,称之为由向量范数||·||v导出的矩阵范数,或称属于向量范数||·||v的矩阵范数,简称导出范数或从属范数。
其中sup指上确界。

由向量范数导出的矩阵范数(从属范数):
一下三个导出范数均为非负,其中2-norm的lambda的绝对值称为谱半径。

矩阵2-范数的性质:
非方阵的矩阵范数:
矩阵范数的相容性、与向量范数的相容性。
从属范数
其中常见矩阵范数,它们的 酉不变性和相容性

计算案例:

Positive Define: 矩阵的正定性
Determint矩阵的特征值
矩阵的行列式
trace: 矩阵的迹

rank 矩阵的秩:

矩阵的逆
Sherman-Morrion矩阵求逆引理及其推广
分块矩阵求逆公式
左逆(left inverse)和右逆
矩阵的广义(伪)逆 $A^ {\dag }$、左伪逆、右伪逆
Penrose广义逆(Moore-Penrose逆),四种Penrose方程。
奇异值的定义
二、赋范空间与范数
赋范空间是定义了数域K上的范数的线性空间V,其中的范数是V→R的函数,具有非负性、齐次性($||c \alpha||=|c| ||\alpha||$)、三角不等式(Triangle Inequality)三个特性。
范数(vector norms)的几何特性可以直接通过图像来看:

常见向量范数

距离(distance):范数是一种度量,通过范数可以定义向量空间V的向量之间的距离||$\alpha - \beta$||:记作d($\alpha, \beta$),距离是一个二元函数V×V→R,具有非负性、同一性(距离为0的两个向量即相同)、对称性、三角不等式。
度量空间:通过距离可以定义度量空间,度量空间就是定义了度量的集合,每个赋范空间都是度量空间:$d(\alpha \times \beta)=||\alpha - \beta||$。
内积空间V中的线性无关向量组alpha,经过Schmidt正交化可以转化为与之等价的正交向量组beta,在V中没有非零向量与该正交组的没一个向量正交,就称该正交向量组beta为完备正交系。
常见的完备正交系:
Legendre多项式
Chebyshev多项式

酉不变范数的概念
矩阵范数(Matrix Norms):矩阵范数具有四个特性,在向量范数的基础上多了相容性(Compatible)的要求,即“对任意A,B$\in C^{n \times n}$,都有||AB||<=||A|| ||B||”。
以下列举Matrix 1-norm, Matrix inf-norm, Frobenius Matrix Norm:
(方阵范数)
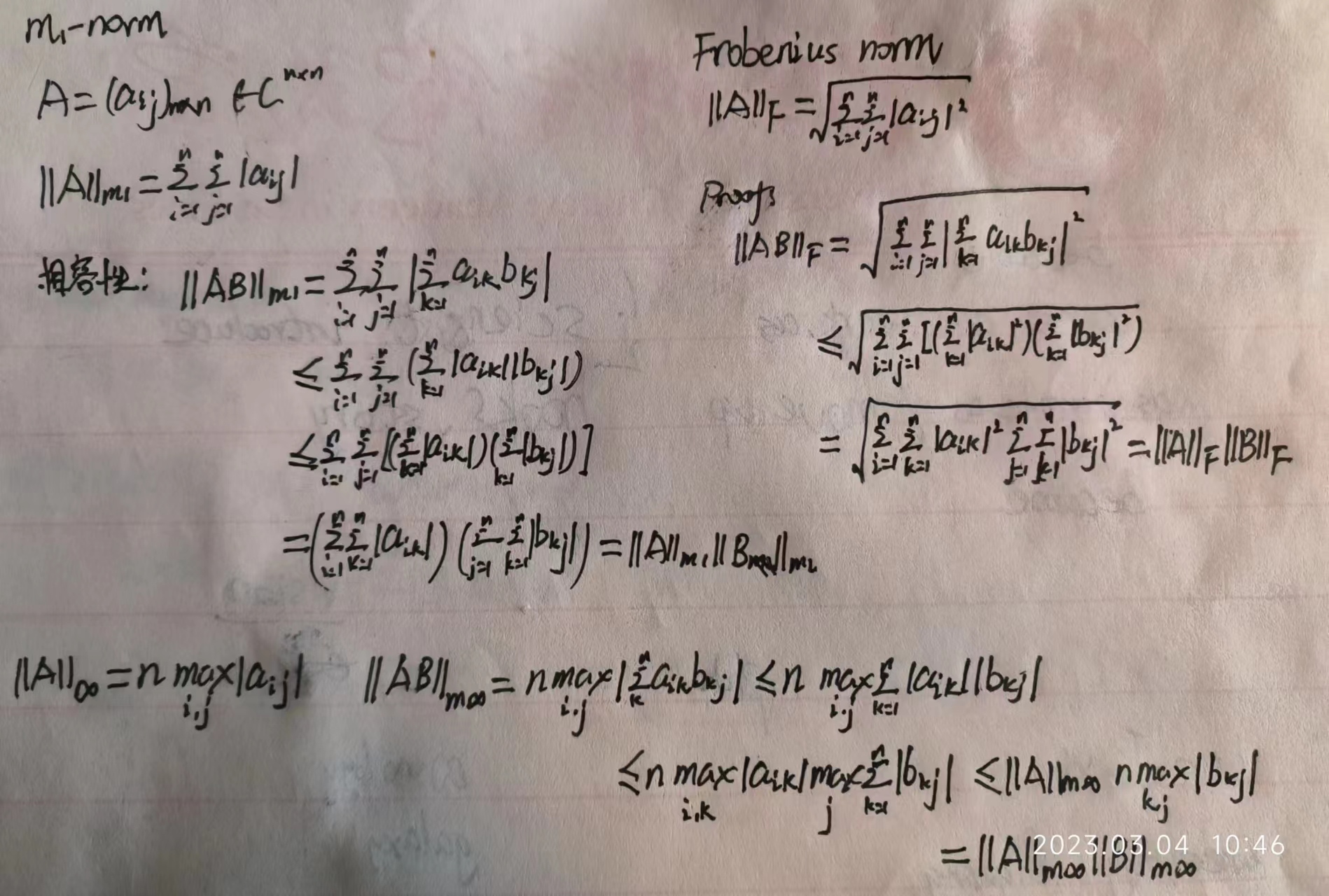
矩阵范数与向量范数之间相容:||$Ax||_v \leq ||A||_m||x||_v$。
1.与一个矩阵范数相容的向量范数不唯一。
2.对于一种矩阵范数,必存在与之相容的向量范数。

一、线性代数基础
数域K是定义了加法和乘法的一些数的集合,加法和乘法都满足结合律、交换律,其中乘法对加法满足分配律,数0和1都在K中,每个数都有唯一的逆元和负元。
数域K中的n个数组成的有序组称为“数域K上的n维向量”,默认写作列向量。
数域K上所有的n维向量的集合V,以及向量的加法和数乘运算一起构成数域K上的n维向量空间(Vector Space)。
数域K上的线性空间V需要满足:对加法和数乘封闭,对加法满足结合律和交换律,对加法存在零元和唯一负元,数乘对向量加法满足分配律,实数加法对数乘满足分配律,实数乘法对数乘满足结合律,数乘存在单位元。
向量空间V中最大线性无关组的向量个数称为向量空间V的维数,记作dim(V)。
数域K上的线性空间V中的“可以表示V中的任意向量的一组线性无关的向量”称为V的基。
复数集合V:1. 在复数域上的线性空间是1维的,任一既不是实数也不是虚数的复数都可以独自构成一组基;在实数域上的线性空间是2维的,任意两个非0且不相等的复数都是一组基。
向量之间的比较:只有维度相同的时候可以比较,如果某一向量的所有元素都大于零一元素对应位置的数值,则为大于。某一向量的任一元素都为正数,记为大于0。
当用n个实数来表示“向量空间V中某一组基下的n维向量v”时,这n个实数称作向量v的坐标。记作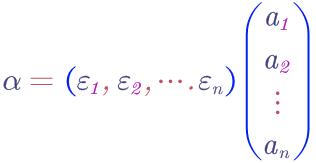
同一个线性变换在不同基下的矩阵是相似的。
【线性变换与线性映射在不同基偶与基下的关系 - T1me1s一exam1ner的文章 - 知乎(https://zhuanlan.zhihu.com/p/397542036)】
欧式空间中,正交向量组线性无关。Proof:用这组基的线性组合来表示任意向量,然后用任一分量与该向量做内积,结果剩下该分量与自己的内积,其系数显然为0。
如果线性变换能够保持向量的模长不变,那么内积也不变,这种线性变换称为正交变换。
正交变换一定可逆,两类正交变换:旋转(+1)和镜面反射(-1)。




