音频信号处理基础

用librosa库 读取音频：x, sr = librosa.laod(audio_path)

输入文件路径，返回数组和采样率。

import librosa
audio_path = './000085.wav'
x, sr = librosa.load(audio_path)  # [sr=44100]   # 22kHz default
print(type(x), type(sr))
print(x.shape, sr)

output:

<class 'numpy.ndarray'> <class 'int'>
(52920,) 2205

用wavio库 读取音频：wavio.read(audio_path)

import wavio
import numpy as np

path0 = "./000085.wav"  # normal wave
wav_struct = wavio.read(path0)
print("wav_struct:")
print(wav_struct)
wav = wav_struct.data.astype(float) / np.power(2, wav_struct.sampwidth*8-1)
print("wav:")
print(wav)

output:

wav_struct:
Wav(data.shape=(105840, 2), data.dtype=int16, rate=44100, sampwidth=2)
wav:
[[ 0.00000000e+00  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00]
 [-3.05175781e-05 -3.05175781e-05]
 ...
 [ 0.00000000e+00  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00]]

播放音频：

import IPython.display as ipd
ipd.Audio(audio_path)
# 或者 ipd.Audio(x, rate=sr)

绘制波形图：

振幅随时间的变化

import matplotlib.pyplot as plt
import librosa.display
plt.figure(figsize=(14, 5))
librosa.display.waveplot(x, sr=sr)

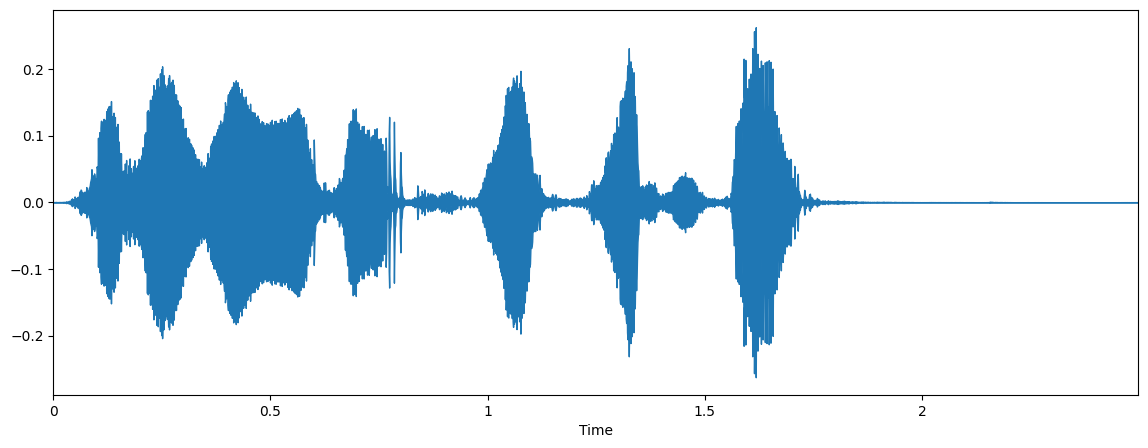
语音信号波形图

短时傅里叶变换 STFT和频谱图 scipy.signal

import librosa
import matplotlib.pyplot as plt
import scipy.signal as sgn

path0 = "./000085.wav"
x, sr = librosa.load(path1)

# signal.stft(x, **params)
# params: -fs sampling rate; -window ; ...
# f: 采样频率数组; t:段时间数组 ; zxx: stft result
f, t, zxx = sgn.stft(x, fs=sr)
def stft_specgram(picname=None, **params):
    plt.figure(0)
    plt.pcolormesh(t, f, np.abs(zxx))
    plt.colorbar()
    plt.title("STFT Magnitude")
    plt.xlabel("Frequency [Hz]")
    plt.ylabel("Time [sec]")
    plt.tight_layout()
    if picname is not None:
        plt.savefig("./"+picname+"-stft-res.png")
    # plt.clf()
stft_specgram("000072")

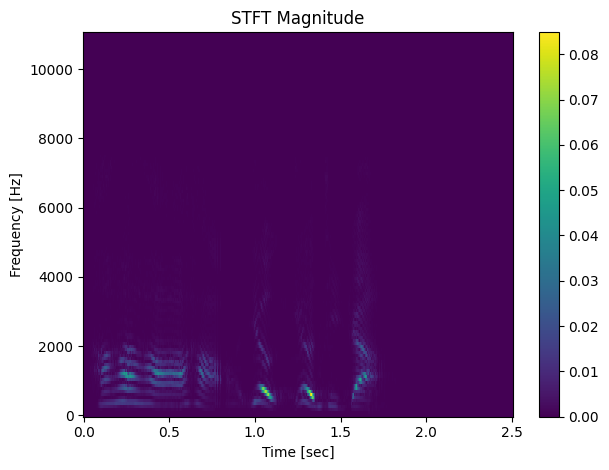
语谱图

绘制谱图 librosa

X = librosa.stft(x)
Xdb = librosa.amplitude_to_db((abs(X)))
plt.figure(1, figsize=(14, 5))
# 纵轴表示频率（从0到10kHz），横轴表示剪辑的时间。
librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='hz')
plt.colorbar()

傅里叶变换：将复合波形拆解还原成每个频率上的单一正弦波构成，相当于把二维的波形图往纸面方向拉伸，变成了三维的立体模型，而拉伸方向的轴就是频率，从小到大每个频率点上都对应着一条不同幅值和相位的正弦波。

从时域变换到频域，即横坐标为频率，纵坐标为该频率对应的振幅（频谱图）。

波形实质上是将各个频率的波形叠加在了一起，即波形是由各频率不同幅值和相位的简单正弦波复合叠加得到的。

频带 frequency band指允许传送的信号的频率范围。

带宽 band width 指为保证发射信息的速率和质量所需占据的频带宽度容许值（Hz kHz MHZ）。

Reference

音频特征（2）：时域图、频谱图、语谱图（时频谱图）：https://blog.csdn.net/Robin_Pi/article/details/109204672

傅里叶变换——另一种世界观：https://www.cnblogs.com/hizhaolei/p/8051485.html

短时傅里叶变换：https://www.cnblogs.com/byeyear/p/6129385.html

短时傅里叶变换(Short Time Fourier Transform)原理及 Python 实现：https://www.cnblogs.com/klchang/p/9280509.html

【Python】librosa音频处理教程：https://blog.csdn.net/fengdu78/article/details/124875505