【最优化】简单线搜索（黄金分割法，斐波那契法，固定步长法......）

黄金分割法（Golden Section Method）和斐波那契法（Fibonacci Method）极为相似，唯一的区别就是试探点的公式不一样而已。相比较，斐波那契法更为灵活更为强大。斐波那契法介于二分搜索和黄金分割法之间。

Fibonacci数列：1，1，2，3，5，8，13，21，34，55，89，144......

可见，相邻两项的比值从0.5渐渐变为0.618并趋近于0.618。

而固定步长法(Fixed Step Method)其实就是线搜索里面的“进退法”。

一、进退法（Fixed固定步长法）

选取初始值和固定的步长，然后向前计算试探点及其函数值，找到最低点直到该方向的函数值变大而停止迭代。

二、黄金分割法的算法如下：

三、斐波那契法算法如下：

 

Python程序：

所用函数如下：

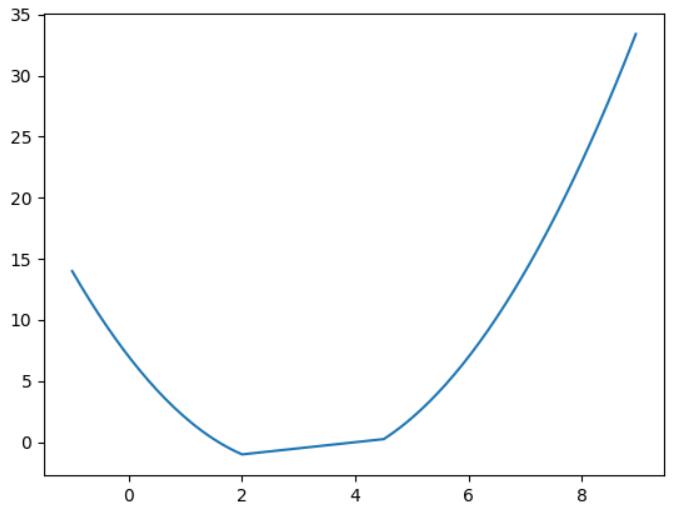
f(x)=min{x/2, 2-(x-3)^2, 2-x/2}

# -*- coding: utf-8 -*-
# @Author : ZhaoKe
# @Time : 2022-10-09 15:29
import numpy as np
import matplotlib.pyplot as plt

def fun(x):
    f1 = x / 2
    f2 = 2-(x-3)**2
    f3 = 2-x/2
    f = np.vstack((f1, f2, f3))
    # print(f)
    return -np.min(f, axis=0)


def fun_grad(x):
    return [2*x[0], 2*x[1]]

def golden_section(f, left, right, eps):
    print("===========Golden Section Search==========")
    lam = left + 0.382*(right-left)
    mu = left + 0.618*(right-left)
    k = 1
    tol = right - left
    flam, fmu = 0, 0
    while tol > eps and k < 100000:
        flam = f(lam)
        fmu = f(mu)
        print("k=", k)
        print(f"lam={lam}, mu={mu}, flam={flam}, fmu={fmu}")
        if flam > fmu:
            left = lam
            lam = mu
            mu = left + 0.618*(right-left)
        else:
            right = mu
            mu = lam
            lam = left + 0.382*(right-left)
        k = k + 1
        tol = np.abs(right-left)
        print(f"left={left}, right={right}")
    if k == 100000:
        print("找不到最小值")
        x = None
        minf = None
        return
    x = (left + right) / 2
    min_f = f(x)
    print("极值点：", x, "，函数值: ", min_f)


def fibonacci_search(f, left, right, eps):
    print("===========Fibonacci Search==========")
    N = (right-left) / eps
    n = 1
    Fib = [1, 1]
    c = Fib[1] - N
    flam, fmu = 0, 0
    while c < 0:
        n += 1
        Fib.append(Fib[n-1] + Fib[n-2])
        c = Fib[n] - N
    print(Fib[0:12])
    lam = left + Fib[n-2]/Fib[n] * (right - left)
    mu = left + Fib[n-1]/Fib[n] * (right - left)
    k = 1
    while k < n-3:
        flam = fun(lam)
        fmu = fun(mu)
        if flam > fmu:
            left = lam
            lam = mu
            mu = left + Fib[n-1-k]/Fib[n-k] * (right-left)
        else:
            right = mu
            mu = lam
            lam = left + Fib[n-2-k]/Fib[n-k] * (right-left)
        k += 1
    x = (left + right) / 2
    min_f = f(x)
    print("极值点：", x, "，函数值: ", min_f)


def fixedStepMethod(f, left, right, eps):
    print("===========Fixed Step Search==========")
    delta_s = 2
    dire = 1
    alpha = 1
    x0 = (left + right)/2
    old_x0 = None
    new_x0 = x0 + delta_s
    fx0 = f(x0)
    fx1 = f(new_x0)
    # print(f"fx0={fx0}, fx1={fx1}")
    k = 0
    x_list = [x0, new_x0]
    while True:
        fx0 = fx1
        fx1 = f(new_x0)
        if fx1 < fx0:
            # print("fx1 < fx0")
            alpha += 1
            delta_s = delta_s + dire * alpha * delta_s
            old_x0 = x0
            x0 = new_x0
            new_x0 = x0 + delta_s
            k += 1
        else:
            # print("fx1 >= fx0")
            if k == 0:
                # print("--k=0---")
                dire = -dire
                delta_s = delta_s + 2*dire * alpha * delta_s
                old_x0 = x0
                new_x0 = x0 + delta_s
                fx1 = f(new_x0)
                k = 1
            else:
                # print('--k>0--')
                left = old_x0 if old_x0 < new_x0 else new_x0
                right = old_x0 if old_x0 > new_x0 else new_x0
                break
        x_list.append(new_x0)
        # print("k: ", k)
        # print(f"old x new={old_x0},{x0},{new_x0}")
        # print(f"f0 f1={fx0}, {fx1}")
        # print("step", delta_s)
    # print(left, right)
    x_min = (left + right) / 2
    f_min = f(x_min)
    print(f"x={x_min}, f={f_min}")
    # plt.figure(0)
    # p_x = np.arange(-1, 9, 0.05)
    # p_y = fun(p_x)
    # plt.plot(p_x, p_y)
    # plt.plot(x_list, f(np.array(x_list)))
    # plt.show()

def draw():
    plt.figure(0)
    p_x = np.arange(-1, 9, 0.05)
    p_y = fun(p_x)
    plt.plot(p_x, p_y)
    plt.show()


if __name__ == '__main__':
    golden_section(fun, 0, 8, 0.05)
    fibonacci_search(fun, 0, 8, 0.05)
    fixedStepMethod(fun, 0, 8, 0.05)
    # draw()

 

计算结果：

C:\Users\zhaoke\.conda\envs\tacotron2cn\python.exe D:/PythonWorkspace/tacotron2cn/course-optimization/unconstrained/GoldenFibonacci.py
===========Golden Section Search==========
left=1.993884615308544, right=2.0341002823564076
极值点： 2.013992448832476 ，函数值:  [-0.99300378]
===========Fibonacci Search==========
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144]
极值点： 1.9742489270386265 ，函数值:  [-0.94783474]
===========Fixed Step Search==========
x=3.0, f=[-0.5]

显然两个算法所得结果都与真实值极为相近（见上图。）