LU分解的C++实现

　　又是一次数值科学与计算方法的实验题目，LU分解的推导就不赘述，其核心公式如下：

$u_{1i}=a_{1i}   (i=1,2,3,\cdots ,n) $

$l_{i1}=a_{i1}/u_{11} ( i=2,3,\cdots ,n)$

$u_{ri}=a_{ri}-\sum_{k=1}^{r-1}l_{rk}u_{ki}    (i=r,r+1,r+2,\cdots ,n)$

$l_{ir}=(a_{ir}-\sum_{k=1}^{r-1}l_{ik}u_{kr}) /u_{rr}    (i=r+1,\cdots ,n;且r\ne n)$

　　C++实现方面，首先LU分解的函数传入两个参数，方阵的一阶数组和方阵的阶数（方阵用一维数组的行优先表示）。

　　计算步骤：

　　1. 初始化LU矩阵，L矩阵上三角为0，对角线为1，U矩阵下三角为0.

　　2. 计算U矩阵的第一行和L矩阵的第一列

　　3. 循环计算U矩阵和L矩阵，第一层循环表示U计算到第几行，同时也表示L计算到第几列，先计算U后计算L。第二层循环分别表示U矩阵改行的第几列元素。第三层循环就是公式中的求和符号部分。

程序如下：

#include <iostream>

// 参数：一个order阶矩阵，和矩阵的阶数
void lowerUpperFactor(double *matrix, int order) {
    printf("--------原矩阵：--------\n");
    printMatrix(matrix, order,order);
    
    // 结果变量  L矩阵和U矩阵都是order阶矩阵
    double *L = new double[order*order];
    double *U = new double[order*order];

    // 初始化全为0
    for (int i = 0; i < order; i++) {
        // 初始化U下三角为0
        for (int j = 0; j < i; j++) {
            *(U + i * order + j) = 0;
        }
        //初始化L对角线为1，上三角为0
        *(L + i * order + i) = 1;
        for (int j = i + 1; j < order; j++) {
            *(L + i * order + j) = 0;
        }
    }
    // 计算U的第一行和L的第一列
    int i = 0;
    for (i = 0; i < order; i++) {
        *(U + i) = *(matrix + i);
    }
    for (i = 1; i < order; i++) {
        *(L + i * order) = *(matrix + i * order) / *U;
    }
    // 计算其余行列
    int temp;
    for (int i = 1; i < order; i++) {
        // 计算矩阵U
        for (int j = i; j < order; j++) {
            temp = 0;
            for (int k = 0; k < i; k++) {
                temp+= (*(U + k * order + j) * (*(L + i * order + k)));
            }
            *(U + i * order + j) = *(matrix + i * order + j) - temp;
        }
        // 计算矩阵L
        for (int j = i+1; j < order; j++) {
            temp = 0;
            for (int k = 0; k < i; k++) {
                temp += *(U + k * order + i) * (*(L + j * order + k));
            }
            *(L + j * order + i) = (*(matrix +j * order + i) - temp) / (*(U+i* order + i));
        }
    }

    printf("------矩阵U------\n");
    printMatrix(U, order,order);
    printf("------矩阵L------\n");
    printMatrix(L, order, order);

    if (L) {
        delete[] L;
    }
    if (U) {
        delete[] U;
    }
}

void printMatrix(double *matrix, int row, int column) {
　　for (int i = 0; i < row; i++) {
　　　　for (int j = 0; j < column; j++) {
　　　　　　printf("%6.2lf ", *(matrix + i * column + j));
　　　　}
　　　　printf("\n");
　　}
}

int main() {

    //double matrix[] = { 1,2,3,2,5,2,3,1,5 };
    //int order = 3;
    double matrix1[] = { 1,1,-1,2,1,2,0,2,-1,-1,2,0,0,0,-1,1 };
    int order1 = 4;

    lowerUpperFactor(matrix1, order1);
}

提供两个算例验证其正确性和通用性：

1. 这个取自《数值分析》第四版孙家广中的例题

通过程序计算如下：

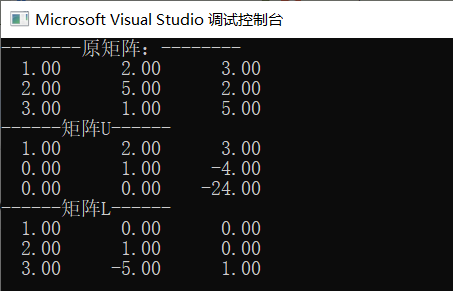
2. 这个取自《Numerical Analysis-Burden Faires》中的例题

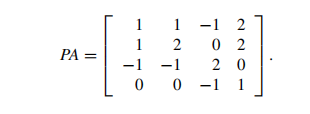
程序计算如下：