求0到n之间素数个数的序列(Java)

要求：

(1) 找出0-1000之间素数
(2) 设f(n)表示0-n之间的素数个数，计算出当n=0,1,2,3,.....,997时f(n)的值，并写入文件

分析：

　　首先找素数使用一个效率较高的方法——Eratosthenes筛法，只要把1和不超过1000的正合数都删去。其原理为：由于正合数必有不可约数是小于等于其平方根的，只要首先求出1-1000平方根之间的全部不可约数，依次把这些不可约数之外的倍数也全部删去，剩下的正好就是不可约数。（参考《初等数论》）

其程序如下：

    /**
     * @param sieveSize: int 素数表的长度
     * @return 素数表
     */
    public ArrayList<Integer> primeSieve(int sieveSize){
        boolean[] sieve = new boolean[sieveSize];
        // 初始化都是素数
        for (int i = 2; i < sieve.length; i++) {
            sieve[i] = true;
        }
        sieve[0] = false;
        sieve[1] = false;
        // 筛选
        int pointer;
        for (int i = 2; i < (int)Math.sqrt(sieveSize)+1; i++) {
            pointer = i*2;
            while (pointer < sieveSize) {
                sieve[pointer] = false;
                pointer+=i;
            }
        }
        // 返回素数
        ArrayList<Integer> primes = new ArrayList<Integer>();
        for (int i = 0; i < sieveSize; i++) {
            if(sieve[i]==true)
                primes.add(i);
        }
        return primes;
    }

　　有了素数表，求f(n)就容易多了，但是只要遍历0-997，每一轮循环判断一下循环变量是否等于素数表中的某个数，等于就把当前f(n)设为某个数，否则等于前一个数，然而这样效率太低了，事实上素数表是有序的，只要不断遍历素数表相邻两个数为区间的序列，就能实现一次遍历完不需要判断
代码如下：

传入的参数array是素数表，len是所求序列的长度

    public int[] countPrime(int[] array, int len) {
        int[] result = new int[len];
        result[0] = 0; result[1] = 0;
        int begin, end;
        int i = 2;
        for (int j = 0; j < array.length-1; j++) {
            
            begin = array[j];
            end = array[j+1];
            result[i] += result[i-1]+1;
            
            System.out.printf("=====result[%d] = %d \n", i, result[i]);
            i++;
            begin++;
            while (begin < end) {
                result[i] = result[i-1];
                System.out.printf("result[%d] = %d \n", i, result[i]);
                begin++;
                i++;
            }
        }
        result[i] += result[i-1]+1;
        System.out.printf("=====result[%d] = %d \n", i, result[i]);
        return result;
    }

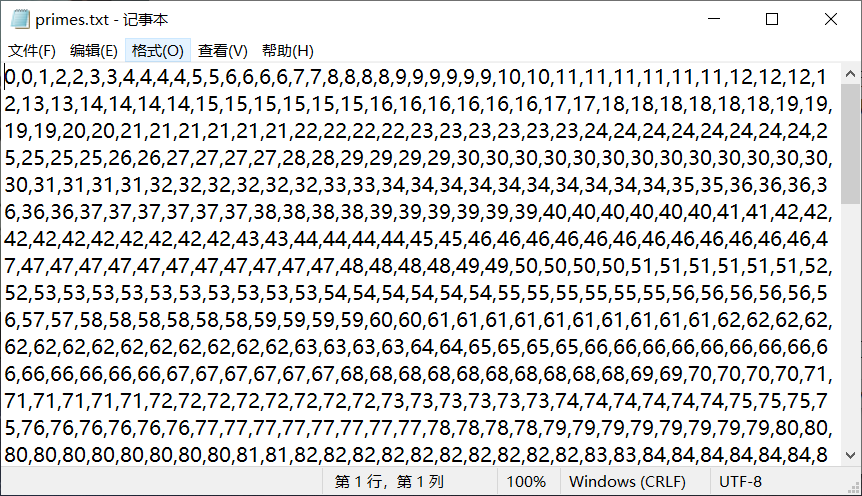
　　把所求结果写入文件：经典的File+FileWriter+BufferedWriter即可，写入主函数

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        CryptoTechnology ct = new CryptoTechnology();
        int maxNum = 1000;
        System.out.println(maxNum + "以内的素数有：");
        ArrayList<Integer> tableList= ct.primeSieve(maxNum);
        ct.printIntegerList(tableList);
        int[] tablearray = new int[tableList.size()];
        int index = 0;
        Iterator<Integer>it = tableList.iterator();
        while (it.hasNext()) {
            Integer integer = (Integer) it.next();
            tablearray[index++] = integer;
        }
        int[] counter = ct.countPrime(tablearray, maxNum);
        String content = "";
        for (int i = 0; i < counter.length; i++) {
            content += counter[i]+",";
        }
        System.out.println(content);
        
        File file = new File("src/zhaoke/primes.txt");
        FileWriter fw;
        try {
            fw = new FileWriter(file);
            BufferedWriter bw = new BufferedWriter(fw);
            bw.write(content);
            bw.close();
            fw.close();
        } catch (FileNotFoundException e) {
            // TODO Auto-generated catch block
            e.printStackTrace();
        } catch (IOException e) {
            // TODO Auto-generated catch block
            e.printStackTrace();
        }
    }

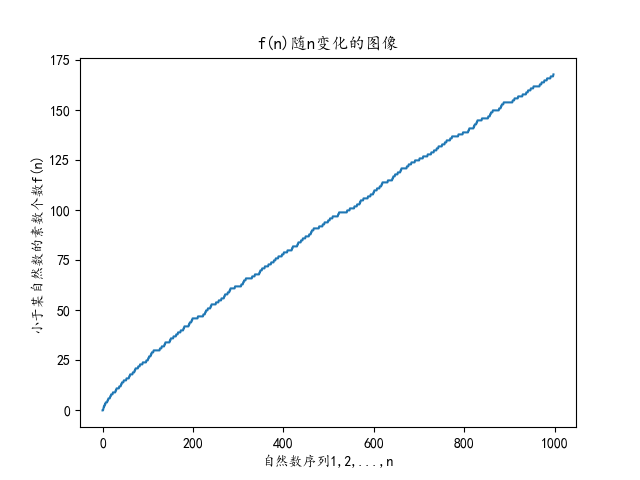
求出结果得到一个文件，也就是F(n)随n变化的序列。

求出结果可以试试给f(n)画个图，使用python就很容易了，代码如下：

import matplotlib.pyplot as plt

# 读取文件，得到一个字符串
with open('primes.txt') as f:
    line = f.readline()
f.close()

primes = line.split(',')  # 字符串分割
primes = list(map(int, primes))  # 字符串列表转换为int列表
x = range(len(primes))
plt.plot(x, primes)  # 画图

# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['KaiTi']  # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False  #

plt.title('f(n)随n变化的图像')
plt.xlabel('自然数序列1,2,...,n')
plt.ylabel('小于某自然数的素数个数f(n)')

plt.show()

如图：