力扣78题、77题、90题、491题（回溯算法、子集组合）

78、子集

基本思想：

回溯算法

具体实现：

这道题没有if判断递归是否结束

因为这个是每递归一下就加入到结果数组中，

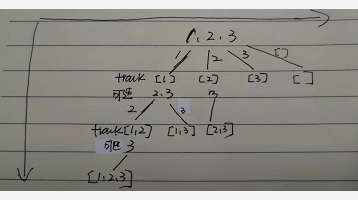
代码： 

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> subsets(int[] nums) {
        if (nums.length == 0){
            result.add(new ArrayList<>());
            return result;
        }
        subsetsHelper(nums, 0);
        return result;
    }
    private void subsetsHelper(int[] nums, int startIndex){
        result.add(new ArrayList<>(path));
        for (int i = startIndex; i < nums.length; i++){
            path.add(nums[i]);
            subsetsHelper(nums,i+1);
            path.removeLast();
        }
    }
}

 

77、组合

基本思想：

回溯算法

具体实现：

1、组合是不能有重复的

递归函数的参数每次就有起始数，

for循环从start开始递增

上述两个操作保证了不会有重复

2、递归结束条件是到达叶子节点

 

 

代码：

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        combineHelper(n, k, 1);
        return result;
    }
    public void combineHelper(int n, int k, int start) {
        if (path.size() == k) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = start; i <= n; i++) {
            path.add(i);
            combineHelper(n, k, i + 1);
            path.removeLast();
        }
    }
}

 

剪枝:

 

 具体实现：

k-len(track)是track中还差的元素个数

n-(k-len(track))+1是要达到组合中元素为k，至多开始的位置

比如：n=4，k=3 ，track里面啥也没    4-3+1=2

          意思是最多从2开始，组合可以是2,3,4

          再循环到3不可能满足组合个数

python写到代码里n-(k-len(track))+2 因为range的第二个参数代表第一个不取的数

代码：

class Solution {
    List<List<Integer>> result  = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        combineHelper(n, k, 1);
        return result;
    }
    private void combineHelper(int n, int k, int startIndex){
        if (path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){
            path.add(i);
            combineHelper(n, k, i + 1);
            path.removeLast();
        }
    }
}

 

 90、子集II

基本思想：

回溯算法

与78题的区别是，子集需要去重

具体实现：

 

 

代码：

class Solution {
    List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
    LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果   
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        if (nums.length == 0){
            result.add(path);
            return result;
        }
        Arrays.sort(nums);//去重需要排序
        subsetsWithDupHelper(nums,0);
        return result;
    }
    private void subsetsWithDupHelper(int[] nums, int startIndex){
        result.add(new ArrayList<>(path));
        if (startIndex >= nums.length){
            return;
        }
        for (int i = startIndex; i < nums.length; i++){
            if (i > startIndex && nums[i] == nums[i - 1]){
                //我们要对同一树层使用过的元素进行跳过
                continue;
            }
            path.add(nums[i]);
            subsetsWithDupHelper(nums, i + 1);
            path.removeLast();
        }
    }
}

 

 

 

 

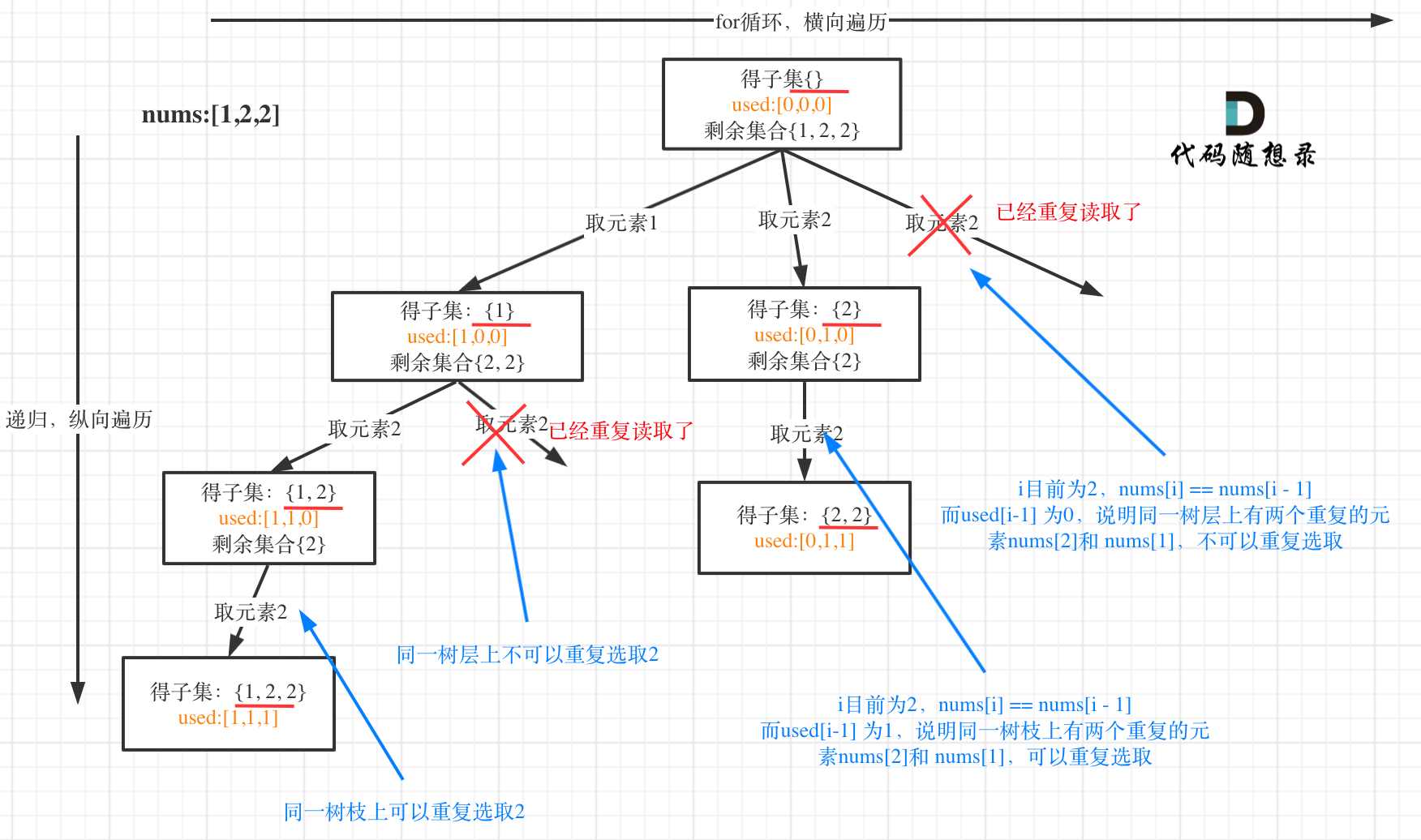
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> track = new LinkedList<>();
    boolean[] used;
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        used = new boolean[nums.length];
        traversal(nums, 0);
        return result;
    }
    public void traversal(int[] nums, int start) {
        result.add(new ArrayList<>(track));
        for (int i = start; i < nums.length; i++) {
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;
            //前面有相同的元素并且没有被使用过，那就是同一树层碰到相同元素了
            track.add(nums[i]);
            used[i] = true;
            traversal(nums, i + 1);
            track.removeLast();
            used[i] = false;
        }
    }
}

 

 491、递增子序列

基本思想：

回溯算法

与90题不同，90题需要排序，这道题不需要

90题判断是否重复是用nums[i] == nums[i-1]，这道题不行

具体实现：

 

 

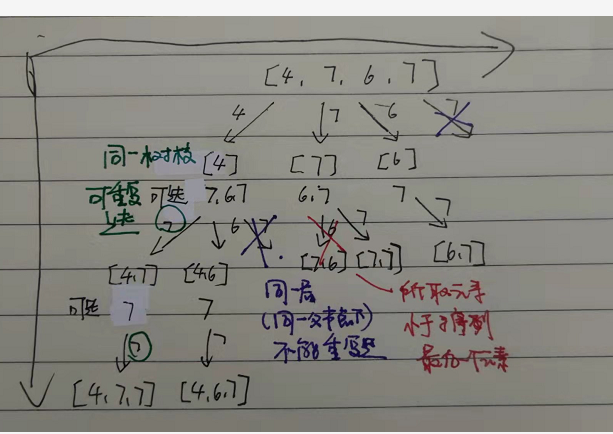
代码：

 

class Solution {
    private List<Integer> path = new ArrayList<>();
    private List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        backtracking(nums,0);
        return res;
    }

    private void backtracking (int[] nums, int start) {
        if (path.size() > 1) {
            res.add(new ArrayList<>(path));//注意这里不要加return，要取树上的节点
        }
    //记录[-100,100]这些数字出现的个数
    //[-100,100]对应索引[0,201]
        int[] used = new int[201];
        for (int i = start; i < nums.length; i++) {
            if (used[nums[i] + 100] == 1) continue;
            if (!path.isEmpty() && nums[i] < path.get(path.size() - 1)) continue;
            used[nums[i] + 100] = 1;//记录这个元素在本层用过了，本层后面不能再用了
            path.add(nums[i]);
            backtracking(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}