给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

/*
给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
*/
#include<stdio.h>
#include<math.h>

main()
{
    int n,rs=1;
    scanf("%d",&n);
    if(n==2){
        printf("1\n");
        return 0;
    }
    if(n==3){
        printf("2\n");
        return 0;
    }
    while(n>4){
        rs*=3;
        n=n-3;
    }
    printf("%d\n",rs*n);
}

### 解题思路
题目分析：
将正整数n拆分为特定整数x的和，并使这些特定整数n/x个x的乘积最大化，即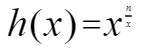
![h.png](https://pic.leetcode-cn.com/5de45ff139b93e7047f541a27259777bf3bf8dfd92dea3685f50960efd5f0b56-h.png)


数学推导：
h(x)=e^((n/x)lnx)与函数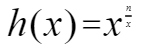
![h.png](https://pic.leetcode-cn.com/8104982928f2230b99701bad3b7f19bca7f6a8200b88ec737930c117b0097905-h.png)单调性相同，令f’(x0)=0，因为f’’(x0)<0，得极大值x0=e，则特定数x=e约等于2.78，整数化，x为2或3，又f(3)/f(2)>1,所以取x=3；

结论：
为了获取最大化的乘积，需要将n拆分更多的3，
令a=n/3；b=n%3；则n=a个3之和+b；
b分为0，1，2；
当b=0时，max=3^a;
当b=2时，max=3^a*2，若向前借一个2，变成2+3=5,5的最大乘积为3*2=6，为最大乘积，所以不变。
当b=1时，因为拆分为1，所以向前借一个3，变成3+1=4，4的最大乘积为2*2=4，若按原来为3*1=3就小了；所以max=3^(a-1)*4

再讨论n：
当n<=3,max=n-1；
当n>=4，按n%3=0，1，2余数分类

### 代码

```c
int integerBreak(int n){
    int i,rs=1;
    if(n==2) return 1;
    if(n==3) return 2;
    while(n>4){
        rs*=3;
        n-=3;
    }
    rs*=n;
    return rs;
}

 动态规划自底向上+递归自顶向下待学习！