25寒假济南集训day.3
上午
线段树例题
昨天没有讲完线段树的例题,只讲了几道
今天接着昨天的讲
例题1 P1471:
查询平均数就是求和再除以区间长度。
查询方差等价于查询区间平方和,想想怎么维护?
其实就是在问:怎么\(pushup\),怎么\(pushdown\)。
利用完全平方公式\(:(A+B)^2=A^2+2\times A\times +B^2\)
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 9;
int n, m;
double a[maxn];
double sum[maxn << 2], tag[maxn << 2],sq[maxn<<2];
int ls(int x) {
return x << 1;
}
int rs(int x) {
return x << 1 | 1;
}
void pushup(int x) {
sum[x] = sum[ls(x)] + sum[rs(x)];
sq[x]=sq[ls(x)]+sq[rs(x)];
}
void add(int x, int l, int r, double k) {
sq[x]+=2*k*sum[x]+(r-l+1)*k*k;
sum[x] += k * (r - l + 1);
tag[x] += k;
}
void pushdown(int x, int l, int r) {
int mid = (l + r) >> 1;
if (tag[x] != 0) {
add(ls(x), l, mid, tag[x]);
add(rs(x), mid + 1, r, tag[x]);
tag[x] = 0;
}
}
void build(int x, int l, int r) { // build(x, l, r) 当前节点编号为x,维护的区间[l,r]。
tag[x]=0;
if (l == r) {
sum[x] = a[l];
sq[x]=a[l]*a[l];
return ;
}
int mid = (l + r) >> 1;
build(ls(x), l, mid);
build(rs(x), mid + 1, r);
pushup(x);
}
double querySum(int x, int l, int r, int L, int R) {
// x 当前节点的编号
// l, r 当前节点维护的区间
// L, R 询问的区间
if (L <= l && r <= R) return sum[x];
pushdown(x, l, r);
int mid = (l + r) >> 1;
double ret = 0;
if (L <= mid) ret += querySum(ls(x), l, mid, L, R);
if (mid < R) ret += querySum(rs(x), mid + 1, r, L, R);
return ret;
}
double querySq(int x, int l, int r, int L, int R) {
// x 当前节点的编号
// l, r 当前节点维护的区间
// L, R 询问的区间
if (L <= l && r <= R) return sq[x];
pushdown(x, l, r);
int mid = (l + r) >> 1;
double ret = 0;
if (L <= mid) ret += querySq(ls(x), l, mid, L, R);
if (mid < R) ret += querySq(rs(x), mid + 1, r, L, R);
return ret;
}
void posAdd(int x, int l, int r, int p, ll k) {
if (l == r) {
sum[x] += k;
return ;
}
pushdown(x, l, r);
int mid = (l + r) >> 1;
if (p <= mid) posAdd(ls(x), l, mid, p, k);
else posAdd(rs(x), mid + 1, r, p, k);
pushup(x);
}
void intervalAdd(int x, int l, int r, int L, int R, double k) {
if (L <= l && r <= R) {
add(x, l, r, k);
return ;
}
pushdown(x, l, r);
int mid = (l + r) >> 1;
if (L <= mid) intervalAdd(ls(x), l, mid, L, R, k);
if (mid < R) intervalAdd(rs(x), mid + 1, r, L, R, k);
pushup(x);
}
signed main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
build(1, 1, n);
while (m--) {
int opt;
cin >> opt;
int x, y;
cin >> x >> y;
if (opt == 1) {
double k;
cin >> k;
intervalAdd(1, 1, n, x, y, k);
}
if (opt == 2) {
printf("%.4lf\n", querySum(1, 1, n, x, y)*1.0/(y-x+1));
}
if(opt==3){
double avg=querySum(1,1,n,x,y)*1.0/(y-x+1);
double sq=querySq(1,1,n,x,y)*1.0/(y-x+1);
// cout<<avg<<' '<<sq<<endl;
printf("%.4lf\n",sq-avg*avg);
}
}
return 0;
}
例题2 P3373:
增加了一个区间乘法,我们此时只需要思考怎么\(pushdown\)就行了。
我们之前的\(lazytag\)的表示方法是:把整个区间\(+k\)。
那么我们现在增加了乘法之后就是:把整个区间\(\times k + t\),也就是我们需要维护两个懒标记\(:k\)和\(t\)。
区间加法就是把加法标记\(t\)增加\(v\),也就是(把整个区间\(\times k + (t+v))\)
区间乘法就是把乘法标记和加法标记都乘\(v\),也就是(把整个区间\(\times k + t)\times v= (把整个区间\times (k\times v) + (t\times v))。\)
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int ksm(int a, int b, int p) {
if (b == 0) return 1;
if (b == 1) return a % p;
int c = ksm(a, b / 2, p);
c = c * c % p;
if (b % 2 == 1) c = c * a % p;
return c % p;
}
int n, m, q, a[100001], ll[500001], rr[500001], tja[500001], tah[500001], sum[500001];
int ls(int x) {
return x << 1;
}
int rs(int x) {
return x << 1 | 1;
}
void pushup(int x) {
sum[x] = (sum[ls(x)] + sum[rs(x)]) % m;
}
void build(int x, int l, int r) {
ll[x] = l, rr[x] = r;
tah[x] = 1, tja[x] = 0;
if (l == r) {
sum[x] = a[l] % m;
return ;
}
int mid = (l + r) >> 1;
build(ls(x), l, mid), build(rs(x), mid + 1, r);
pushup(x);
}
void tag_cheng(int x, int tag) {
(sum[x] *= tag) %= m;
(tah[x] *= tag) %= m;
(tja[x] *= tag) %= m;
}
void tag_jia(int x, int tag) {
(sum[x] += (rr[x] - ll[x] + 1) * tag % m) %= m;
(tja[x] += tag) %= m;
}
void pushdown(int x) {
if (tah[x] != 1) {
tag_cheng(ls(x), tah[x]);
tag_cheng(rs(x), tah[x]);
tah[x] = 1;
}
if (tja[x] != 0) {
tag_jia(ls(x), tja[x]);
tag_jia(rs(x), tja[x]);
tja[x] = 0;
}
}
void add_cheng(int x, int L, int R, int k) {
if (L <= ll[x] && rr[x] <= R) return tag_cheng(x, k);
pushdown(x);
int mid = (ll[x] + rr[x]) >> 1;
if (L <= mid) add_cheng(ls(x), L, R, k);
if (mid < R) add_cheng(rs(x), L, R, k);
pushup(x);
}
void add_jia(int x, int L, int R, int k) {
if (L <= ll[x] && rr[x] <= R) return tag_jia(x, k);
pushdown(x);
int mid = (ll[x] + rr[x]) >> 1;
if (L <= mid) add_jia(ls(x), L, R, k);
if (mid < R) add_jia(rs(x), L, R, k);
pushup(x);
}
int query(int x, int L, int R) {
if (L <= ll[x] && rr[x] <= R) return sum[x];
pushdown(x);
int mid = (ll[x] + rr[x]) >> 1;
int ret = 0;
if (L <= mid) (ret += query(ls(x), L, R)) %= m;
if (mid < R) (ret += query(rs(x), L, R)) %= m;
return ret;
}
signed main() {
cin >> n >> q >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
build(1, 1, n);
while (q--) {
int opt;
cin >> opt;
if (opt == 1) {
int x, y, k;
cin >> x >> y >> k;
add_cheng(1, x, y, k);
} else if (opt == 2) {
int x, y, k;
cin >> x >> y >> k;
add_jia(1, x, y, k);
}
if (opt == 3) {
int x, y;
cin >> x >> y;
cout << query(1, x, y) << '\n';
}
}
return 0;
}
例题3 SP1617:
怎么求解区间最大子段和呢?我们的核心问题是解决\(pushup\)。
首先,如果不跨越中间分界线,左右两边的最大子段和可以直接成为当前区间的最大子段和。
其次,如果跨越了中间分界线,那么左右两边的最大子段和可以直接由左边的最大后缀和和右边的最大前缀和拼起来。
而最大后缀和和最大前缀和也需要\(pushup\),它们的维护是简单的。
代码:
#include <cstdio>
#define max(a, b) ((a) > (b) ? (a) : (b))
#define ls(x) ((x) << 1)
#define rs(x) ((x) << 1 | 1)
typedef long long ll;
const int N = 50001;
int n, q;
struct Node {
ll sum, f, b, ans;
};
struct SegmentTree {
int l, r;
Node dat;
} tr[N << 2];
Node merge(Node a, Node b) {
Node ret;
ret.sum = a.sum + b.sum;
ret.f = max(a.f, a.sum + b.f);
ret.b = max(b.b, b.sum + a.b);
ret.ans = max(max(a.ans, b.ans), a.b + b.f);
return ret;
}
inline void pushUp(int rt) {
tr[rt].dat = merge(tr[ls(rt)].dat, tr[rs(rt)].dat);
return;
}
void build(int rt, int l, int r) {
tr[rt].l = l, tr[rt].r = r;
if (l == r) {
ll inn;
scanf("%lld", &inn);
tr[rt].dat.ans = tr[rt].dat.f = tr[rt].dat.b = tr[rt].dat.sum = inn;
return;
}
int mid = (l + r) >> 1;
build(ls(rt), l, mid);
build(rs(rt), mid + 1, r);
pushUp(rt);
return;
}
Node query(int rt, int ask_l, int ask_r) {
if (ask_l <= tr[rt].l && tr[rt].r <= ask_r) return tr[rt].dat;
int mid = (tr[rt].l + tr[rt].r) >> 1;
Node ret, a, b;
bool flag1 = 0, flag2 = 0;
if (ask_l <= mid) a = query(ls(rt), ask_l, ask_r), flag1 = 1;
if (mid < ask_r) b = query(rs(rt), ask_l, ask_r), flag2 = 1;
if (flag1 && !flag2) return a;
if (!flag1 && flag2) return b;
return merge(a, b);
}
void update(int rt, int x, int k) {
if (tr[rt].l == tr[rt].r && tr[rt].l == x) {
tr[rt].dat.sum = tr[rt].dat.f = tr[rt].dat.ans = tr[rt].dat.b = k;
return;
}
int mid = (tr[rt].l + tr[rt].r) >> 1;
if (x <= mid) update(ls(rt), x, k);
else update(rs(rt), x, k);
pushUp(rt);
return;
}
int main() {
scanf("%d", &n);
build(1, 1, n);
// for (register int i = 1; i <= (n << 1); ++i)
// printf("(%d %d): %lld %lld %lld %lld\n", tr[i].l, tr[i].r, tr[i].dat.sum, tr[i].dat.f, tr[i].dat.b, tr[i].dat.ans);
scanf("%d", &q);
for (int i = 1; i <= q; ++i) {
int opp, xx, yy;
scanf("%d %d %d", &opp, &xx, &yy);
if (opp) printf("%lld\n", query(1, xx, yy).ans);
else update(1, xx, yy);
}
return 0;
}
例题4 P4145:
发现一个很严重的问题:开平方这个操作,完全不能\(pushdown\)。
观察:一个数不会被开很多次平方,\(5\)位数开至多\(4\)次方就变成\(1\)了。
因此我们的策略是:每次修改,看一下这个区间的最大值,如果小于等于\(1\),那么直接不动这个区间。如果大于1,那么直接两边递归下去把它们一个一个改了。
复杂度是\(O(nlognlogV)\)
代码:
#include <cstdio>
#include <algorithm>
#include <cmath>
using std::max;
using std::swap;
using std::sqrt;
typedef long long ll;
#define N 110000
#define ls(x) ((x) << 1)
#define rs(x) ((x) << 1 | 1)
int n, q;
ll a[N];
struct SegmentTree {
int l, r;
ll mx, sum;
} tr[N << 2];
inline void pushUp(int rt) {
tr[rt].mx = max(tr[ls(rt)].mx, tr[rs(rt)].mx);
tr[rt].sum = tr[ls(rt)].sum + tr[rs(rt)].sum;
return;
}
void build(int rt, int l, int r) {
tr[rt].l = l, tr[rt].r = r;
if (l == r) {
tr[rt].mx = tr[rt].sum = a[l];
return;
}
int mid = (l + r) >> 1;
build(ls(rt), l, mid);
build(rs(rt), mid + 1, r);
pushUp(rt);
return;
}
void update(int rt, int ask_l, int ask_r) {
if (ask_l <= tr[rt].l && tr[rt].r <= ask_r && tr[rt].mx <= 1) return;
if (tr[rt].l == tr[rt].r) {
tr[rt].sum = (int)sqrt((double)tr[rt].sum);
tr[rt].mx = (int)sqrt((double)tr[rt].mx);
return;
}
int mid = (tr[rt].l + tr[rt].r) >> 1;
if (ask_l <= mid) update(ls(rt), ask_l, ask_r);
if (mid < ask_r) update(rs(rt), ask_l, ask_r);
pushUp(rt);
return;
}
ll query(int rt, int ask_l, int ask_r) {
if (ask_l <= tr[rt].l && tr[rt].r <= ask_r) {
return tr[rt].sum;
}
int mid = (tr[rt].l + tr[rt].r) >> 1;
ll ans = 0;
if (ask_l <= mid) ans += query(ls(rt), ask_l, ask_r);
if (mid < ask_r) ans += query(rs(rt), ask_l, ask_r);
return ans;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
build(1, 1, n);
// for (register int i = 1; i <= n << 1; ++i) printf("(%d,%d) %d, %d\n", tr[i].l, tr[i].r, tr[i].mn, tr[i].sum); √
scanf("%d", &q);
for (int i = 1; i <= q; ++i) {
int k_, l_, r_;
scanf("%d %d %d", &k_, &l_, &r_);
if (l_ > r_) swap(l_, r_);
if (k_ == 0) update(1, l_, r_);
else printf("%lld\n", query(1, l_, r_));
}
return 0;
}
例题5 P2824:
人类智慧。
二分答案,将整个区间分为小于等于\(mid\)的值记为\(0\),大于\(mid\)的值记为\(1\)。我们希望最后\(mid\)上是\(0\)。
那么排序意味着统计整个区间中\(0\)的数量和\(1\)的数量,然后左边设置为\(0\),右边设置为\(1\)。
这个可以用线段树维护。
代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
const int N = 1e5 + 9;
#define ls ((p) << 1)
#define rs ((p) << 1 | 1)
#define mid (((l) + (r)) >> 1)
int n, m, a[N], qo[N], ql[N], qr[N], c[N];
int tag[N << 2], sum[N << 2];
void pushup(int p) {
sum[p] = sum[ls] + sum[rs];
}
void build(int p, int l, int r) {
tag[p] = -1, sum[p] = 0;
if (l == r) {
sum[p] = a[l];
return ;
}
build(ls, l, mid);
build(rs, mid + 1, r);
pushup(p);
}
void pushdown(int p, int l, int r) {
if (tag[p] != -1) {
tag[ls] = tag[p], tag[rs] = tag[p];
sum[ls] = tag[p] * (mid - l + 1), sum[rs] = tag[p] * (r - mid);
}
tag[p] = -1;
}
void change(int p, int l, int r, int ask_l, int ask_r, int k) {
if (ask_l <= l && r <= ask_r) {
tag[p] = k;
sum[p] = k * (r - l + 1);
return ;
}
pushdown(p, l, r);
if (ask_l <= mid) change(ls, l, mid, ask_l, ask_r, k);
if (mid < ask_r) change(rs, mid + 1, r, ask_l, ask_r, k);
pushup(p);
}
int query(int p, int l, int r, int ask_l, int ask_r) {
if (ask_l <= l && r <= ask_r) return sum[p];
int ret = 0;
pushdown(p, l, r);
if (ask_l <= mid) ret += query(ls, l, mid, ask_l, ask_r);
if (mid < ask_r) ret += query(rs, mid + 1, r, ask_l, ask_r);
return ret;
}
#undef mid
int ask;
bool check(int w) {
// printf("%d\n", w);
for (int i = 1; i <= n; ++i) a[i] = (c[i] >= w);
// puts("");
build(1, 1, n);
for (int i = 1; i <= m; ++i) {
if (qo[i]) {
int num = query(1, 1, n, ql[i], qr[i]);
// printf("%d\n", ql[i] + num - 1);
if (ql[i] + num - 1 >= ql[i])
change(1, 1, n, ql[i], ql[i] + num - 1, 1);
if (ql[i] + num <= qr[i])
change(1, 1, n, ql[i] + num, qr[i], 0);
} else {
int num = qr[i] - ql[i] + 1 - query(1, 1, n, ql[i], qr[i]);
// printf("%d\n", ql[i] + num - 1);
if (ql[i] + num - 1 >= ql[i])
change(1, 1, n, ql[i], ql[i] + num - 1, 0);
if (ql[i] + num <= qr[i])
change(1, 1, n, ql[i] + num, qr[i], 1);
}
// for (int i = 1; i <= n; ++i) printf("%d ", query(1, 1, n, i,i ));
// puts("");
}
int k = query(1, 1, n, ask, ask);
return k;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &c[i]);
for (int i = 1; i <= m; ++i) scanf("%d %d %d", &qo[i], &ql[i], &qr[i]);
scanf("%d", &ask);
int l = 1, r = n, ans = -1, mid;
while (l <= r) {
mid = (l + r) >> 1;
if (check(mid)) ans = mid, l = mid + 1;
else r = mid - 1;
}
printf("%d\n", ans);
return 0;
}
下午
树状数组
树状数组基本上是线段树的弱化但又快又好写版本。
维护一个比线段树更快的数据结构,支持对序列:
\(1.\)单点加
\(2.\)查询前缀和/前缀最大值。
我们魔改一下线段树的结构,删掉每个结点的右儿子。
得到的这个结构仍然保留树的形态,不过我们发现每个位置只会成为唯一一个区间的右端点,因此我们实际上只有线性的\(n\)个区间。
因此我们管这种数据结构叫做“树状数组”。
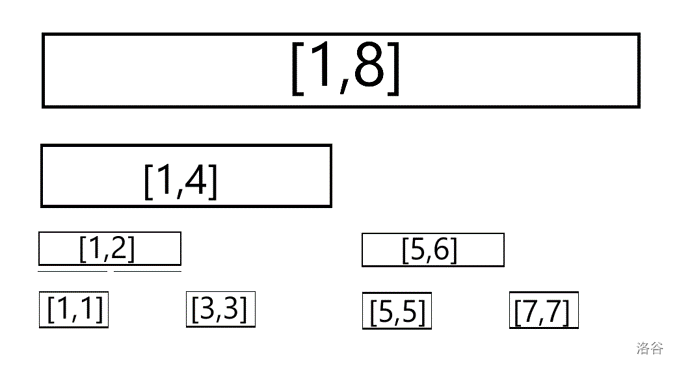
回忆\(lowbit\)
观察:如果我们记\(lowbit(x)\)表示数\(x\)二进制表示从右往前最低位的\(1\)与它之前的所有\(0\)构成的数,例如\(x = (101100)_2,\)那么\(lowbit(x)=(100)_2\)。
利用二进制补码的性质,我们可以得到
lowbit(x)=x&(-x)
我们发现,树状数组的位置\(i\)刚好维护了\((i-lowbit(i),i]\)这个长度为\(lowbit(i)\)的区间。
因此我们只需要一个\(for\)循环就可以轻松维护出树状数组。
例题1 P3374
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e5+10;
#define int long long
inline int lowbit(int x){
return x&(-x);
}
int n,m;
int sum[maxn];//sum[i]代表以i为右端点的那个区间的和
int query(int x){
int ans=0;
for(;x;x-=lowbit(x)){
ans+=sum[x];
}
return ans;
}
void add(int x,int k){
for(;x<=n;x+=lowbit(x))sum[x]+=k;
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
int x;
cin>>x;
add(i,x);
}
while(m--){
int opt;
cin>>opt;
if(opt==1){
int x,k;
cin>>x>>k;
add(x,k);
}
if(opt==2){
int x,y;
cin>>x>>y;
cout<<query(y)-query(x-1)<<endl;
}
}
return 0;
}
例题 P3368:
普通的树状数组是单点加询问前缀和。
这个是区间加询问单点值。
只需要作一个差分就可以在这两个东西之间转化了。
代码:
#include<bits/stdc++.h>
#define lowbit(x) x&(-x)
#define int long long
const int MAXN=5e5+5;
int a[MAXN],b[MAXN];
void modify(int l,int r,int c){
for(int i=l;i<=MAXN;i+=lowbit(i)) b[i]+=c;
for(int i=r+1;i<=MAXN;i+=lowbit(i)) b[i]-=c;
}
int query(int x){
int ans=0;
for(int i=x;i;i-=lowbit(i)) ans+=b[i];
return ans;
}
using namespace std;
signed main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
modify(i,i,a[i]);
}
while(m--){
int caozuo;
cin>>caozuo;
if(caozuo==1){
int l,r,c;
cin>>l>>r>>c;
modify(l,r,c);
}
else{
int x;
cin>>x;
cout<<query(x)<<'\n';
}
}
return 0;
}
二叉搜索树
维护一个数据结构,它是一个集合,支持:
-
加入一个数\((insert)\)
-
删除一个数\((delete)\)
-
查询一个数的排名\((rank,即比它小的数个数+1)\)
-
查询第\(k\)小数\((kth,即从小到大排序后第k个位置上的数)\)
-
查询一个数的前驱\((pre)\)
-
查询一个数的后继\((suc)\)
你只需要一个平均复杂度\(O(logn)\)的算法,不需要保证最坏复杂度。
我们依然使用一棵二叉树去维护这个集合。
这棵二叉树需要满足:一个结点的权值,大于它左儿子的权值,小于它右儿子的权值,如果有相同权值,那么在这个结点的\(count[]上+1\)。
那么这个二叉树看上去就像是把一个排好序的数组“提起来”(换句话说,这个二叉树的中序遍历有序)
那么它为什么叫做“二叉搜索树”呢,因为这棵树可以非常方便地替我们完成“搜素一个值”这个任务。
从树根出发, 每次检查这个值与当前结点的权值的大小关系,如果相等那么找到了,否则如果值比当前结点小,那么向左走,不然向右走。复杂度\(O(树高)\)。
接下来我们开始分别实现这6个功能:
-
插入,从根开始,如果能搜素到这个值那么直接\(count[]++\),不然在搜素到的那个空位置新建一个结点存放这个值。
-
删除,我们最好使用惰性删除,也就是把这个点删了但是这个空点还留在树上。
-
查询一个数的排名,我们在二叉搜索树上查找这个数,如果下一步递归到右儿子,那么将排名增加\(sz[左儿子]+count[当前点]\),最后如果找到了,还需要加上\(sz[左儿子]+1\)。
-
查询第\(k\)小,我们同样在二叉搜索树上从根开始搜素,不过这次变成了:从根开始,如果\(k <= sz[左儿子]\),那么向左儿子递归。如果\(0<k-sz[左儿子]<=count[当前点]\),那么当前点就是答案,否则把\(k\)减去\(sz[左儿子]+count[当前点]\),然后向右递归。
-
查询前驱,其实就是\(kth(rank(v)-1)\)
-
查询后继,其实就是\(kth(rank(v+1))\)
代码:
#include <bits/stdc++.h>
// using std::cin;
// using std::cout;
namespace FastIO {
template<class T> inline void read(T &x) {
x = 0; bool f = 0; int ch = getchar();
for (; !isdigit(ch); f = (ch == '-'), ch = getchar()) ;
for (; isdigit(ch); x = x * 10 + ch - '0', ch = getchar()) ;
x = f ? -x : x;
}
inline int read() {
int x = 0; bool f = 0; int ch = getchar();
for (; !isdigit(ch); f = (ch == '-'), ch = getchar()) ;
for (; isdigit(ch); x = x * 10 + ch - 48, ch = getchar()) ;
return f ? -x : x;
}
int NUM[65];
template<class T> inline void Write(T x) {
if (x == 0) { putchar('0'); return ;}
if (x < 0) putchar('-');
x = x > 0 ? x : -x;
int tot = 0;
while (x) NUM[tot++] = x % 10 + 48, x /= 10;
while (tot) putchar(NUM[--tot]);
}
template<class T> inline void write(T x, char op) {
printf("%d\n", x);
}
}
using namespace FastIO;
const int MAX_N = 1e5;
int n;
int tot = 1;
int rt = 1, ch[MAX_N + 9][2], val[MAX_N + 9], sz[MAX_N + 9], cnt[MAX_N + 9];
void insert(int x) {
int u = rt, lst = 0;
for (; u && val[u] != x; lst = u, u = ch[u][x > val[u]]) sz[u]++;
if (val[u] == x) cnt[u]++, sz[u]++;
else {
if (lst) u = ch[lst][x > val[lst]] = ++tot;
val[u] = x;
cnt[u] = sz[u] = 1;
}
}
int rank(int x) {
int u = rt, res = 0;
for (; u && val[u] != x; u = ch[u][x > val[u]])
if (x > val[u]) res += sz[ch[u][0]] + cnt[u];
if (val[u] == x) res += sz[ch[u][0]];
return res + 1;
}
int kth(int k) {
int u = rt;
while (1) {
if (k <= sz[ch[u][0]]) u = ch[u][0];
else if (k <= sz[ch[u][0]] + cnt[u]) return val[u];
else k -= sz[ch[u][0]] + cnt[u], u = ch[u][1];
}
}
int pre(int x) {
return kth(rank(x) - 1);
}
int suc(int x) {
return kth(rank(x + 1));
}
void del(int x) {
int u = rt, lst = 0;
for (; val[u] != x; lst = u, u = ch[u][x > val[u]]) sz[u]--;
cnt[u]--, sz[u]--;
}
int main() {
read(n);
while (n--) {
int op = read(), x = read();
switch (op) {
case 1 : insert(x); break;
case 2 : del(x); break;
case 3 : write(rank(x), '\n'); break;
case 4 : write(kth(x), '\n'); break;
case 5 : write(pre(x), '\n'); break;
case 6 : write(suc(x), '\n'); break;
default : break;
}
}
return 0;
}
二叉搜索树和线段树
其实二叉搜索树可以看成某种意义上的线段树,这意味着它可以承担一些区间操作的任务,也可以打懒标记。(比如\(splay\)和\(fhqtreap\)可以做的区间\(reverse\))
同理,线段树也可以视作一种二叉搜索树,这让它也可以维护一个集合。(动态开点权值线段树)
二叉搜索树最坏时间复杂度显然是\(O(n)\)的,其原因在于这棵搜索树可以长得很不“平衡”,(最平衡的二叉树就是完全二叉树)
因此我们想出了各种奇奇怪怪的方法让二叉搜索树保持平衡,来让它能够真正达到\(O(logn)\)的时间复杂度。
这里给大家介绍一个非常简单但不是很实用的平衡树:替罪羊树。
它的思路很简单暴力:我们不平衡,那么我们每当整棵树不平衡到一个程度了,就把它整个推平重构成一棵完全二叉树。
这个所谓“不平衡到一个程度”,我们认为:其左或右儿子的大小\(>\)整个子树大小的\(0.7\)倍,或者删除的点的数量占整棵树的\((1 – 0.7=0.3)\)倍。
因为这个操作支持删除不是很容易,因此我们直接采用懒惰的方法,如果一个结点的\(count\)为\(0\)就把它留在那里不动它。
可以通过一些深刻的复杂度证明它的复杂度是\(O(nlogn)\)的。
字符串
字符串当然就是由若干字符拼成的串。
关于字符串,我们讨论的其中一个就是字符串的“匹配”问题,也就是说,我给出两个字符串,你怎么知道其中一个串是另一个串的子串?它在多少地方出现了?这也是我们本次课研究的问题。其它的问题,我们会放到今后学习各种子串科技(后缀数组,后缀自动机,基本子串结构)的时候。
概念:
\(1.\) 字符集:就是字符串里所有字符构成的集合。
$2. $子串:就是字符串的一个区间。
\(3.\) 前缀/后缀:就是字符串一个从\(1\)开始的区间和一个以\(n\)结尾的区间。
哈希
什么是哈希?哈希是一种容易被卡的算法。
哈希是一种不能保证正确性的算法,但是这不代表你使用哈希会被随机扣分。
它的运作思路是:我们把一个字符串不一一对应地对应到一个数上,然后比较这两个数就可以得到这两个字符串的关系了。
字符串哈希
我们使用这样一种哈希方法:
将整个字符串视为一个\(b\)进制的数字对一个大质数\(p\)取模得到的数字。
譬如,对于字符串\(s=“abc”\),这种哈希值对应的结果就是\(1+2×𝑏+3×𝑏^2\)。
其中\(b\)和\(p\)的值可以随便取,一般\(b\)取\(29\)或者\(31\),\(p\)取\(1e9+7\)或者\(998244353\)。
那么,两个相同字符串的哈希值显然是相同的。
更进一步地,我们可以轻松地求出这个字符串所有子串的哈希值。
代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 9;
const int b1 = 29, p1 = 1e9 + 7;
const int b2 = 31, p2 = 998244353;
char s[maxn];
int hsh1[maxn], base1[maxn];
int hsh2[maxn], base2[maxn];
int getHash1(int l, int r) {
return (hsh1[r] - 1ll * hsh1[l - 1] * base1[r - l + 1] % p1 + p1) % p1;
}
int getHash2(int l, int r) {
return (hsh2[r] - 1ll * hsh2[l - 1] * base2[r - l + 1] % p2 + p2) % p2;
}
int main() {
scanf("%s", s + 1);
int n = strlen(s + 1);
base1[0] = 1;
for (int i = 1; i <= n; i++)
base1[i] = 1ll * base1[i - 1] * b1 % p1;
base2[0] = 1;
for (int i = 1; i <= n; i++)
base2[i] = 1ll * base2[i - 1] * b2 % p2;
for (int i = 1; i <= n; i++) {
hsh1[i] = (1ll * hsh1[i - 1] * b1 % p1 + (s[i] - 'a' + 1)) % p1;
}
for (int i = 1; i <= n; i++) {
hsh2[i] = (1ll * hsh2[i - 1] * b2 % p2 + (s[i] - 'a' + 1)) % p2;
}
int l1, r1, l2, r2;
cin >> l1 >> r1 >> l2 >> r2;
if (getHash1(l1, r1) == getHash1(l2, r2) && getHash2(l1, r1) == getHash2(l2, r2))
puts("Yes");
else
puts("No");
return 0;
}
哈希冲突
一个\(100000\)长度的字符串,子串的个数将近\(1e10\),可是你的模数只有\(1e9\),这就意味着这个字符串几乎一定会出现两个不同的子串具有相同的哈希值,那么如果你比较这两个子串,就会得到错误的结果,也就是我们所说的“哈希冲突”。
某种意义上,哈希冲突是无法规避的。然而,这种冲突发生的概率非常微小(你不可能把所有\(1e10\)个子串两两比较)。因此,我们期望它不会在自然状态下出现这种情况。
如果你不想让\(OI\)比赛的出题人人为地卡掉你的哈希,那么一个办法是使用不太常见的模数(比如\(1e9+33\)),不过通常不会有毒瘤出题人会专门设计卡某一个特定哈希值的数据。(如果你遇到了,请狠狠攻击)
不过,一个更保险的方法是使用双值哈希。顾名思义,就是同时用两套b和p去计算哈希值,这样相当于有了一个双重保险。就几乎不可能出错了,被卡也很难。
哈希表
维护一个数据结构,是一个集合,支持:
-
插入一个\((key,value)\)对
-
删除一个\((key,value)\)对
-
查询一个\(key\)对应的数是什么。
要求总共接近\(O(n)\)地做完这些事情。
我们采取一个极端措施:给插入的值对一个\(1e6\)左右的数取模\((1e6-3)\)。把得到的数当作\(vis[]\)的数组下标。
但是因为这个数很小,所以很容易出现哈希冲突,怎么办呢?
答案是把这个\(vis[]\)数组拓展成一个链表。每次插入一个数,如果发现这个数与其它的数哈希冲突了,就把它挂在先前的这个数后面。
这样就可以做到一个几乎线性的查询复杂度,显著优于同台竞争的线段树和平衡树。
代码:
#define ll long long
const int maxm=3e6+9,maxt=2e6+9;
const ll p1 = 1145141, p2 = 1e9 + 7, p3 = 998244353, base = 131;
struct HashMap {
int tot;
int head[maxm], nxt[maxt];
ll hsh1[maxt], hsh2[maxt];
void insert(ll x, ll y) { // hsh1 = x , hsh2 = y
int v = x % p1;
hsh1[++tot] = x, hsh2[tot] = y, nxt[tot] = head[v], head[v] = tot;
}
bool query(ll x, ll y) { // 查询 x y 这个哈希值是否在哈希表中出现过
int v = x % p1;
for (int i = head[v]; i; i = nxt[i]) {
if (hsh1[i] == x && hsh2[i] == y) return 1; // 找到了
}
return 0; // 没找到
}
} ht;
例题1 P7469:
枚举\(B\)剩下的子串的左端点\(l\),考虑让\(r\)从\(l\)到\(n\)逐步扩展右端点。
那么我们只需要在\(A\)串上,首先找到第一个为\(b[l]\)的位置,然后再从\(b[l]\)开始找它的下一个第一个为\(b[l+1]\)的位置,以此类推,如果有一个位置匹配不上就让\(l++\)。找下一个\(b[]\)的过程可以维护一个\(c[i][j]\)表示从点\(i\)开始的第一个字母\(j\)在哪个位置。然后在预处理的时候从后往前扫一遍\(A\)串得到答案。
现在的问题是如何统计答案。由于字符串不能重复,我们需要每次将字符串的哈希值存下来,每次检查它与先前的哈希值是否相同。因此我们需要一个哈希表来完成这个事情。
代码:
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <ctime>
#include <algorithm>
#include <bitset>
#include <complex>
#include <deque>
#include <iomanip>
#include <iostream>
#include <iterator>
#include <list>
#include <map>
#include <memory>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <vector>
#define DEBUG
#define debug(x) printf("%s = %d\n", #x, x);
#define outputArray(x, n) for (int OPA = 1; OPA <= (n); ++OPA) printf("%d ", x[OPA]); puts("");
typedef long long ll;
using std::swap;
using std::reverse;
using std::priority_queue;
using std::nth_element;
using std::next_permutation;
using std::upper_bound;
using std::lower_bound;
using std::unique;
using std::sort;
using std::max;
using std::min;
using std::cin;
using std::cout;
using std::endl;
using std::string;
using std::bitset;
using std::set;
using std::map;
using std::vector;
using std::queue;
using std::stack;
using std::pair;
using std::make_pair;
using std::complex;
using std::deque;
using std::list;
int read() {
register int x = 0, f = 0, ch = getchar();
for (; !isdigit(ch); f = (ch == 45), ch = getchar()) ;
for (; isdigit(ch); x = x * 10 + ch - 48, ch = getchar()) ;
return f ? -x : x;
}
void write(int x) {
if (x < 0) putchar(45), x = -x;
static int sta[35];
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
while (top) putchar(sta[--top] + 48);
}
const int maxn = 3e3 + 9, maxm = 2e6 + 9, maxt = 9e6 + 9;
const ll p1 = 1145141, p2 = 1e9 + 7, p3 = 998244353, base = 131;
int n, m, a[maxn], b[maxn];
char s[maxn];
int pos[maxn], nxt[maxn][31];
struct HashMap {
int tot;
int head[maxm], nxt[maxt];
ll hsh1[maxt], hsh2[maxt];
void insert(ll x, ll y) {
int v = x % p1;
hsh1[++tot] = x, hsh2[tot] = y, nxt[tot] = head[v], head[v] = tot;
}
bool query(ll x, ll y) {
int v = x % p1;
for (int i = head[v]; i; i = nxt[i]) {
if (hsh1[i] == x && hsh2[i] == y) return 1;
}
return 0;
}
} ht;
int main() {
// freopen(".in", "r", stdin);
// freopen(".out", "w", stdout);
n = read();
scanf("%s", s + 1); for (int i = 1; i <= n; ++i) a[i] = s[i] - 'a' + 1;
scanf("%s", s + 1); for (int i = 1; i <= n; ++i) b[i] = s[i] - 'a' + 1;
for (int i = 1; i <= 26; ++i) pos[i] = n + 1;
for (int i = n; i; --i) {
for (int j = 1; j <= 26; ++j) nxt[i][j] = pos[j];
pos[a[i]] = i;
}
ll hsh1 = 0, hsh2 = 0;
int ans = 0;
for (int i = 1; i <= n; ++i) {// 枚举B的左端点i
hsh1 = hsh2 = 0;
for (int j = i, k = pos[b[j]]; k != n + 1 && j <= n; ++j, k = nxt[k][b[j]]) {
// j 是 B的右端点 , k 初值, b[j]第一次出现的位置 pos[b[j]]
hsh1 = (hsh1 * base % p2 + b[j]) % p2, hsh2 = (hsh2 * base % p3 + b[j]) % p3;
if (!ht.query(hsh1, hsh2)) ht.insert(hsh1, hsh2), ++ans;
}
}
printf("%d\n", ans);
return 0;
}
TRIE 树:
我们现在有很多字符串,怎么判断哪些字符串出现过,哪些字符串没有出现过呢?
我们考虑一本字典,如果我们想要在一个字典中找到某个单词,我们的做法是:首先找它的第一个字母,翻到指定页数后开始找第二个字母,如法炮制。
发现这个过程很像一棵树,因此我们可以模仿这个过程建一棵树,我们称为trie树。
显而易见地,对于一个小写字母字符集而言,trie树的每个结点需要一个\(ch_{i,26}\)来存储它的26个儿子,但是无论是插入还是查找都是\(O(len)\)的。
上面那个题其实给了我们一个提示:trie不仅仅可以用来存储字符串,也可以用二进制的形式存储数!
因此我们瞬间得到了一个树高log值域的二叉搜索树!(当然,与一般的二叉搜索树略有不同)
Trie瞬间就变得非常厉害了!
唯一的不足是花费的空间和时间是同阶的,都是O(nlogV),但是常数要比平衡树优秀很多,可以作为一个低配的平衡树使用。
01TRie:
上面那个题其实给了我们一个提示:trie不仅仅可以用来存储字符串,也可以用二进制的形式存储数!
因此我们瞬间得到了一个树高 \(log\) 值域的二叉搜索树!(当然,与一般的二叉搜索树略有不同)
Trie瞬间就变得非常厉害了!
唯一的不足是花费的空间和时间是同阶的,都是 \(O(nlogV)\),但是常数要比平衡树优秀很多,可以作为一个低配的平衡树使用。
KMP:
给定长一点的字符串 \(S\)(称为文本串)和短一点的字符串 \(T\)(称为模式串),求 \(T\) 在 \(S\) 中的哪些位置出现(找T出现位置的开头位置)
要求 \(O(|S|+|T|)\)
不能使用哈希。
我们枚举 \(T\) 在 \(S\) 上的起点 \(i\),然后用 \(j\) 一位一位地匹配。发现 \(j=6\) 的时候寄掉了。此时我们需要从 \(i=2\) 再重新匹配吗?并不需要。我们匹配了子串 \(T[1,5]\),那么下一个有可能成为 \(T\) 匹配位置的起点会长成这样。
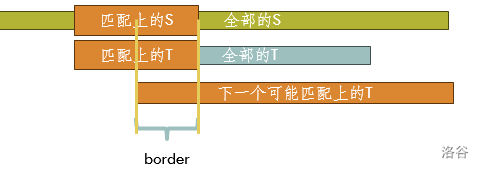
所以问题就很显然了。我们下一步并不需要从头开始,而只需要从 \(T\) 的 \(border\) 位置开始即可。
那么我们的算法流程是:失配->跳border->再失配->再跳border。
这样,我们每次在 \(S\) 上移动一步,在 \(T\) 上也移动了一步,border最多增加 \(1\),于是我们最多只会增加 \(|S|\) 次border,那么自然也最多回跳小于 \(|S|\) 次border,复杂度于是就是 \(O(|S|+|T|)\)。
因为这个跳border的操作有点像指示失配之后“下一个”位置在哪的数组,因此有人用 \(nxt\) 数组表示border。
code:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 9;
char s1[maxn], s2[maxn];
int nxt[maxn];
int main() {
scanf("%s", s1 + 1);
scanf("%s", s2 + 1);
int n = strlen(s1 + 1), m = strlen(s2 + 1);
nxt[1] = 0;
for (int i = 2, j = 0; i <= m; i++) {
while (j && s2[j + 1] != s2[i]) j = nxt[j];
if (s2[j + 1] == s2[i]) ++j;
nxt[i] = j;
}
for (int i = 1, j = 0; i <= n; i++) {
while (j && s2[j + 1] != s1[i]) j = nxt[j];
if (s2[j + 1] == s1[i]) ++j;
if (j == m) {
printf("%d\n", i - m + 1);
j = nxt[j];
}
}
for (int i = 1; i <= m; i++) printf("%d ", nxt[i]);
puts("");
return 0;
}
STL:
模板:template
实际上这个东西是C++的一个语法,它的作用类似于我们学过的“通配符”,可以检测任何一种类型,甚至是你自己定义的struct。
比如,std::queue的实现是这样的。
你不用管那些吓人的语法,我们将
重点落在这里。
这就是我们的那个类型名的位置。
这个template决定了STL是相当泛用的。
容器container
容器就是STL里的数据结构,是拿来存放数据的瓶瓶罐罐。
容器分为序列容器(vector,list,deque),关联容器(set,map)和其它容器(bitset)。
你可以简单理解为,数组,平衡树,和bitset。
它们是一个个的class(你可以把它们当作struct来用),怎么用?
\(std::vector<int> vec;\)
从左到右分别是命名空间(standard),容器名,模板参数,变量名。
然后你就获得了一个名叫 \(vec\) 的,里面存放 \(int\) 类型的 \(vector\) 容器。
迭代器 iterator
迭代器像是 \(STL\) 版本的指针,用来在容器的各个元素之间移动。
首先,我们造一个iterator,
\(std::vector<int>::iterator it;\)
这一行从 \(std::vector<int>\) 这个类中找出它里面的一个类iterator,用它定义了一个变量it。
那么这个 \(it\) 就可以在 \(vector\) 上乱转了,比如
$ for (it = vec.begin(); it != vec.end(); it++)$ …
如果想要访问 \(iterator\) 指向的值,就需要使用*it。
vector
向量 \(vector\),你可以把它当成一个可以延长的数组。它的延长方式是,每次将自己的存储空间加倍。
它支持:
1.用下标访问一个位置,\(vec[1],O(1)\)。
2.在末尾删除或插入元素,\(ec.push_back(1),O(1)\)。
3.插入或删除一个元素:与到 \(vector\) 结尾的距离成线性\(O(n)\)。\(vec.clear()\),清空 \(vector\) 但不清空内存。
4.\(vec.empty()\), 返回一个 \(bool\) 代表 \(vector\) 是否为空
5.\(vec.size()\),返回一个 \(unsigned int\) 代表 \(vector\) 的元素个数。
6\(.vec.begin(), vec.end()\),返回一个迭代器代表 \(vector\) 的第一个位置与【最后一个位置的下一个位置】。
7.\(vector.front(),vec.back()\),返回 \(vector\) 的第一个元素和最后一个元素。
8.\(vec.front(),vec.back()\),返回 \(vector\) 的第一个元素和最后一个元素。
9.\(vec.insert(it, val)\); 在迭代器 \(it\) 前插入值 \(val\)。插入后仅被插入点前的迭代器有效。返回这次插入/删除得到的迭代器。
10.\(vec.resize(n)\); 将 \(vector\) 大小设为 \(n\),多余的直接扔掉,复杂度与原大小的差线性。
11.\(vec.erase(it)\);删除迭代器所指的元素,其余同\(insert\)。
12.\(vec.reserve(n)\);将 \(vector\) 的存储空间设为 \(n\),不改变其大小,不能用来减少存储空间。
13.\(std::vector<int> vec(n)\); 生成一个初始大小为 \(n\) 的\(vector\),全是0.
14.\(std::vector<int> vec(n,val)\); 生成一个初始大小为 \(n\) 的 \(vector\),全是 \(val\)。
15.\(std::vector<int> vec = {1, 2, 3, 4}\); 生成一个初始元素为 \({1,2,3,4}\) 的 \(vector\).
16.$for (int v : vec) {} $顺序遍历 $vec $的每一个元素。
string:
\(std::string\) 是C++风格的字符串,它几乎就是一个\(std::vector<char>\),具有 \(vector\) 的上述所有功能。
- \(s.append(6,’*’)\); 向 \(s\) 末尾添加 \(6\) ’’,返回this。
2 \(s.append(str), s.append(str,n\)),向 \(s\) 末尾添加 \(C\) 风格字符串 \(str\),str的前 \(n\) 个字符,如果 \(str\) 是另一个 \(std::string\) ,后者代表从位置 \(n\) 开始 \(append\)。
3.用+和+=连接字符串。
4.\(s.substr(pos, count)\) 返回 \([pos,pos+count)\) 这一段子串,不输入 \(count\) 就是到最后。
5.\(std::stoi(s)\); 把 \(s\) 变成一个 \(int\) 类型的数,类似的还有 \(std::stoll,std::stod\)。
6.\(std::to_string(x)\):把 \(x\) 变成一个字符串,支持 \(int,longlong,double\) 等。
queue
\(queue\) 是我们常说的FIFO的队列。
它仅仅支持\(front(),back(),empty(),size()\)这种简单的功能。
还有\(push(x),pop()\),分别表示向队尾插入元素,向队头删除元素。
不支持迭代器。
stack:
\(stack\) 是我们常说的FILO的栈。
它支持\(empty(),size(),push(),pop()\)这种显而易见的功能。
它还支持\(top()\),访问栈顶元素。
deque:
\(deque\) 算是一个加强版的 \(vector\) ,支持向头尾插入/删除元素,并且这玩意访问下标的效率居然是 \(O(1)\) 的!(有点常数)
支持\(empty(),front(),front(), back(), begin(),end(),clear(),insert(),erase(),push_back(),push_front(),pop_back(),pop_front(),resize()\)这些和\(vector\) 一样的东西。
\(queue\) 和 \(stack\) 是通过 \(deque\) 实现的。
另:在NOI2022中,有若干名选手在比赛中使用了1e6个deque,由于deque会在创建时分配4个int的内存,因此造成了MLE,DayT1获得了0分。
set:
集合 \(set\) 是一个功能很少的平衡树,功能基本都是 \(logn\) 的,但是因为STL封装的特性,速度不及手写,开了O2跑得还行,常用。
-
$std::set
s; $声明一个名为 \(s\) 的set. -
\(s.insert(s); s.erase(s)\); 将s加入集合,剔除集合。注意集合具有互异性,两个相等的元素会被视为一个。
-
set支持\(begin(), end()\),它的迭代器左右移动是按照值从小到大的顺序遍历每一个结点的,换句话说每次++it,它都会找到这个迭代器的后继结点。
-
\(s.lower_bound(x)\);返回第一个值不小于x的元素对应的迭代器,相当于二分。
-
\(s.upper_bound(x)\);分会第一个值大于x的元素对应的迭代器。
-
\(s.count(x)\); 返回元素x的数量,只可能为0或1.
7.$ s.find(x)$; 返回元素x对应的迭代器,如果没有返回s.end();
8.$ clear(), size(), empty()$,无需多言。
map:
映射 \(map\) 在底层的实现其实几乎和 \(set\) 是一样的,大家可以把它当成一个下标不一定是非负整数的数组。它的实现原理是用 \(set\) 存 \(pair\)。
-
\(map<int, double> mp\); 声明一个存储着从 \(int\) 到\(double\) 的映射。
-
\(mp[2] = 3.3\); 将 \(mp\) 中 \(2\) 对应的 \(double\) 改为 \(3.3\),如果先前 \(2\) 没有对应的数,那么新建一个 \(2 -> 3.3\) 的对应关系。
-
\(mp.count(x)\); 返回有 \(x\) 这个键值的 \(pair\) 有几个。(0或1)
-
\(mp.insert(make_pair(1,2))\); 向 \(mp\) 中插入一个 \(1->2\) 的对应关系,如果先前已经有 \(1\) 的对应关系,这次插入失败。
-
\(clear(), size(), empty()\),无需多言。
multiset/multimap:
可重集合/可重映射。
顾名思义,就是在 \(set\) 和 \(map\) 的基础上,每个元素可以出现多次。
注意,\(multiset\) 和 \(multimap\) 的 \(erase\) 会杀掉所有与这个值相等的元素。如果只想杀掉一个,使用 \(find\) 函数找到任意一个该元素的迭代器 \(it\)后,\(s.erase(it)\);
unordered_map:
C++内置的哈希表。
与 \(map\) 用法基本相同。
不推荐使用,建议手写。
bitset:
顾名思义,存储bit的定长数组。
1.声明一个 \(bitset<8> b\) ; 可以给它赋初值,例如\(bitset<8> b(42);\)
\ \(b = 00101010\)
\(bitset<4> b(“0011”); \\ b = 0011\)
-
\(bitset\) 就像是一个很长很长的二进制数,它可以与其它二进制数或者 \(bitset\) 进行位运算。
-
可以用[]访问其特定某一位。
-
\(.all(), .any(), .none()\) 表示是否所有位/存在位/没有位被设为 \(1\)。
-
\(.count()\) 返回 \(1\) 的个数。
-
\(size()\) 返回大小,即 \(bitset<n> b\); 的那个 \(n\)
-
$.set() $设置所有位为\(1\),\(set(p)\) 将位置 \(p\) 设为 \(1\), .\(set(p, x)\) 将位置 \(p\) 设为\(x\) ,.\(reset()\) 清空 \(bitset\),. \(reset(p)\) 将位置 \(p\) 设为 \(0\)。\(.flip()\)将所有位异或 \(1\),.\(flip(p)\) 将位置 \(p\) 异或 \(1\).
-
.\(to_string(char zero = ‘0’, char one = ‘1’)\),返回一个\(std::string\),将\(bitset\)的值转换为一个字符串,其中\(0\)的位置用变量\(zero\)替换,\(1\)的位置用变量 \(one\) 替换。
-
\(.to_ulong(); .to_ullong();\) 将值转换为 \(unsigned long\) 或者 \(unsigned long long\),如果不能转换会报错。
bitset的妙用:
\(bitset\)所有操作的复杂度是\(O(n/w)\)的,其中\(w=32\),也就是说\(bitset\)实际上做到了把一个 \(int\),\(4\) 个字节,\(32\) 个 \(bit\) 的信息同时处理,因此可以加速某些运算。
另一方面,\(bitset\) 因为是有压位,其连续读写效率相当优秀,利用它代替 \(bool\) 数组有时候也能起到加速的作用。例如,大家都学过用埃氏筛法筛质数。利用 \(bitset\) 优化后埃氏筛法的速度要快于欧拉筛。(见oi-wiki)
std::swap:
交换两个对象,可以是变量,可以是容器。
std::max/std::min:
传入两个数 \(a,b\),返回它们中较大的那一个/较小的那一个。
一般使用方法:\(std::max(1, 2), std::min(a,b)\);
特殊使用方法:\(max({1,2,3,4,5});\)
std::sort:
将一列数排序。
-
\(sort(a + 1, a + n + 1, cmp)\); 将一个数组 \(a[1,n]\) 排序,\(cmp\) 是一个函数的名字,代表排序方式,
-
bool cmp(int a, int b) { return a < b; } 这个是从小到大排序,小于号改成大于号是从大到小排序,不要写成小于等于和大于等于。
-
\(sort\) 还可以对 \(vector\) 排序,方法是\(sort(vec.begin(), vec.end(), cmp);\)
复杂度 \(O(nlogn)\)。
std::unique:
将一个序列相邻的元素去重,把重复元素扔到末尾,返回去重后数组的末尾位置的下一个位置的指针。
通常用法:\(sort(a+1, a+n+1); n=unique(a+1,a+n+1)-a-1;\)
对 \(vector\) 去重:\(vec.erase(unique(vec.begin(),vec.end()), vec.end());\)
复杂度 \(O(n)\)。
std::reverse:
顾名思义,将一个序列头尾整个翻转。
比如把 \(1 2 3 4 5\) 反转为 \(5 4 3 2 1\).
可以翻转数组,vector,字符串。
复杂度 \(O(n)\)。
std::find:
顺序查找值,返回指向这个值的指针/迭代器,返回第一个位置。
一般用法 \(int p = find(a+1,a+n+1,114) – a;\)
lower_bound:
对一个已经单调不降的序列进行二分,返回指向第一个大于等于 \(x\) 的位置的指针。
一般用法 \(int p = lowerbound(a+1,a+n+1,514) – a;\)
\(upperbound\) 同理,之前已经讲过。
next_permutation:
给定一个排列,生成这个排列的下一个排列。
一般用法:枚举全排列用来打暴力:
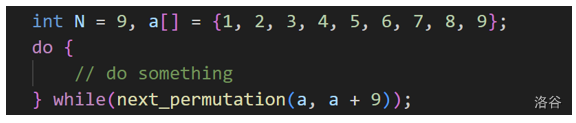
nth-element:
找出序列中第 \(n\) 小的元素,然后重排整个序列,使其左边均为比它小的数,右边均为比它大的数。复杂度几乎是 \(O(n)\) 的。
一般用法:\(nth_element(a+1,a+k, a+n+1,cmp);\)
代表找出序列中第 \(k\) 小的元素。
晚上
王铭宇老师讲的非常好,今天是他最后一天讲课,这里引用了他整理的三天的总题单,感谢老师orz!
posted on 2025-01-26 08:09 zhaohaocheng1234 阅读(7) 评论(0) 收藏 举报

 浙公网安备 33010602011771号
浙公网安备 33010602011771号