2023 年 10 月训练记录

训练记录

10 月了。

CF457F An easy problem about trees

尝试理解，感谢 cz_xuyixuan 的题解。

算作是很多情况的补充说明。

我们不妨先二分答案，将 \(\ge mid\) 的设为 \(1\)，\(<mid\) 的设为 \(0\)，于是问题转化为了权值均为 \(0/1\) 的版本。

我们称一棵树的大小为其非叶节点数。

我们称一棵大小为奇数的树为奇树，大小为偶数的树为偶树。

对于奇树有两棵偶子树的情况：最后一次操作由先手完成。我们称，先手能够在当前子树内获胜当且仅当他能在任意一棵子树作为先手内获胜。这是因为如果先手可以在任意一棵子树内获胜，他就可以采取模仿的策略：先在他能赢的子树内操作，如果后手去操作了别的子树，则先手也同样去另一棵子树操作。反之，后手也可以用同样的策略，使得先手在两棵子树内都无法获胜。

对于奇树有两棵奇子树的情况：注意到一棵子树被操作完后，另一棵子树的先后手会发生变化，所以情况就变得更加复杂了，不能单纯地模仿。我们观察其中一棵子树就会发现操作的形式相当于跳过了一次自己的回合，先后手都有这样的机会。

可以发现的是，多次跳过回合是没有意义的，因为对方玩家同样可能进行跳过，而使我方上次的跳过失效，因此，只需要记录是否可以跳过的回合。

于是我们增设状态 \(skip\)：

\(=0\)：不能 \(skip\)；
\(=1\)：可以 \(skip\)；
\(=2\)：先手可以 \(skip\)，若先手不 \(skip\)，后手必须 \(skip\)，详见后文。

于是，我们分情况讨论：

\(skip=0\)：
1. 奇树有两棵偶子树：先手能获胜当且仅当在任意一个子树内的 \(skip=0\) 能获胜；
2. 奇树有两棵奇子树：先手能获胜当且仅当在任意一个子树内的 \(skip=1\) 能获胜；
3. 偶树：显然有一个奇子树和一个偶子树。我们不妨枚举先手的第一步操作：
  1. 操作奇树，那么对于后手相当于情况 1.1。所以，先手能获胜当且仅当先手能奇树中 \(skip=0\) 获胜，并且后手不能在偶树中 \(skip=0\) 获胜；
  2. 操作偶树，那么对于后手相当于情况 1.2。所以，先手能获胜当且仅当先手能偶树中 \(skip=1\) 获胜，并且后手不能在奇树中 \(skip=1\) 获胜。
  先手可以选择操作。
\(skip=1\)：

先手首先可以考虑 \(skip\)，若后手不能在剩余局面中获胜，则先手获胜。

注：这里我还不会证明若后手不 \(skip\)，则先手一定会 \(skip\) 来获得子树内的最后一次操作的权利。~~感性理解下，感觉很有道理。~~
1. 偶树：我们声称若后手不 \(skip\)，则先手一定会 \(skip\) 来获得子树内的最后一次操作的权利。那么，先手有如下两种操作：
  1. 先手如果可以在偶树中 \(skip=0\) 获胜，则先手必胜。这是因为先手可以不停地在偶树中操作，那后手有两种可能：
    1. 操作了奇树，先手选择 \(skip\)；
    2. \(skip\) 了。
    上述两种情况都变成了情况 1.1，先手只需要模仿即可。
  2. 先手如果可以在奇树中 \(skip=1\) 获胜，则先手必胜。这是因为先手可以不停地在奇树中操作，那后手有两种可能：
    1. 操作了偶树，则先手选择 \(skip\)；
    2. \(skip\) 了。
    上述两种情况都变成了情况 1.1，先手只需要模仿即可。
    
    不过，先手也可以选择在操作奇树的时候 \(skip\)，所以是 \(skip=1\)。
    
    不过有个特例：假设偶树的大小为 \(0\)，则后手可以不选择操作偶树，所以，左子树就变成了 \(skip=2\) 的情况。
2. 奇树有两棵偶子树：我们枚举先手的第一次操作，于是对于后手就变成了 2.1 的局面。
3. 奇树有两棵奇子树：我们枚举先手的第一次操作，于是对于后手就变成了 2.1 的局面。
\(skip=2\)：

基本和 \(skip=1\) 类似。

偶树：根据状态定义，双方必定会有一方 \(skip\)，所以先手一定会获得子树内的最后一次操作的权利。那么，先手有如下两种操作：
1. 先手如果可以在偶树中 \(skip=0\) 获胜，则先手必胜。这是因为先手可以不停地在偶树中操作，那后手有两种可能：
  1. 操作了奇树，先手选择 \(skip\)；
  2. \(skip\) 了。
  上述两种情况都变成了情况 1.1，先手只需要模仿即可。
2. 先手如果可以在奇树中 \(skip=1\) 获胜，则先手必胜。这是因为先手可以不停地在奇树中操作，那后手有两种可能：
  1. 操作了偶树，则先手选择 \(skip\)；
  2. \(skip\) 了。
  上述两种情况都变成了情况 1.1，先手只需要模仿即可。
  
  不过，先手也可以选择在操作奇树的时候 \(skip\)，所以是 \(skip=1\)。
  
  这种情况不需要分偶树大小为 \(0\) 讨论，因为根据状态定义，若先手不 \(skip\)，后手必须 \(skip\)。
  
  所以只需要执行 \(skip=1\) 即可。
奇树有两棵偶子树：我们枚举先手的第一次操作，于是对于后手就变成了 3.1 的局面。
奇树有两棵奇子树：我们枚举先手的第一次操作，于是对于后手就变成了 3.1 的局面。

时间复杂度 \(O(n\log a)\)。

不过，我们可以把状态记成 \(\min/\max\) 从而避免二分。

时间复杂度 \(O(n)\)。

记录。

Ucup2 Stage5 Sets May Be Good

我们考虑计算 \(\sum_{S\subseteq\{1,2,3,\cdots,n\}} (-1)^{cnt(S)}\)，这里 \(cnt(S)\) 表示 \(S\) 集合的导出子图的边数。

我们记 \(x_i=[i\in S]\)。

我们考虑删掉 \(n\) 号点。

注意到如果 \(x_i\) 的取值会影响 \(cnt(s)\) 的奇偶性，则正负相消，贡献为 \(0\)。

所以我们需要保证下列条件满足：

\[\sum_{i=1}^{n-1}a_{n,i} x_i + a_{n,n}\equiv 0\pmod 2 \]

我们考虑是否存在位置 \(pos\)，满足 \(a_{n,pos}(pos\ne n) =1\)。

如果不存在这样的 \(pos\)，那我们根据 \(a_{n,n}\) 的取值分类讨论：
1. \(a_{n,n}=0\)，则贡献乘 \(2\)；
2. \(a_{n,n}=1\)，贡献变成 \(0\)。
如果存在一个位置 \(pos\)，满足 \(a_{n,pos}=1\)。

那么，根据 \(\sum_{i=1}^{n-1}a_{n,i} x_i + a_{n,n}\equiv 0\pmod 2\)，我们可以得出：

\[ x_{pos}\equiv \sum_{i=1\land i \ne pos}^{n-1} a_{n,i} x_i + a_{n,n} \pmod 2 \]

我们考虑对于一个序列 \(x_1,x_2,\cdots,x_n\) 计算答案。

\[\begin{aligned} &\sum_{i=1}^{n}\sum_{j=i+1}^n a_{i,j} x_i x_j\\ \equiv&\sum_{i=1}^{n-1}\sum_{j=i+1}^{n-1} a_{i,j} x_i x_j\\ \equiv&\sum_{i=1\land i \ne pos}^{n - 1}\sum_{j=i+1\land j\ne pos}^{n - 1} a_{i,j} x_ix_j+\sum_{i=1\land i \ne pos}^{n-1} a_{i,pos} x_ix_{pos} + a_{pos,pos}x_{pos}\\ \equiv&\sum_{i=1\land i \ne pos}^{n - 1}\sum_{j=i+1\land j\ne pos}^{n - 1} a_{i,j} x_i x_j+\sum_{i=1\land i \ne pos}^{n-1} a_{i,pos} x_i(\sum_{i=1\land i \ne pos}^{n-1} a_{n,i} x_i+a_{n,n})+a_{pos,pos}(\sum_{i=1\land i \ne pos}^{n-1} a_{n,i} x_i+a_{n,n}) \end{aligned} \]

于是，我们就可以把 \(n\times n\) 的矩阵，在 \(O(\frac{n^2}{w})\) 的时间内，变成 \((n-2)\times (n-2)\) 的矩阵。

注意到 \(x_n\) 有两种取值，所以贡献要 \(\times 2\)。注意到上述式子继续展开，则 \(a_{pos,pos}a_{n,n}\) 的项，所以贡献可能 \(\times (-1)\)。

总时间复杂度 \(O(\frac{n^3}{w})\)。

记录。

Ucup2 Stage6 A Digital Nim

考虑裸暴力：

F(i,1,n){
	F(j,1,D(i))if(!f[i-j]){
		f[i] = 1;
		break;
	}
}

那显然，我只关心 \(f_{pos}=0\) 最后的 \(pos\)，记录和当前 \(i\) 的差 \(las\)，如果 \(dightsum \ge las\)，则 \(f_i=1\)，否则 \(f_i=0\)。

于是不可以不断更新 \(las\)。

注意到 \(dightsum \le 17\times 9\)，所以 \(las\) 的一个很松的上界是 \(17\times 9\)。因为不可能出来连续 \(17\times 9\) 个 \(1\)。

考虑 DP of DP。我们在高位进行增加，那么我就不影响之前的位。我们记 \(f_{bit,las,presum,delta}\) 表示当前让第 \(bit\) 位增加 \(1\)，增加前 \(las\) 的值，第 \(i\) 位前面位的和的值，这一位增加 \(delta\)，并记录增加之后 \(las'\) 的值。

预处理之后，每次只要把询问的数在 \(10\) 进制下分解一下，求出最终 \(las\) 的值。

时间复杂度 \(O(\log_{10} ^3 x \times 10^3 + q\log x)\)。

CF1884E Hard Design

我们先考虑如何对原序列计算答案的一种做法。

我们考虑按最大值建笛卡尔树。假设我们所在笛卡尔树节点为 \(x\)，在笛卡尔树上的父亲为 \(fa_x\) 我们考虑在这个笛卡尔树区间操作 \(a_{fa_x}-a_x\) 次。

考虑如何处理 \((r-l+1)^2\)。我们考虑组合意义，相当于是任意选两个位置的方案数。那么，我们现在考虑两个位置 \(x,y\) 能被同时选到的方案数如何计算。我们找到 \(x,y\) 的祖先 \(k\)，也就是说，在 \(k\) 即 \(k\) 的祖先之前，\(x,y\) 都会被同时选到，贡献即为 \(a_{fa_{k}}-a_k+a_{fa_{fa_k}}-a_{fa_{k}}+\cdots+a_{rt}=a_{rt}-a_k\)。所以说，我只需要在 \(LCA\) 出计算两部分的贡献即可。

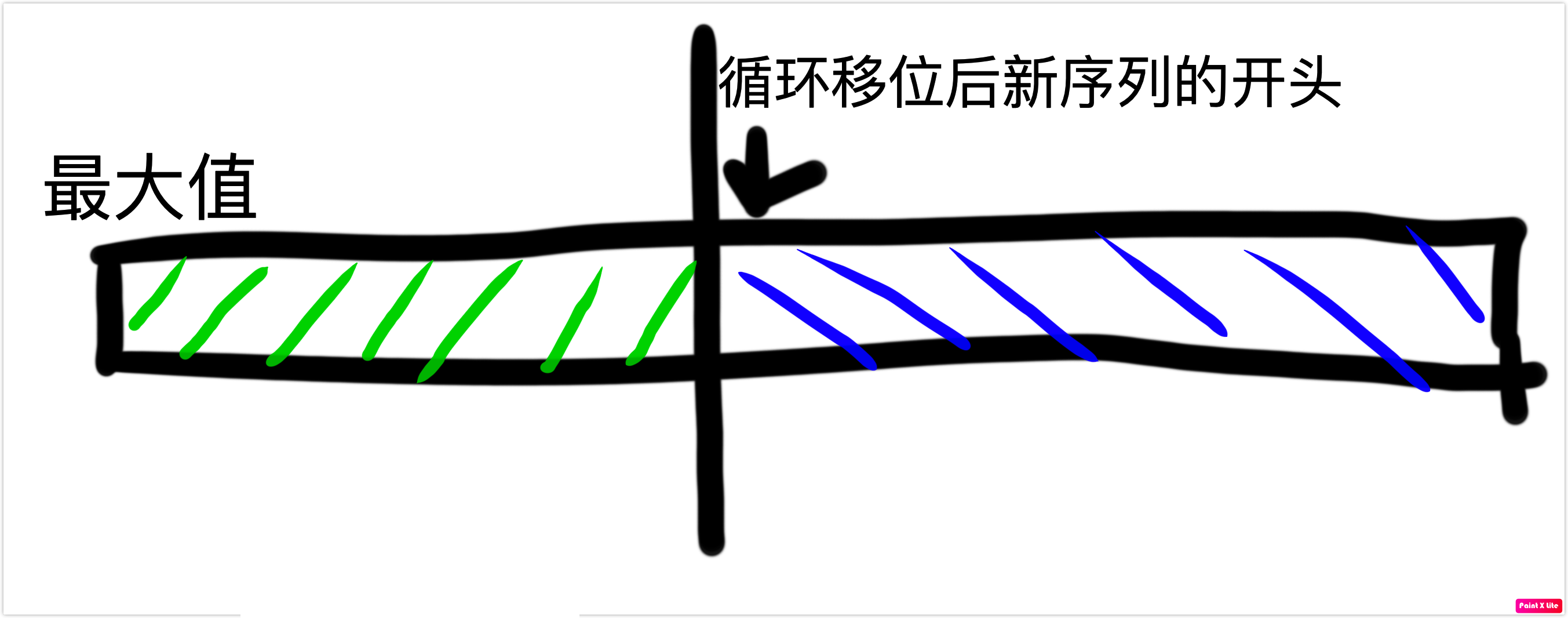
我们再考虑原问题。首先，最大值的左右两部分是独立的，因为最大值肯定不会被操作。那么，原序列就被划分成了两个部分，而这两个部分恰好对应了以最大值作为开头的一段前缀和一段后缀。

那我们就先可以出计算 \(vl_i\) 表示 \(i\) 作为一对数的右端点的贡献，\(vr_i\) 表示 \(i\) 作为一对数的左端点的贡献。

计算时考虑建出笛卡尔树，然后计算左子树对右子树的贡献（\(vl\)）以及右子树对左子树的贡献（\(vr\)）。当然笛卡尔树并不需要显示地建出来，可以直接单调栈求出每个数作为最大值的区间即可。

然后再对 \(vl_i,vr_i\) 分别做前缀和、后缀和，即可得到前缀、后缀的贡献和。

时间复杂度 \(O(n)\)。

记录。

posted @ 2023-10-07 11:24 zhaohaikun 阅读(196) 评论(2) 编辑收藏举报

刷新页面返回顶部

zhaohaikun

希望如火，失望如烟！