2023 年 9 月训练记录
训练记录
9 月没做题。
不能摆了，再摆就完蛋了。
CF1784F Minimums or Medians
很厉害的题。
我们考虑找充要条件：
-
注意到所有被删除的连续段长度都是偶数。并且不同的连续段之间，都是被分开删除的。
注意到只有从 \(1\) 开始的连续段才可能用操作 1 删除，于是其它被删的数都是通过操作 2 删除的。
-
注意到第 \(i\) 次若为操作 2，则删除的较大数为 \(i+n\)，所以，被删除的数都必须 \(\le n+k\)。
-
注意到若删除了数 \(t\le n\) 不在第一段，则 \([t,2n-t+1]\) 的数都必须被删除。
上述 3 个必要条件是充分的，因为考虑我可以通过构造，每次能用操作 2 就用操作 2，否则就用操作 1，不难发现一定是合法的。
设函数 \(f(n, m)\) 表示长度为 \(n\) 的段中，选出 \(2m\) 个数，并要求选出的数形成长度为偶数的连续段。考虑捆绑法，我们没选出一个数就要求必须选它后面的那个数，于是这样就只有 \(n-m\) 个物品，从中选出 \(m\) 个，所以是 \(\binom{n-m}{m}\)。
考虑如何计数。首先，我们枚举从 1 开始的连续段需要操作的次数 \(t\)，因为涉及到条件 3，所以我们需要根据是否覆盖超过一半来分类讨论：
- \(2t < n\)，于是再枚举在 \(n\) 之前被删掉的连续段长度 \(c\)，于是得到：
注意到 \(len\) 增加时，组合数的变化可以 \(O(1)\) 维护，类似莫队移动指针，加入或删除组合数。
- \(2t \ge n\)，那么剩下的就可以随便操作，于是对答案的贡献为：
记录。
CF325E The Red Button
爵士好题。
首先，主要到每个点出度为 \(2\)，并且入度为 \(2\)。
注意到 \(n\) 为奇数无解。因为 \(0\) 和 \(n-1\) 都有自环，并且另一条入边都是从 \(\frac{n-1}{2}\) 连出的。
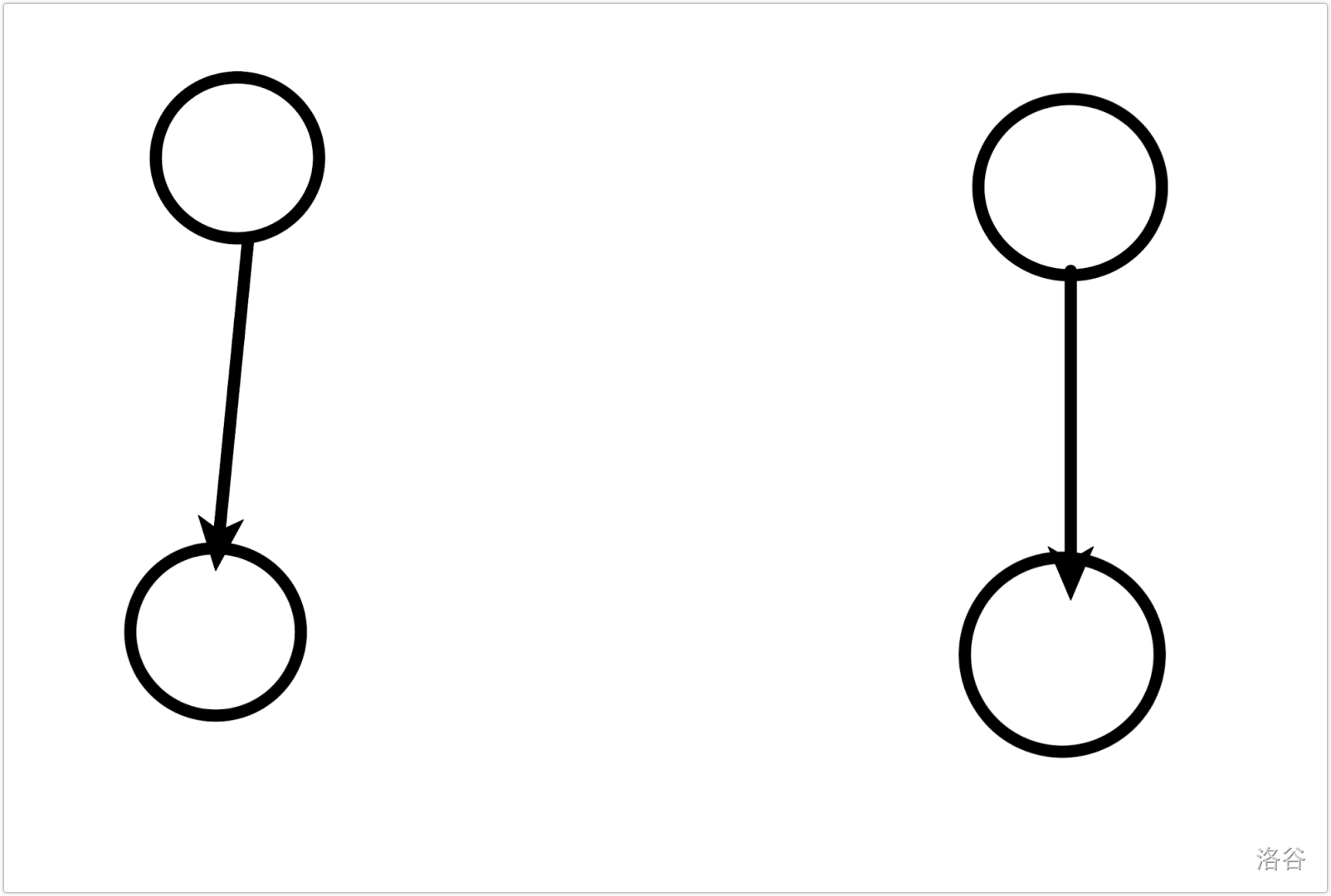
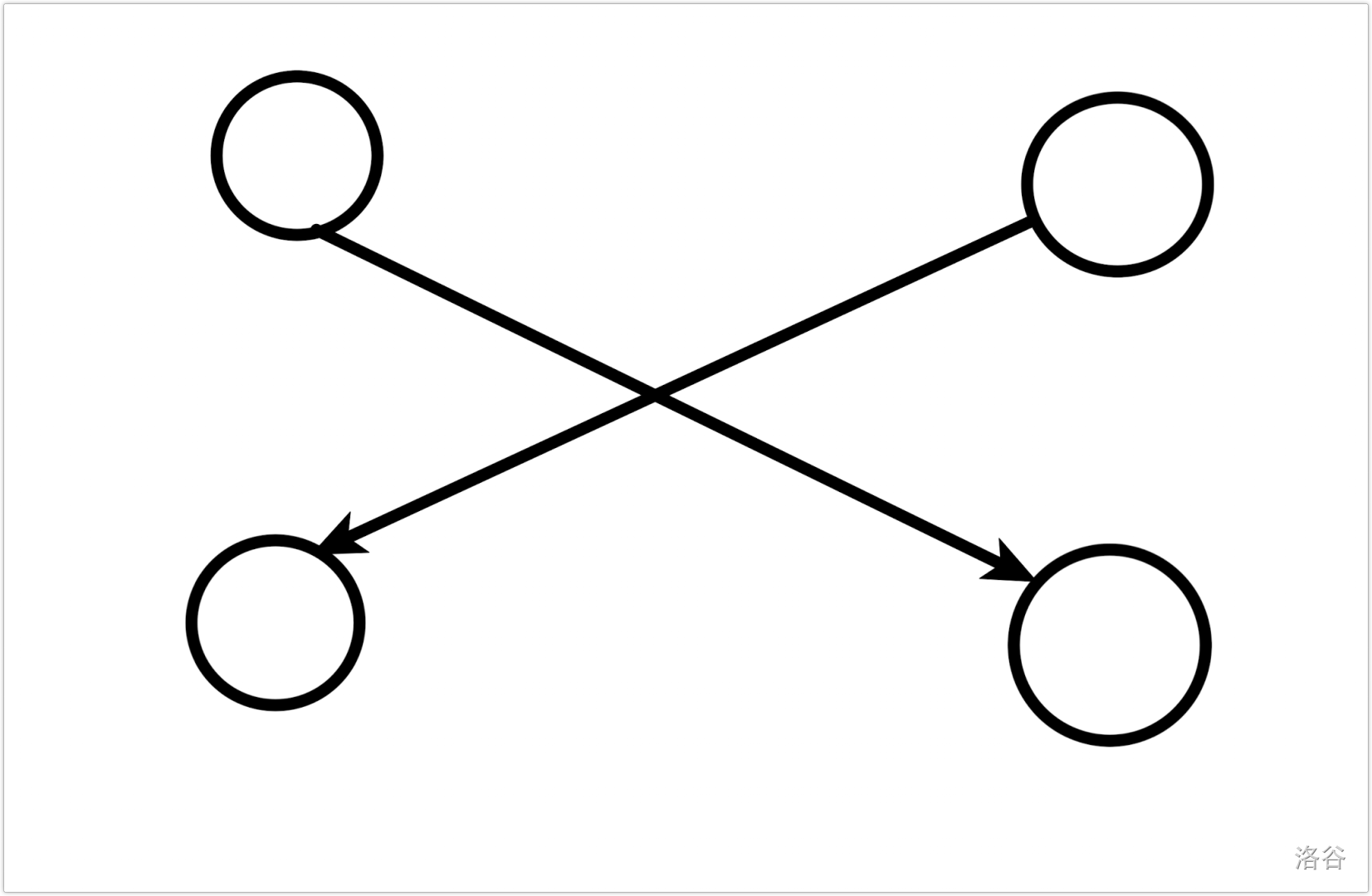
考虑 \(n\) 为偶数。由于入度、出度都为 \(2\)，所以相当于在求欧拉回路。注意到 \(i(i<\frac{n}{2})\) 和 \(i+ \frac{n}{2}\) 的出边是一样的。我们先让他们任意选。
这样可能会出现小环，于是我们直接交换下他们所选的边就可以了。
变成
记录。
CF896D Nephren Runs a Cinema
首先，原问题相当于是从 \((0,0)\) 出发，每次让 \(y\) 增加 \(1\)、不变、减少 \(1\)，要求过程中不能出现 \(y<0\)。
肯定是考虑经典的反射容斥：
我们考虑枚举 y 不变的次数和最终的 y。
定义 \(path(x, y)\) 表示从 \((0,0)\)，每次让 \(y\) 增加 \(1\)、减少 \(1\)，最终走到 \((x,y)\) 的方案数，为 \(C(x, \frac{x+y}{2})\)。
所以，从 \((0,0)\) 走到 \((x,y)\)，并且不经过 \(y=-1\) 的方案数为：\(path(x, y)-path(x,-2-y)\)，相当于按 \(y=-1\) 翻折。
注意到前后会互相抵消，所以得到：
这里 \(tl\) 和 \(tr\) 表示跟 \(\equiv n-i \pmod 2\) 最小、最大的在 \([l,r]\) 范围内的 \(j\)，显然可以 \(O(1)\) 求出。
不过这题有个比较恶心的地方在于模数不保证质数，所以，我们考虑先将质数分解质因数，变成 \(\prod_i p_i^{a_i}\)。
我们维护答案 \(p_i\) 的次数，这样答案被我们处理成了两部分，一部分是 \(p_i\) 这样的质因子，另一部分 \(\perp mod\)。
我们考虑除法，对于 \(p_i\) 这样的质因子，我们直接次数相减；对于 \(\perp mod\) 的部分，我们用 \(exgcd\) 求出在 \(\pmod {mod}\) 意义下的逆元。
最后考虑还原答案，注意到答案一定是正整数，也就是说最终一定是整数，所以次数一定非负。
如果答案不为整数，并且存在 \(p_i\) 次数小于 \(0\)，那说明答案在 \(\pmod {mod}\) 意义下不存在。
关于算组合数有两种处理方法：
- 直接用上面的方法预处理出 \(fac,ifac\)；
- 注意到我们可以把式子中的 \(\binom{n-i}{\frac{n-i+tl}{2}}\) 和 \(\binom{n-i}{\frac{n-i+tr}{2} + 1}\) 分开，两部分组合数上下变量的变化次数都是 \(O(n)\) 的。而组合数上下变量加减 1 都是好做的。
时间复杂度 \(O(n\log p)\)。
记录。
CF750G New Year and Binary Tree Paths
我们考虑枚举 LCA 左右两侧的链长，令 LCA 为 \(x\)，左链长为 \(a\)，右链长为 \(b\)，记左链路径上的 01 状态为 \(u\)，右链 01 状态为 \(v\)，则和为 \((2^{a+1}+2^{b+1}-3)x + f(u)+f(v)\)。
其中，\(f(x)\) 表示链上 01 状态的贡献。因为每个 \(2^i\) 都有 \(2^{i+1}-1\) 的贡献，所以 \(f(x)=2x-popcount(x)\)。
于是，我们再去枚举左右链的 \(popcount\) 和，然后就可以 DP 了。我们令 \(f_{i,j,0/1}\) 表示从低往高第 \(i\) 个二进制位，\(popcount\) 和为 \(j\)，进位为 \(0/1\) 的方案数。
最后要求 \(popcount=\) 枚举的 \(popcount\)。
祖先后代链的情况要特判一下，这是容易的。
时间复杂度 \(O(\log^5 s)\)。似乎可以进一步分析得到 \(O(\log^4 s)\) 的做法，但我不会 /ll。
记录。
CF811E Vladik and Entertaining Flags
解法 1
由于 \(n\) 很小，我们考虑对 \(m\) 列，线段树维护当前区间的连通性，也就是最左、最右的并查集状态，以及内部连通块个数。考虑 pushup 的时候，相当于增加一些边，那就在并查集上合并一下，这是好维护的。
时间复杂度 \(O((m+q)n\log m)\)。
解法 2
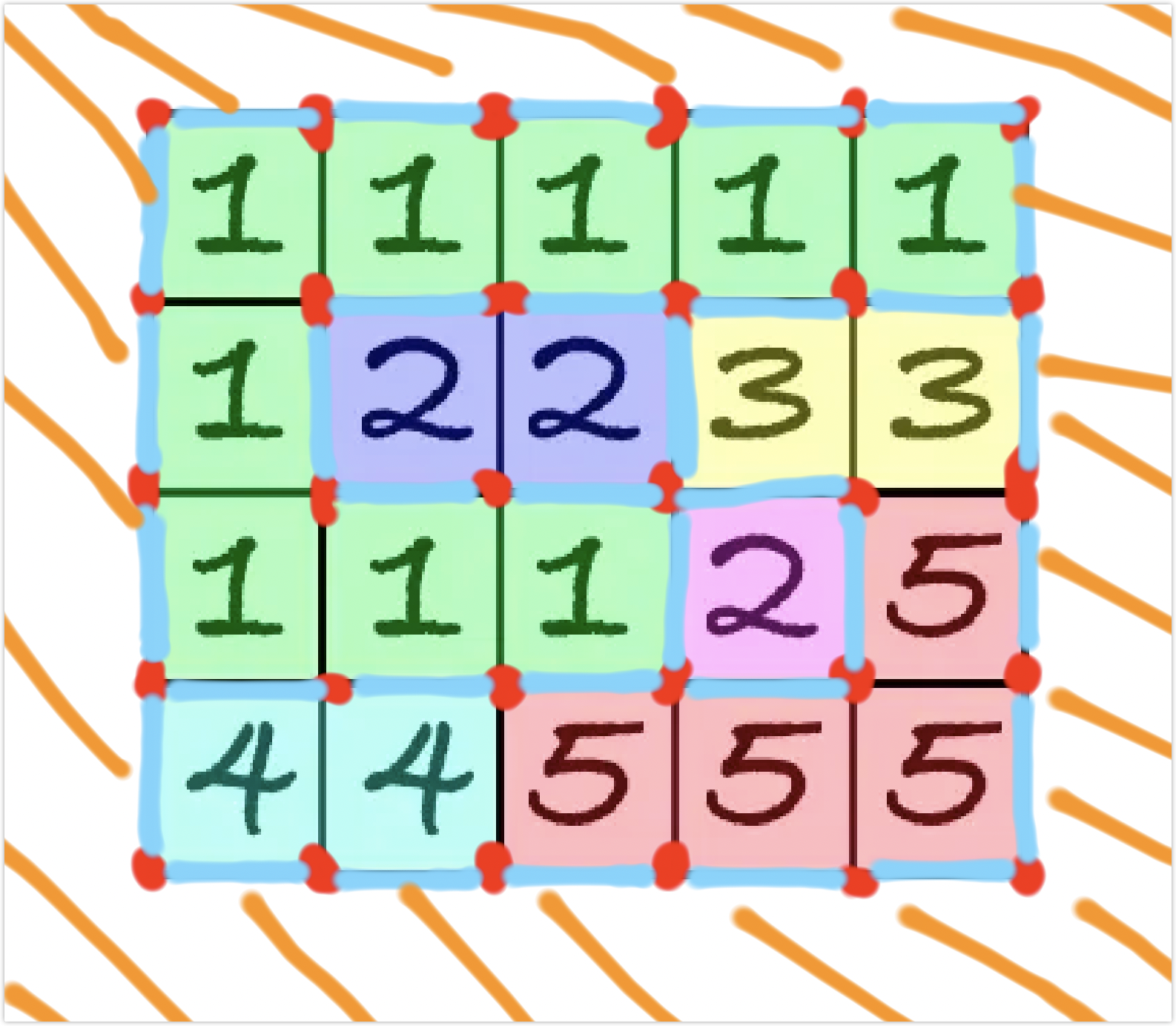
考虑欧拉定理。对于一个平面图，一个连通块划分的面数 \(R\)，满足 \(|V|-|E|+|R|=2\)。证明考虑归纳，加上一条边时要么增加一个面，要么增加一个点。
但是题目给定的不一定是连通块。我们分析一下，发现按照这个公式算出的结果，每多一个连通块，那 \(|R|\) 就会被我少算 \(1\)。考虑平面上增加一个点，那 \(R\) 是不变的，但点数增加了 \(1\)，所以导致我们的 \(|R|\) 被少算了 \(1\)。
注意，橙色部分也是会被统计成连通块的。
\(|V|\) 和 \(|E|\)，是好算的，现在我们要算被严格包含的连通块数量。
这也是好做的，我们考虑把图建出来，然后每个连通块有个最左、最右的界。于是，现在就变成了一个二维数点问题了。
时间复杂度 \(O(nm\log m + q\log m)\)。
记录。
CF981H K Paths
我们考虑枚举路径 LCA 为 \(x\)，那么相当于对于 \(x\) 的子树，我们都求出 \(f_x\) 表示路径的一个端点为 \(x\)，则 \(x\) 往下延伸有多少种方案数。
这个相当于是 \(\sum_{t=0}^{k}[x^t]\prod_{i\in son_x} (sz_i x + 1)\)，这是好算的，我们直接分治 NTT 即可。
我们设 \(g_x\) 为 \(f_x\) 的子树和，这样相当于表示端点在 \(x\) 子树内，并且向下延伸的方案数。
然后，我们考虑计算非祖先后代情况的答案，相当于是 \(\sum_{i,j\in son_x} g_i g_j\)。
祖先后代情况更困难，相当于是 \(\sum_{i\in son_x} g_i \prod_{t=0}^{k} [x^t]((n - sz_x) x + 1) \prod_{j\in son_x \land i\ne j} (sz_jx+1)\)。
不过，这个依旧是可以分治 NTT 的。
注意到上面的式子，相当于是只有一项选择了 \(g_i\)，其它全选择了 \(sz_jx+1\)。
我们考虑维护 \(t_{0/1}\) 表示当前区间，是否选择了 \(g_i\)。合并两个区间时，对于 \(t_{1}\)，那肯定是其中一个区间的 \(t_1\) 乘另一个区间的 \(t_0\)；对于 \(t_0\)，肯定是两个区间的 \(t_0\) 乘起来。
时间复杂度 \(O(n\log ^ 2n)\)。
记录。
「2019 集训队互测 Day 3」操作序列计数
给雷暴磕头了。
曾经的 LOJ 最优解，不过当我写做题记录时已经不是了/ll。
注意到最后答案相当于选了 \(\sum_{i=0}^{lim} cnt_ik^i + adjust=n\)，相当于有一个 \(adjust\) 的变量，把 \(\le n\) 转化成了 \(=n\) ，这里 \(lim\) 表示 \(2\) 操作的次数，显然 \(lim\) 是 \(\log n\) 级别的，于是我们考虑直接枚举（实际上题目也要求我们枚举）。
思考下 \(lim\) 的限制，我们要求 \(cnt_{lim} >0\)，因为初始有个 \(1\)，不过这个限制我们可以容斥掉。我们令 \(f_i\) 表示 \(lim=i\) 忽略 \(cnt_{lim}>0\) 的答案，那么 \(lim=i\) 的正确答案，其实就是 \(f_{i}-f_{i-1}\)。
于是现在我们就只需要考虑计算 \(f_i\)。我们观察到 \(k^i\) 这个形式，所以一个很妙的想法是，我们把 \(cnt_i\) 也变成 \(k\) 进制。
我们考虑 DP，令 \(f_{i,j}\) 表示在第 \(i\) 位前，总共有 \(j\) 的进位的方案数，中间需要预处理 \(g_{i,j}\) 表示 \(i\) 个数和为 \(j\)，每个数 \(<k\) 的方案数。
对于 \(i>lim\) 的部分，我们枚举到第 \(i+1\) 的进位 \(j\)，那么剩下的部分和是确定的，令其为 \(t\)。之后的过程相当于是把 \(t-j\) 拆分成 \(i\) 个非负整数的方案数，显然是 \(\binom{t-j+i + 1}{i + 1}\)。
时间复杂度（不考虑高精度） \(O(\log^3 n+k^2\log^2 n)\)。
记录。
CF1864H Asterism Stream
给验题人雷暴磕头了。
基本跟上一题一个做法，这里写的简略一点了。
首先，我们转化成计算所有数出现的概率和。
我们同样考虑枚举操作二的次数 \(lim\)，上界是 \(\log n\) 的，系数为 \(\frac{1}{2^L}\)。然后，我们转化成 \(\sum_{i=0}^{lim} cnt_i 2^i + adjust=n\)。
那么对应的系数就是 \(2^{\sum_{i=0}^{lim}cnt_i}\)，然后就完全一样了，直接把上面预处理的 \(g_{i,j}\) 换一下就可以了。
由于这题跟操作次数关系密切，所以 \(i>lim\) 的部分不能用组合数的方法快速求出。
时间复杂度 \(O(t\log^4 n)\)。
记录。
CF1149D Abandoning Roads
雷暴推荐的题，大家都喜欢.jpg。
首先，我们先把边权为 \(a\) 的边给缩起来，因为在最小生成树中，这些连通块内部肯定是边权为 \(a\) 的边。然后，我们考虑一条可能在最短路上的路径需要满足什么条件，分析一下其实就是不能到某个连通块超过两次。
于是现在就有了一个 \(O(m 2^n\log (m2^n))=O(nm2^n\log m)\) 的做法，就是令 \(f_{i,mask}\) 表示当前到 \(i\) 号点，到过的连通块状态为 \(mask\)。
不过注意到 \(a<b\)，所以连通块大小 \(\le 3\)，出现不合法情况不会使答案更优。
所以，我们只需要记录大小 \(\ge 4\) 的连通块的状态，于是时间复杂度 \(O(m 2^{\frac{n}{4}}\log (m2^{\frac{n}{4}}))=O(nm2^n\log m)\)。
更进一步：实际上复杂度里的 \(\log (m2^{\frac{n}{4}})\) 是可以去掉的。
考虑一个问题：对于一个 \(n\) 个点，\(m\) 条边的图，我需要求 \(1\) 到 \(n\) 的最短路，并且边权只有 \(k\) 种取值。这个问题可以 \(O(mk)\) 的。
做法是这样的。我们维护 \(k\) 个队列，表示最短路上一次是有第 \(i\) 种边权更新的，那我每次新加入的，按最短路排序肯定是直接放在末尾的。每次找没有去松弛过别的点的最短路最小的点时，我们直接对这 \(k\) 个队列对它们的队头求最小值的位置即可。
这个东西算是 01 BFS 的一个拓展。
回到本题，\(k=2\)，所以我们的复杂度是 \(O(m2^{\frac{n}{4}})\) 的，优势在我。
CF1817D Toy Machine
VP 写了个随机化没过 /ll。
烂烂 烂烂 烂烂 烂烂 烂烂 烂烂 烂烂 烂烂 烂烂 烂烂。
烂烂 Ad-hoc。
——Alex_wei
对于 \(k\le \frac{n-1}{2}\) 的情况，我们执行 \(k-1\) 次 LDRU，然后再执行一次 L，这样就可以移到最前面了。这还是可以想到的。
对于 \(k>\frac{n-1}/2\) 的情况，我们可以对称地先把 \(k\) 移到最右边。然后不断执行 RDRU 直到所有数全部堆在右半部分，且 \(k\) 在右上角，再执行一次 LU，\(k\) 就变到了原来 \(\frac{n-1}{2}\) 的位置，再用上面的方法做一遍就可以了。
时间复杂度 \(O(n)\)。
记录。
JOISC2017G 長距離バス (Long Distance Coach)
模拟赛 \(O(n\log ^2 n)\) 通过了这道题，很有感觉。
我们考虑按照模 \(T\) 的余数分段，于是每个饮水机相当于是能让一段区间的后缀全部不合法。于是我们考虑 DP，令 \(f_i\) 表示只考虑前 \(i\) 个人的最小代价。
我们分两种情况讨论。第一种是这个人没有被违约，从 \(f_{i-1}\) 转移过来，\(f_{i-1}+c_iw\to f_i\)，这里 \(c_i\) 是需要喝水的次数。第二种情况是这个人是最后一个被违约的，我们先枚举区间，然后再找可行的转移，\(f_{j-1}+val_k(i - j + 1) + sum_i-sum_{j-1},j\in[l_k,r_k]\)。
不难发现是关于 \(j\) 的一次函数形式。由于都是后缀查询，所以我们考虑树状数组套李超树来解决这个问题，时间复杂度 \(O(n\log ^ 2n)\)，这是我的赛时做法。
实际上，我们观察下性质。注意到，对于区间 \([l_k,r_k]\)，由于起点饮水机的存在，所以对于任意一个饮水机，它前面肯定还有其它饮水机，所以对于 \(l_k\) 前面的位置，肯定是不会比 \(val_k\) 劣。
所以，我们不需要树状数组，直接全局查询即可。
时间复杂度 \(O(n\log n)\)。
记录。
[Code+#7] 六元环
给雷暴磕头。
首先，有个结论是，六元环个数等于笛卡尔树上不包含根的大小为 \(4\) 的连通块个数。
然后我们考虑修改如何处理。由于都是加正数，所以我们每次相当于把一个点往上旋。那么，我们考虑把同侧儿子的链给并起来，每次一起做。
可以证明，这样操作次数均摊 \(O(1)\)。
之后，我们考虑如何找同侧链的链顶。我们额外唯一一个线段树，维护整个序列。查询链顶以左儿子为例，就相当于找到右侧第一个大于它的数。如果修改后比这个数还大，那我就直接把当前数选到链顶。否则，我需要在链上找到它最大能选到的位置。同样以左儿子为例，这实际上只需要在线段树左侧第一个比它修改后大的位置的右儿子。右儿子都是同理。
考虑 zig-zag 如何实现。注意到大小为 \(4\) 的连通块个数，对于要选的点 \(x\)，只会影响它往上的 \(4\) 个祖先，选到之后也只会影响 \(4\) 个祖先，pushup 也是 \(O(1)\) 的，只需要做 \(4\times 4\) 的卷积。
时间复杂度 \(O(q\log n)\)。
记录。
CF1148G Gold Experience
我们考虑对 \(\gcd=1\) 的数对建边。这样题目的条件就变成了：
- 选的点构成独立集；或
- 选的点都构成大小 \(\ge 2\) 的连通块。
我们考虑这样一种构造方法：
首先，我们按照编号顺序，从小到大对每个数判断是否可以加入独立集，能加就加。这样就可以得到一个极大的独立集。
关于如果判断是否有数互质，可以使用莫比乌斯反演，得到 \(\sum_{t\in S} [a_x|t]=\sum_{t\in S} \sum_{i|t\land i|a_x} \mu(i)= \sum_{i|a_x} \mu(i)cnt_i\)，这里 \(S\) 是当前极大独立集，\(cnt_i\) 表示 \(S\) 中是 \(i\) 倍数的个数。
如果说这个独立集大小 \(\ge k\)，那么就结束了。否则，由于独立集是极大的，我们可以对每个数找到一个和它互质的数，作为它的集合中的数，这个过程可以整体二分来实现。
由于题目中给出的 \(2k\le n\) 的条件，那么我们就可以选择若干独立集的点作为代表元，再选它们子集中的一些数，从而形成大小 \(\ge 2\) 的连通块。
时间复杂度 \(O(n \log n 2^w)\)，瓶颈在整体二分。
记录。
[CERC2013] History course
注意到“两个区间如果没有交点，则左端点更小的区间需要排在前面“，这个限制其实是没有用的。因为如果不满足这个条件，调整成这样一定是不劣的。
最小化最大值的一个很套路的想法是二分答案。
考虑如何判断。我们先把序列按左端点排序。我们逐个位置地确定选择的区间。一个贪心的策略是，每次选择能选出并且不会立即造成不合法的，右端点最左的。
这样是正确的，因为既不会立即造成不合法，并且对后面位置的影响最小。
考虑如何维护这个过程。我们先对未选出的区间维护 \(lim_i\)，表示 \(i\) 区间最后能放在距离当前位置的多少个位置之后。由于我们按照了左端点排序，所以我们维护的指针 \(pos\) 表示当前最前没有被限制到的区间的位置，每次不断更新。
我们考虑什么时候会出现不合法。相当于每个左部点能匹配右部点的一个前缀，所以根据 Hall 定理，当且仅当在 \(lim_i>cnt_i\) 的时候不合法，\(cnt_i\) 表示在 \(i\) 之前（包含 \(i\)）没有被选择的区间数量。注意到每选一个区间后，\(lim_i\) 都会集体减少 \(1\)，而 \(cnt_i\) 是一个区间减一，都是好维护的。
令 \(t_i=lim_i-cnt_i\)，每次选区间时，如果出现 \(t_i<0\)，那已经不合法。如果有 \(t_i=0\)，那我们找到第一个，令其为 \(pos\)。这就要求我们选择的区间编号要在 \([i,pos]\) 当中，否则 \(t_pos<0\)。于是，我们就在这个区间中，找右端点最小的区间即可。
构造方案就按上面的即可。
时间复杂度 \(O(n\log ^ 2 n)\)。
记录。
CF101E Candies and Stones
记录下输出方案 DP 卡空间的多种做法。
做法 1
我们发现直接用 bitset 优化空间就比题目要求的空间限制大了一点，所以我们就将 DP 拆成两半即可。
空间复杂度 \(O(\frac{nm}{w})\)。
做法 2
我们考虑根号平衡。我们先完整地做一遍 DP，每 \(B\) 个记录一整行的 DP 值。
然后输出方案考虑从后往前对每个块再做一遍 DP，倒推出方案，记录下到这个块开头的决策位置。
直接做空间复杂度是有两部分：
- 记录 DP 值：\(O(\frac{nm}{B})\)。
- 第二遍 DP 记录方案：\(O(Bm)\)。
认为 \(n,m\) 同阶，所以 \(B=\sqrt{n}\) 最优。
注意到第二部分可以用 bitset，于是空间复杂度就变成了 \(O(\frac{nm}{B}+\frac{Bm}{w})\)。
取 \(B=\sqrt{nw}\)，得到空间复杂度为 \(O(n\sqrt{\frac{n}{w}})\)。
做法 3
考虑分治，假设当前分支的区间为 \(i\in[l_1,r1],j\in[l_2,r_2]\)，表示当前知道 \(f_{l_1,r_1}\)，要求 \(f_{l_2,r_2}\)，并构造方案。我们先做一遍 DP，记录下 \(f_{\lfloor\frac{l_1+r_1}{2}\rfloor},j\) 的值，从而得到在第 \(\lfloor\frac{l_1+r_1}{2}\rfloor\) 行的决策点位置 \(pos\)。于是分治区间就拆成了 \([l1,\lfloor\frac{l_1+r_1}{2}\rfloor],[l_2,pos]\) 和 \([\lfloor\frac{l_1+r_1}{2}\rfloor + 1,r_1],[pos,r_2]\)。
注意到如果我们把分治区间看成一个矩形，那时间复杂度就是矩形的面积。而我们一次分治会让矩形的面积除 \(2\)。
所以时间复杂度和空间复杂度是 \(O(nm+\frac{nm}{2}+\frac{nm}{4}+\cdots) = O(\sum_{i=0} \frac{nm}{2^i})=O(nm)\)。
CF436E Cardboard Box
我们考虑一种反悔贪心的策略：假设当前已经选择了若干数，我们想新选一些数。如果当前还需要选一个数，那我们肯定会选择没选过中的 \(a_i\) 最小的、以及取过中的 \(b_i-a_i\) 最小的，这两种决策取最优。
但如果说我们还需要选不止一个数，我们还有一种决策是一次选两个数，选择没选过的 \(b_i\) 最小的。然后，我们比较连续两次选一个数和选两个数哪种更优。
时间复杂度 \(O(n\log n)\)。
记录。
ARC080F Prime Flip
做过一个非常类似的题，所以模拟赛场切了。
考虑奇质数的性质，我们想到哥德巴赫猜想。由于 \(\ge 6\) 的偶数都可以被表示成两个奇质数的和，而 \(2=5-3,4=11-7\)，所以任何偶数都可以用两个奇质数组合。
我们考虑把区间翻转转换成修改差分。也就是我们需要把差分为 \(1\) 的位置全部变成 \(0\)。
我们考虑将这些 \(1\)，两两匹配，于是我们讨论一下代价：
- 下标差为奇质数：代价为 \(1\)；
- 下标差为偶数：代价为 \(2\)；
- 下标差为奇非质数：代价为 \(3\)。
我们考虑一种贪心策略。我们先尽可能匹配奇质数，对于剩下的再将奇偶性相同的用偶数匹配，其它再用奇非质数来处理。
考虑这样做为什么是对的。因为如果我们将奇质数和奇非质数的操作，变成两次下标差为偶数的，代价从 1+3 变成了 2+2，所以优先匹配奇质数是不劣的。
由于差是奇质数，所以一定是一奇一偶匹配，所以图是二分图，可以跑 \(dinic\)。
时间复杂度 \(O(n^3)\)。
CF1452G Game On Tree
对于 Alice 而言，一个可行的终点当且仅当 Alice 卡片到这个位置的距离 \(\le\) Bob 任何一张卡片到这个位置的距离。
我们考虑对每个点求出 \(f(x)\) 表示的 Bob 卡片到点 \(x\) 最近的距离是多少。这个可以通过将 Bob 的所有卡片为起点求最短路得到。
然后，我们相当于可以对距离 \(x\) 不超过 \(f(x)\) 的点作为起点的答案，更新 \(x\) 作为终点的答案。
我们考虑用点分治来实现这个过程。注意到点分治的查询操作可以用预处理前缀 \(\max\) 来完成。并且由于 LCA 不为当前分治中心肯定不会更优，所以我们不需要要求两点不来自同一个子树。
时间复杂度 \(O(n\log n)\)。
记录。
ARC165E Random Isolation
好题，VP 时没做出来。
首先，我们可以转化成选择一个排列，如果可以操作就有 \(1\) 的贡献。
由于期望的线性性，我们考虑对每个点每种被选时包含它的连通块的状态算贡献。
假设我们确定了选 \(x\) 时，连通块内有哪些点。我们令 \(S\) 表示与 \(x\) 连通块直接有边且不在这个连通块内的点。
那对应的概率就是要求 \(S\) 中的点要排在 \(x\) 前面，而 \(x\) 连通块内的除了 \(x\) 的其它点排在 \(x\) 后面。注意到我们已经钦定了 \(x\) 所在连通块大小超过 \(K\)，所以与 \(S\) 中的点排在 \(x\) 前面就一定会被操作。
于是，我们记 \(f_{x,i,j}\) 表示 \(x\) 子树内选了 \(i\) 个点，\(|S|=j\)。每次枚举根的时间复杂度为 \(O(n^5)\)，常数非常小，可以通过。
不过，我们也可以通过只做一次树形 DP。我们对连通块计数，并在连通块内深度最浅的那个点统计答案即可。
时间复杂度 \(O(n^4)\)。
记录。
ARC150D Removing Gacha
同样考虑先转化成选排列按顺序操作，然后我们对每个点统计贡献。
我们令 \(d_i\) 表示根节点到 \(i\) 经过的节点数。那么 \(i\) 产生贡献就要求 \(i\) 在这 \(d_i\) 个点中最后一个被选。
所以答案是 \(\sum_{i=1}^{n} \frac{1}{d_i}\)。
时间复杂度 \(O(n)\)。
记录。
ARC108E Random IS
这个题虽然也可以转化成选择排列，但转化之后并不好计数，因为我不能很好地判断一个点是否可以被选上。
我们考虑判断一个位置是否能被选到上升子序列中，只跟它前后的两个位置有关。也就是说，我选择一个位置之后，它左右两边就独立了。
于是，我们可以令 \(f_{i,j}\) 表示左边上一次被选的位置为 \(i\)，右边上一次被选的位置为 \(j\)，期望选的次数。
为了方便，我们令 \(a_{0}=-\infty,a_n=\infty\)，这样答案就是 \(f_{0,n}\)。
朴素地转移可以做到 \(O(n^3)\)，不过可以用树状数组优化，时间复杂度 \(O(n^2\log n)\)。
记录。
ARC165F Make Adjacent
注意到由于要最小化 \(k\)，所以我们可以来简单讨论一下。
假设有 A、B 两个数，不妨假设第一个位置是 A。
- A A B B：必须是 A A B B；
- A B A B：必须是 A A B B；
- A B B A：可以是 A A B B，也可以是 B B A A。
也就是说所以 A A B B、A B A B 这样的数对，A 都必须排在前面。
做法 1
JCY 的做法：于是有一种不要脑子的做法是，我们可以主席树优化建图，然后求出字典序最小的拓扑序。
时间复杂度 \(O(n\log n)\)。
做法 2
我的做法：由于是字典序最小，所以我们可以考虑第一个位置有哪些数可以选。我们发现它们形成了一个不断包含的结构。于是我们把它们求出来，然后使用堆来维护值最小的位置。
维护当前可以放在第一个位置可以用线段树二分维护。
需要讨论一下，都是可以维护的。
时间复杂度 \(O(n\log n)\)。
记录。
做法 3
雷暴的做法：注意到我做法中那个不断包含的结构，实际上就是要求右端点是前缀最小值。于是，我们直接套用楼房重建线段树的做法即可。
时间复杂度 \(O(n\log^2 n)\)。
记录。
USACO23FEB Watching Cowflix P
做法 1
我们考虑对 \(k\) 根号分治。
对于小于等于根号的部分：我们直接 \(O(n)\) 计算即可。
我们记 \(f_{i,0/1}\) 表示 \(i\) 是否被选，子树内的最小代价，根据儿子是否选来进行转移。
对于大于根号的部分：注意到我们有一种方案是选一个连通块，所有位置全选，这样的代价是 \(n+k\) 的。所以划分的连通块数量不超过根号。于是我们可以求出 \(f_{i,j}\) 表示 \(i\) 子树内被划分成了 \(j\) 个连通块。由于 \(j\) 可以对 \(sz_i\) 取 \(\min\)，所以根据经典的树上背包时间复杂度分析，这部分时间复杂度为 \(O(n\sqrt{n})\)。
总时间复杂度为 \(O(n\sqrt{n})\)。
做法 2
我们考虑对于距离不超过 \(k\) 的两个黑点，肯定是把他们划分成一个连通块最优。注意到这样合并以后，我们对黑点的连通块建虚树，每次的点数是 \(O(\frac{n}{k})\) 的。
所以总点数为 \(O(n\log n)\) 的，于是我们使用做法 1 小于等于根号部分的 \(O(n)\) 暴力。
时间复杂度 \(O(n\log n)\)
POI2014 HOT-Hotels 加强版
ZR 模拟赛的原题，花了点时间过了。
我们考虑长剖，记 \(f_{i,j}\) 表示 \(i\) 子树内距离 \(i\) 为 \(j\) 的点的个数，\(g_{i,j}\) 表示选了两个点，并要求第三个点到 \(i\) 的距离为 \(j\)。
于是我们用长剖优化 DP，转移需要将第二维平移，但 ZR 数据范围 \(10^6\)，我们不可能开 \(10^6\) 个 deque，所以我们用 vector 打个 \(tag\) 即可。
时间复杂度 \(O(n)\)。
记录。
