2023 年 5 月训练记录

[POI2017] Turysta#

学习了竞赛图构造汉密尔顿回路。

首先，竞赛图一定有汉密尔顿路径；其次，强连通竞赛图一定有汉密尔顿回路。

首先对竞赛图缩点，最终拓扑序一定是一条链。考虑如何在一个强连通竞赛图中构造汉密尔顿回路。

首先，我们尝试构造汉密尔顿通路。考虑增量构造。我们一个个地加点，设当前加入的点为 $x$，当前构造好的路径为 $s$ 到 $t$，那么我们分类讨论：

1. 若 $x\to s$，我们直接让 $x$ 连接 $s$，$s:=x$；
2. 若 $t\to x$，我们直接让 $t$ 连接 $x$，$t:=x$；
3. 现在我们只剩下 $s\to x$，$x\to t$ 的情况，于是考虑链上一定存在一个点 $y$ 以及 $y$ 连接的点 $z$，满足 $y\to x$，$x\to z$。于是直接在 $y\to z$ 中插入 $x$ 即可。

考虑多次进行这个过程，每次对点 shuffle，即可获得 $98$ 分，当然这样确实是可以卡的。

接着我们考虑构造汉密尔顿回路。我们依旧考虑增量构造（但不是纯增量构造）。设当前加入的点为 $x$，当前构造好的环起点为 $s$，我们依旧分类讨论：

1. 若 $x\to s$，那么我们直接按照汉密尔顿通路并加入 $x\to s$ 的边即可；
2. 若存在点 $x\to y$，$y$ 在已经构造好的环中，我们找到从 $s$ 开始往后第一个这样的点，设环中 $z\to y$。由于我们找的是第一个，并且 $s\to x$，所以，一定有 $z \to x$。于是就可以构造了。
3. 若不存在情况 2，则我们把这个点留下，并在之后一起构造。

情况 2、3 的构造：

时间复杂度 $O(n^2)$。

记录。

重返现世#

首先，我们上 $min-max$ 容斥，本题求的是第 $k$ 小的期望，我们现把它转化成第 $n-k+1$ 大的期望，下述 $k$ 默认为 $n-k+1$。

$$kthmax(S)=\sum_{\varnothing \ne T \subseteq S} \binom{|T|-1}{k-1} (-1)^{|T|-k} \min(T)$$

证明可以算贡献，首先前 $k-1$ 小的，组合数部分都是 $0$。对于第 $i\ge k$ 大的数，贡献次数为 $\sum\limits_{j=k}^{i}\binom{i-k}{j-k}(-1)^{j-k}$，就是组合数一行奇数列的和 - 偶数列的和，只有在 $i=k$ 为 $1$，其它都恰好抵消，可以通过 $\binom{a}{b}=\binom{a-1}{b-1}+\binom{a-1}{b}$ 来证，而 $\binom{0}{0}$ 是边界。

确定 $T$ 了之后，$min(T)$ 的期望是好算的，直接就是 $\frac{m}{\sum_{i\in T} p_i}$。

然后，由于 $m$ 比较小，我们可以 DP 枚举，注意到这里只有 $\binom{|T|-1}{k-1}$ 是难处理的，我们使用 $\binom{a}{b}=\binom{a-1}{b-1}+\binom{a-1}{b}$，这样我们还得求出对于 $1\le k'\le k$ 处的值。

于是我们 DP，记 $f_{i,j,k}$ 表示前 $i$ 种原料，$\sum_{i\in T} p_i=j$，在 $k$ 处的值。

转移：$f_{i,j,k}=f_{i-1,j,k}+f_{i-1,j - p_i,k-1} +f_{i-1,j - p_i,k}$。

注意点：

1. $min-max$ 容斥，要求 $T\ne \varnothing$。
2. 空间不能直接开，要滚。

时间复杂度 $O(nm(n-k))$

记录。

AGC009D Uninity [POI2004] JAS#

我们把最终分成的 Uninity 值记在每个点上，于是我们就转化成最小化 Uninity 的最大值。

结论：一种 Uninity 填值是否合法，当且仅当任意两个相同 Uninity 路径上，一定存在一个点 Uninity 值大于它们。

然后贪心即可，从叶子往上贪心，每次填能填中间的最小值。

注意到，直接按点分树填值，答案是 $\log$ 的，所以可以用 int 压状态，使用 __builtin 技术即可做到 $O(n)$。

记录。

注意到 JAS 这题本质上与 Uninity 一样。

CF1034D Intervals of Intervals#

我们对于一段第 $[l, r]$ 部分的区间的并，每一段算在最右侧这个部分的区间里面。

那么，每个区间向右能贡献的值，不难发现是一个单调递减的分段函数，由于颜色段均摊，所以，所有区间的总段数 $O(n)$。

于是，我们先跑一遍 ODT，求出这个分段函数。

然后，我们在二分第 $k$ 大，最后再求出前 $k$ 大即可，只需要双指针即可。

时间复杂度 $O(n\log n)$。

记录。

CF1821F Timber#

首先有个 DP，记 $f_{i,j}$ 表示最终从左到右前 $i$ 棵树，最右覆盖到 $j$ 的方案数。

转移：$\begin{cases} 2f_{i,j}\to f_{i+1,j+t}&k+1\le t\le 2k\\f_{i,j}\to f_{i+1,j+t}&t> 2k\end{cases}$。

然后考虑计算 $f_i$ 表示至少 $i$ 次走 $>2k$ 步的方案数，这个是好算的。

之后，我们需要二项式反演，计算出 $g_i$ 表示恰好 $i$ 次走 $>2k$ 步的方案数。

$$g_i=\sum\limits_{j=i}^{m} \binom{j}{i} (-1)^{j-i} f_j$$

答案就是

$$\begin{aligned}& \sum_{i=0}^{m} 2^{m-i} g_i\\ =&\sum_{i=0}^{m} 2^{m-i} \sum_{j=i}^{m}\binom{j}{i} (-1)^{j-i}f_j\\ =&\sum_{i=0}^{m}f_i \sum_{j=0}^{i} \binom{i}{j} 2^{m-j} (-1)^{i-j}\\ =&2^m\sum_{i=0}^{m}f_i \sum_{j=0}^{i} \binom{i}{j} (\frac{1}{2})^{j} (-1)^{i-j}\\ =&2^m\sum_{i=0}^{m}f_i (-\frac{1}{2})^i\\ \end{aligned}$$

时间复杂度 $O(n)$。

记录。

[NOI2020] 命运#

感觉代码比 生日蛋糕 简单很多。

首先有个 DP，记 $f_{i,j}$ 表示到 $i$ 号点，向上最远覆盖到 $j$，然后转移用线段树合并下就没了。

时间复杂度 $O(n\log m)$。

记录。

AGC016F Games on DAG#

很神秘的题。

首先，先手必胜当且仅当 $SG(1)\ne SG(2)$，那么我们容斥下，计算 $SG(1)=SG(2)$ 的方案数。

考虑 $mex$ 这东西，正过来从小往大枚举层很难做，要对于当前层的每个点都在前面所有层至少有一条连边。但是我们倒过来做，就豁然开朗了，我们只需要保证前面所有点都至少跟当前层的一个点有连边。

于是我们 DP，记 $f_i$ 已经确定 SG 函数值的方案数。

转移就枚举下一层 SG 函数的集合。

直接做复杂度是 $O(3^n n)$ 的，稍微观察下即可优化成 $O(3^n)$。

记录。

基础数论函数练习题#

我们考虑对质因子算贡献，对于重复部分统计在最右侧。

这样右移右端点到 $j$，令 $t=a_j$，再从右往左扫到 $i$，计算出 $g = \gcd(t,a_i)$，然后 $t:=\frac{t}{g}$，$a_i:=\frac{a_i}{g}$，$ans_{i,j}=\prod\limits_{k=i}^{j} a_k$。

时间复杂度 $O(Tn^2 \log)$，是不能通过的，不过计算 $\gcd(x,y)$ 时通过特判 $x,y=1$ 减枝可以 1.98s 卡过去，喜提最劣解。

考虑优化这个做法，我们发现确定右端点后一轮，$t$ 只会变化 $log$ 次，而我们求了 $n$ 次 $\gcd$，这明显不优。

我们观察上述算法的过程，注意到左端点移动到 $i$ 时，$t$ 的值实际上是 $\frac{a_j}{\gcd(a_j,\prod\limits_{k=i+1}^{j-1} a_k)}$。

那么，$a_i$ 值有变化当且仅当 $\gcd(a_j,\prod\limits_{k=i+1}^{j-1} a_k)\ne \gcd(a_j,\prod\limits_{k=i}^{j-1} a_k)$。

然后注意到由于辗转相减法，所有 $a_i$ 值有变化当且仅当 $\gcd(a_j,\prod\limits_{k=i+1}^{j-1} a_k \bmod a_j)\ne \gcd(a_j,\prod\limits_{k=i}^{j-1} a_k \bmod a_j)$。

时间复杂度 $O(Tn^2)$。

记录。

CF1687C Sanae and Giant Robot#

VP 时写了个假做法，比赛结束跟题解对拍才意识到假了。。。

首先，将 $a_i$ 与 $b_i$ 对位减，一次操作就相当于把一段和为 $0$ 的全部替换为 $0$。

然后考虑前缀和，一次操作就相当于将两个相同的数，中间全部替换成这个数。注意到如果这个数不为 $0$，这次操作肯定不优，所以我们每次找 $0$ 的操作来做，用 set 维护下连续段即可。

时间复杂度 $O(m\log n)$。

记录。

CF1687D Cute number#

首先，$[k^2,k^2+k]$ 中的数会被认为合法。

我们枚举 $a_1$ 最终所在的 $k$，因为 $k=a_n$ 必然可行，所以最多只有 $2e6$ 种，主要到对于后面的数，合法段与非法段的差一定大于等于 $k$，所以差小于等于 $k$ 的数一定所在 $k$ 相同。

于是就可以每次暴力扫所有段，并求解。

时间复杂度 $O(n\log a)$。

记录。

PR8B 消愁 QOJ1839 Joke#

首先，$p,q$ 只依赖于 $(p_i,q_i)$ 的大小关系，所以，不妨先把 $p_i$ 调整成 $1\sim n$。

有个强大结论：$f((1,2,\cdots,n),q)=$ $q$ 的递增子序列的个数。

证明：我们现按照 $p,q$ 大小关系连边，则一种正确的填法需要保证不出现环，我们考虑按照 $q_i={1,2,3,\cdots,n}$ 的位置来填，假设当前填 $i$，注意到如果当前选择了 $p_i>q_i$ 则 $i$ 左侧未填的一定要填 $p_i>q_i$。

所以，填 $p_i>q_i$ 的位置构成递增子序列，于是现在问题转化成求递增子序列的个数。

我们记 $f_{i,j}$ 表示到第 $i$ 个位置，递增自序列最后一个在 $q$ 中非 $0$ 的位置为 $j$ 的方案数。

时间复杂度 $O(n^4)$。

记录。

CF1264D Beautiful Bracket Sequence#

计数这个东西有两种方法：

1. 计算答案 $\ge k$ 的方案数，枚举第 $k$ 个 ( 的位置，计算下方案数；
2. 注意到一个序列一定恰好有一个位置满足这个位置是 (，并且它左侧（包含它）的 ( 个数等于它右侧 ) 的个数。

这 2 种方法推出的柿子稍微化一下就一样了。以第 2 种为例：

记 $S1_i$ 表示 $i$ 左侧（包含 $i$）的 ( 个数，$S2_i$ 表示 $i$ 左侧（包含 $i$）的 ? 个数，$S3_i$ 表示 $i$ 右侧（不包含 $i$）的 ( 个数，$S4_i$ 表示 $i$ 右侧（不包含 $i$）的 ? 个数，

$$\begin{aligned} &\sum_{st_i\ne ')'}\sum_{j} j\binom{S2_i}{j-S1_i} \binom{S4_i}{j-S3_i}\\ =&\sum_{st_i\ne ')'}\sum_{j} (j-S1_i)\binom{S2_i}{j-S1_i} \binom{S4_i}{j-S3_i}-S1_i\sum_{j}\binom{S2_i}{j-S1_i} \binom{S4_i}{j-S3_i}\\ =&\sum_{st_i\ne ')'}\sum_{j} (j-S1_i)\binom{S2_i}{j-S1_i} \binom{S4_i}{S4_i+S3_i-j}-S1_i\sum_{j}\binom{S2_i}{j-S1_i} \binom{S4_i}{S4_i+S3_i-j}\\ =&\sum_{st_i\ne ')'}S2_i\sum_{j} \binom{S2_i-1}{j-S1_i-1} \binom{S4_i}{S4_i+S3_i-j}-S1_i\sum_{j}\binom{S2_i}{j-S1_i} \binom{S4_i}{S4_i+S3_i-j}\\ =&\sum_{st_i\ne ')'}S2_i \binom{S2_i-1+S4_i}{j+S1_i-1+j-S3_i}-S1_i\binom{S2_i+S4_i}{j-S1_i+S4_i+S3_i-j} \\ \end{aligned}$$

倒数第 2 步是吸收恒等式，最后一步是范德蒙德卷积。

时间复杂度 $O(n)$。

记录。

[SHOI2006] 有色图#

首先上 Pólya。

观察数据范围，发现可以拆分数地枚举所以置换环大小。

我们令所有置换环长度为 $len_1,len_2,\cdots,len_k$，则对应的划分方案数为 $\binom{n}{len_1,len_2,\cdots,len_k}$，由于一个环内可以换，所以还要乘 $\prod_{i=1}^{k} (len_i-1)!$。但这还有一个问题，对于 $len$ 相同的环，顺序改变会被算作不同方案。

所以，置换环的方案数为 $\frac{1}{\prod_i c_i!}\frac{n}{\prod_{i=1}^{k}len_i!}\prod_{i=1}^{k} (len_i-1)!=\frac{n}{\prod c_i! \prod_{i=1}^{k}len_i}$。

之后再求不相交的循环置换的数量。首先是同一个置换环中，有 $\lfloor\frac{len_i}{2}\rfloor$ 种等价类；在不同置换环中，首先每条边属于一个 $\text{lcm}(len_i,len_j)$ 大小的等价类中，所以等价类个数为 $\frac{len_ilen_j}{\text{lcm}(len_i, len_j)}=\gcd(len_i,len_j)$ 个。

记录。

CF1608F MEX counting#

DP，我们设 $f_{i,j,k}$ 为前 $i$ 个数，$mex$ 为 $j$，有 $k$ 种不同的数 $>j$。

我们这么设状态的目的，是如果不设为不同，那么转移必然避免不了枚举一种值出现的次数 $t$，而 $\binom{k}{t}$ 是不好拆的。

这么设状态就好做了，我们分 $4$ 类写转移：

1. $a_{i+1}<j$；
2. $a_{i+1}=j$；
3. $a_{i+1}>j$，跟前面 $k$ 种存在相同；
4. $a_{i+1}>j$，跟前面 $k$ 种不存在相同；

时间复杂度 $O(n^2k)$。

记录。

[PA2019] Podatki drogowe#

yaoyi /cf

做法是首先跑一遍边分治，用主席树维护到两端点的路径。

求第 $k$ 大我们考虑二分，这里值域是 $n^n$ 级别，但路径个数是 $n^2$ 级别，所以我们考虑随机二分。

判断两条路径的大小关系之间在主席树上二分下即可。

时间复杂度 $O(n\log^3 n)$。

说的很简单，写起来就不一样了。。。

不过这题十分良心，不卡常，时限 $5s$，最满的点 $2s$ 就过了，@kyEEcccccc，一个不是最大的点跑了 $>40s$，但他坚称他写的是 $log^3$。

记录。

CF1728F Fishermen#

由于可以重排，所以严格单调等价于原始时互不相同，然后考虑建出二分图，左侧 $i$ 向右侧 $a_i,2a_i,\cdots,na_i$ 连边，跑二分图最小权完美匹配。

注意到左侧点个数为 $n$，我们在右侧从小往大跑匈牙利，并且在没有匹配的情况下不清空 vis 数组可以将算法复杂度优化到 $O(n^3)$。

记录。

[USACO20OPEN] Exercise P#

很强大的题。首先一个排列的步数为所有置换环长度的 $lcm$。

接着，我们考虑如何计算答案。类似于把求恰好转化为求大于等于的思想，我们对质因子这么算，于是答案为 $\prod_p p^{\sum_c F(p^c)}$，其中 $F(x)$ 表示 $x|lcm$ 的方案数。

我们考虑如何计算 $F(x)$，因为是 $lcm$，只要有一个被 $x$ 整除即可，这不太好处理，所以我们记 $f_i$ 表示总大小为 $i$，且所有置换环都不被 $x$ 整除的方案数，为了算这个我们记 $g_i$ 表示总大小为 $i$，且所有置换环都被 $x$ 整除的方案数。

那么，$f_i$ 容斥算。

$$f_i=i!-\sum\limits_{x|j,j\le i} g_jf_{i-j}$$

而 $g_i$ 可以通过枚举 $1$ 所在的置换环大小来算，需要乘组合数和圆排列方案数。

$$g_i=\sum_{x|j,j\le i}\binom{i-1}{j-1} (j-1)! g_{i-j}$$

注意到 $g_i$ 有值当前仅当 $x|i$，而 $f_i$ 能对 $f_n$ 产生贡献当且仅当 $i\equiv n\pmod x$。

所以，计算 $F(x)$ 的复杂度为 $O((\frac{n}{x})^2)$。

时间复杂度为：

$$\frac{n^2}{4}\le\sum_{i=1}^{n}[\omega(i)=1] (\frac{n}{i})^2\le \sum_{i=1}^{n} (\frac{n}{i})^2=n^2\sum_{i=1}^{n} \frac{1}{i^2}$$

根据巴塞尔问题的结论，$\lim(1+\frac{1}{4}+\frac{1}{9}+\cdots)=\frac{\pi ^ 2}{6}$，是 $\Theta(1)$ 的。

所以，时间复杂度为 $\theta(n^2)$。

记录。

[省选联考 2023] 过河卒#

状态是 $2n^6$ 的，注意到有环依旧可以做。

先把所有状态搜出了，然后 BFS，从必胜、比败按步数往前搜。若是必败往前，则直接松弛；若所有出边都是必胜状态，则选择步数最多的状态松弛。否则没有被更新，说明有环，答案为 Tie。

时间复杂度 $O(Tn^6)$。

记录。

LaLa and Divination Magic#

根 ybw 打 Universal Cup，本着计算几何狗都不做的策略，ybw 开了 C，我开了 G。

结果我 G 一直 T，又不太会优化，后来看到 ybw 不会 C 摆了就也摆了。于是我们队 0 题。

我的做法烦了，我先找出了所以可行的 2-SAT 对，然后跑了遍 2-SAT，缩点。

若一个点可以到另一个点，则若前者为 true，则后者一定为 true。

最后按照了强连通分量的拓扑序 DFS 找可行解。

但实际上可以按照编号来搜，这样就不会有非法方案了。

中间求 DAG 可达可以用 bitset 优化，DFS 也可以用 bitset 优化。

事实上不需要真的跑 2-SAT，直接做就行了。。。

时间复杂度 $O(\frac{n^3}{w})$。

记录。

Qk1E Quark and Game#

考虑一个数通过 $x$ 次 1 操作，再做 $1$ 次 2 操作，再来做 $1$ 次 1 操作，仍然可以操作的 $x$ 只有 $1$ 种。

于是，我们对于每个 $i$，把这样的 $x$ 建成字典树，然后在字典树上 DP，然后对于没有出现过的 $x$，一定只会去选择第一个，因为能直接通过 $1$ 次 2 操作，再来做 $1$ 次 1 操作就做完了。

时间复杂度 $O(n\log n)$，我写丑了，写了 $O(n\log ^2 n)$。

记录。

手势密码#

线性规划，考虑一条路径 $s$ 令其出现次数为 $c_s$。

则需要满足：

$$\min \sum_{s} x_s$$

$$\begin{cases} \sum_{s\ni i} x_s=a_i\\ x_s\ge 0 \end{cases}$$

转化成线性规划的形式：

$$\begin{cases} \sum_{s\ni i} x_s\ge a_i\\ \sum_{s\ni i} -x_s\ge -a_i\\ x_s\ge 0 \end{cases}$$

转对偶：

$$\max \sum_{i} a_i(s_i-t_i)$$

$$\begin{cases} \sum_{i\ni s} a_i(s_i-t_i)\le 1\\ s_i,t_i\ge 0 \end{cases}$$

然后树形 DP，注意到 $s_i-t_i\in {-1, 0, 1}$，于是 $f_{i,j}$ 表示 $i$ 子树内，最长路径为 $j$ 的方案数，$j\in {0,1}$。

时间复杂度 $O(n)$。

记录。

[ZJOI2020] 序列#

一个非常高妙的贪心做法。我们从左往右扫，假设当前操作 $i$，若 $a_{i+1}\ne 0$，就用直线，否则再用跳线。

1. 如果 $a_{i+1}$ 用直线，则改称从 $i$ 开始直线，从 $i+3$ 开始跳线一定不劣；
2. 如果 $a_{i+1}$ 用跳线，考虑 $i$、$i+1$ 开始的两条跳线一定一段连续区间，不如用直线。

如果前面的线使得 $a_{i+1}$ 会减到小于 $0$，可以维护值表示自由线段数量即可。

时间复杂度 $O(n)$。

记录。

AGC005F Many Easy Problems#

首先我们对每个点计算答案，我们发现一个点不在最小连通块中当且仅当点集中的点全在一棵子树中。我们计算 $f_i$ 表示大小为 $i$ 的对于所有大小为 $i$ 的点集，求出能够包含它的最小连通块不包括的点的个数。

最后答案就是 $n\binom{n}{i}-f_i$。

现在考虑计算 $f_i$，观察下即可发现在解决这样一个问题：

多次操作，每次对于一个长度为 $k$ 的前缀，对位加第 $k$ 行组合数。最后求所有位置的值。

这就相当于多次加入 $(x+1)^k$，最后求 $[x^i]$，直接多项式平移即可。

时间复杂度 $O(n\log n)$。

记录。

雅礼集训 2017 Day11 PATH#

考虑在每个格子填第一次出现的时间，于是就变成了求它是杨表的概率。

首先计算总方案数，为 $\binom{\sum_{i=1}^{n} a_i}{a_1, a_2, \cdots, a_n}$ 即 $\frac{(\sum_{i=1}^{n} a_i)!}{\prod_{i=1}^{n} a_i!}$。

然后是杨表个数，根据论文，令 $b_i=a_i+n-i$ 得到 $\frac{(\sum_{i=1}^{n} a_i)!\prod_{1\le i < j\le n}(b_i-b_j)}{\prod_{i=1}^{n} b_i!}$。

所以答案为

$$\frac{\frac{(\sum_{i=1}^{n} a_i)!\prod_{1\le i < j\le n}(b_i-b_j)}{\prod_{i=1}^{n} b_i!}}{\frac{(\sum_{i=1}^{n} a_i)!}{\prod_{i=1}^{n} a_i!}}= \frac{\prod_{1\le i < j\le n}(b_i-b_j)\prod_{i=1}^{n} a_i!}{\prod_{i=1}^{n} b_i!}$$

现在问题就是求 $\prod_{1\le i < j\le n}(b_i-b_j)$，注意到 $b_i$ 单调递减，所以直接形式幂级数，然后求 $> 0$ 次的系数即可。

记录。

count#

zyx /bx

首先 $m>n$ 时，答案是 $0$。

现在就只剩下 $m\le n$ 的情况了，注意到答案相当于是在对 $f$ 的种类计数。我们先对答案序列建出笛卡尔树（根题目一样，如果有多个最大值，取下标最小的），这样我们就能确定所有 $f(l,r)$ 的值了。考虑什么样的笛卡尔树不合法，注意到一个事情：假设我们现在笛卡尔树一个点对应的区间是 $[l,r]$，最大值所在的点为 $mid$，则 $a_{[l,mid-1]}$ 中要严格小于 $a_{mid}$，而 $a_{[mid+1,r]}$ 中只要小于等于 $a_{mid}$。

所以 $m$ 的限制相当于要求笛卡尔树的根到每个点上左儿子数量 $<m$。

于是，现在问题转化为：

计数 $n$ 个点的二叉树，要求根到每个点上左儿子数量 $<m$。

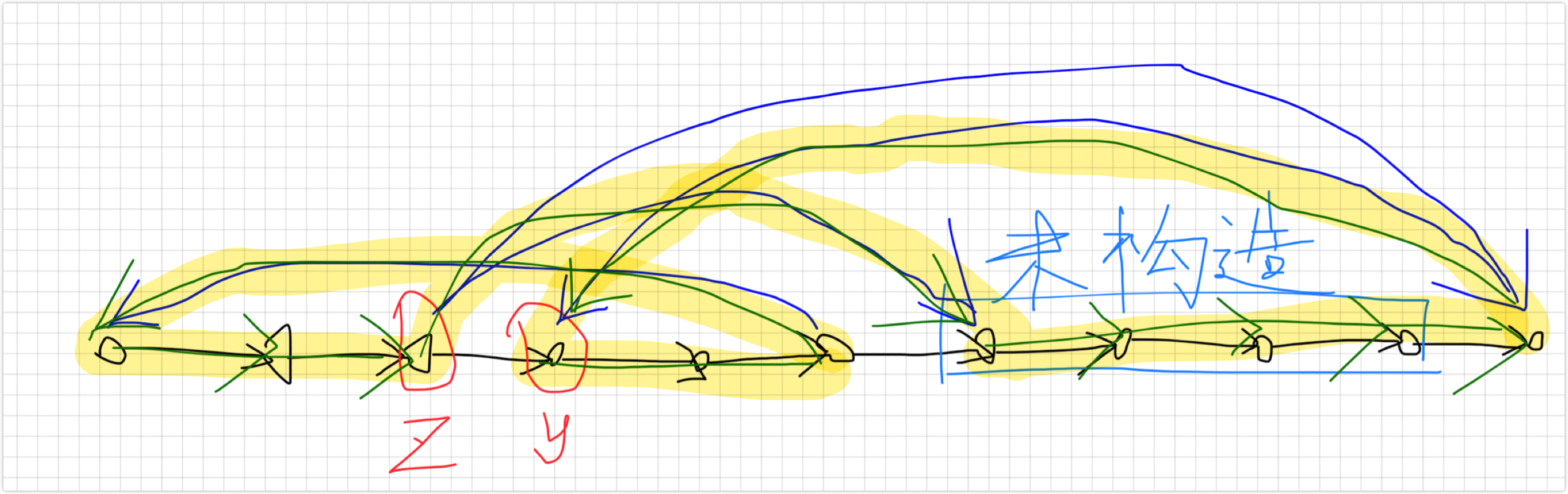
考虑一个非常神仙的做法：

我们将 $n$ 个点的区分左右儿子的二叉树转换成 $n+1$ 个点的普通树。

具体地，我们先设一个虚根，然后对于从根出发连续向右的链，我们全接在虚根上。

对于从根出发连续向右的链上的每个点，我们对于它的左子树，以它为虚根递归构造。

下图是一个例子：

注意到对于普通树，我们有一个经典做法：转化成括号序。

对于上面要求根到每个点上左儿子数量 $<m$ 的限制，在普通树上就变成了每个点的深度 $\le m$，在括号序上就变成了前缀函数 $\le m$。

于是现在，我们相当于有一个函数 $f(x)$，每次 $f(x)=$ $f(x-1)-1$ 或 $f(x-1)+1$，并且要求不能碰到 $y=-1$ 和 $y=m+1$ 两条线。

这又有一个经典做法：

据卷王 zyx 说，这个问题就是 [JLOI2015] 骗我呢。

我们容斥，减去经过 $y=m$ 和 $y=-1$ 的方案数，加上先经过 $y=m$ 再经过 $y=-1$ 和先经过 $y=-1$ 再经过 $y=m$ 的方案数……

相当于对终点不断地翻折。

时间复杂度 $O(n)$。

记录。

[JLOI2015] 骗我呢#

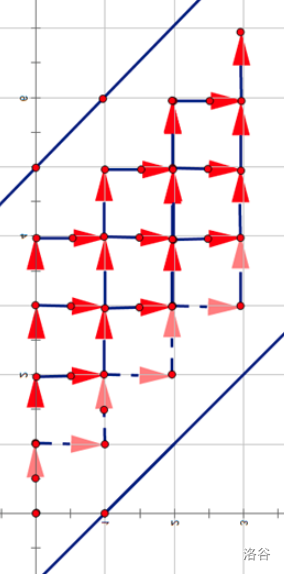
记 $x_i$ 中没有出现的值为 $a_i$，则要求 $0\le a_i\le m$，并且 $a_{i-1}-1\le a_i$。

把它画出来就是这样：

然后考虑拉伸：

唯一难处理的直角三角形，我们加一个点就行了。

于是就变成了上面的那个套路。

时间复杂度 $O(n)$。

记录。

Forestry#

最近看到挺多人的做题记录写到了这题，以为是好题，不过看了下发现是烂题。

见了多少遍的套路：

1. [PKUWC2018]Minimax；
2. 生日蛋糕；
3. SD 集训 Qingyu 搬了生日蛋糕；
4. [NOI2020] 命运。

我这么摆、做题量这么小的人能见这么多遍，属实罕见。从第一遍做 Minimax 觉得新奇，到生日蛋糕整场调不出来，再到觉得套路。

这类题目的套路就是树型 DP，儿子向父亲转移时带 $min$ 或者 $max$，这在线段树合并是相当好处理的。

这类题目的难点在于 lazy_tag，要想清楚如何合并 tag，否则就会模拟赛一整场调不出来，具体可以看 生日蛋糕的 blog。

记录。

LGR139D 似曾相识燕归来#

首先观察到，把 $1$ 换到首位后，后面就可以随便换了。而后面换的次数为 $n-1-$ 置换环个数。

那么我们大力分讨：

首先，我们令 $q_i$ 表示 $i$ 在排列 $p$ 中的出现位置，那么我们

1. $q_1=n$：$1$ 动不了，显然无解；
2. $q_1=1$：直接对后面的数交换；
3. $\exists i q_1<i\le n, p_i<p_1$：对 $(1,i,q_1)$ 操作，转化成了 $case 2$，操作次数最大为 $1+n-1-1=n-1$。
4. $p_1\ge 3$：由于我们判掉了 $case\ 3$，于是 $q_1$ 右侧就全都是 $>p_1$ 的数了，所以 $<p_1$ 的数一定全在 $i$ 左侧，又因为 $p_1\ge 3$，所以一定 $i$ 左侧一定存在 $i$，满足 $1<i<q_1$ 并且 $p_i<p_1$。于是，先多 $(1, i, n)$ 操作，这样就转化成 $case 3$ 了，操作次数最大为 $1+n-1=n$。
5. $p_1=2,p_2=1$：
   1. $p_i=i(i>2)$：这种情况我们对 $(1, 2, 3)$ 操作，转化成 $case\ 4$，然后注意到由于 $p_i=i$，所以我们的操作次数固定为 $5$，所以 $n=L=4$ 无解；
   2. 否则一定能找到一个位置 $i$ 满足 $2<i<n$ 且 $p_i>p_{i+1}$。然后我们操作 $(1,2,i)$，$(1,2,i)$，这样就能转化成 $case\ 3$ 的情况，注意到这 $2$ 次操作结束后 $p_2=2$，所以操作次数最大为 $2+((n-1)-1)=n$。

时间复杂度 $O(n)$。

记录。

CF512D Fox And Travelling#

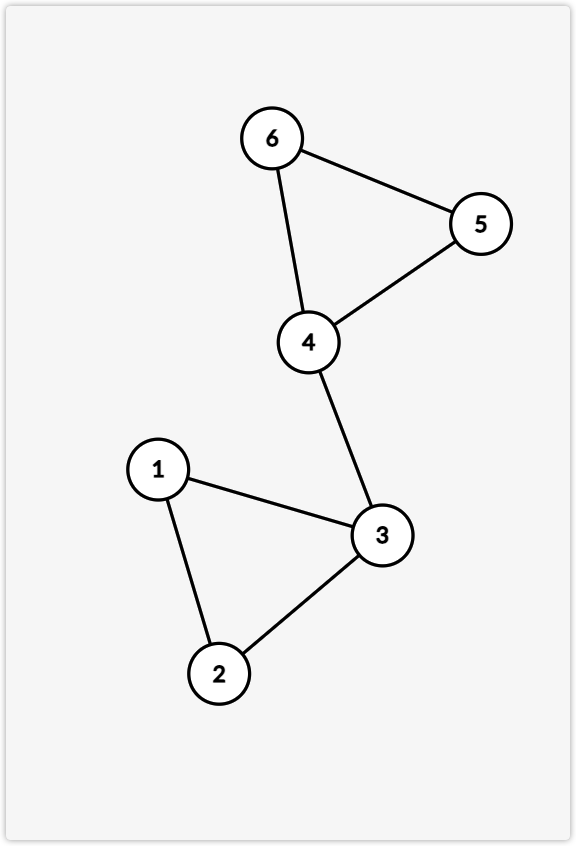
这个题首先考虑环上的点一定不会被删，但这个结论太弱了，就比如说：

我们考虑直接模拟删点的过程，我们先把度数 $\le 1$ 的点加入队列，然后类似拓扑排序地做，这样就可以找到所以可以删的点了，这些点一定形成森林。

由于度数为 $1$ 的限制，每棵树最多有一个点可能与不可删的点有连边。下面分有和没有分类讨论：

1. 有：

   这样每个点需要被删前就确定了要删那些点，我们以那个点为根，跑一遍树形 DP，求出答案。

2. 没有：

   我们枚举最后一个被删的点，然后以每个点为根跑 $1$ 的算法，当前这样会算重，注意到我们删一个连通块会被任何不在这个连通块上的点统计到，于是除一下就好了。

注意到森林中的每棵树是独立的，所以做一遍加法卷积就行了。

记录。

CF1738G Anti-Increasing Addicts#

Anton /bx

很高妙的题。

首先，根据 Dilworth 引理，最长反链 = 最小链覆盖。

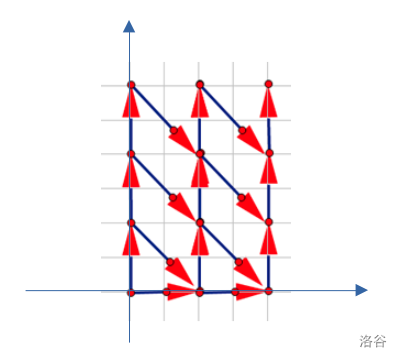
那么也就是要求构造解使得最小连覆 $<k$。注意到这个限制是紧的，因为 $k-1$ 条链最多只能覆盖 $n^2-(n-k)^2$ 个点（每个点只和它上、右右边）。

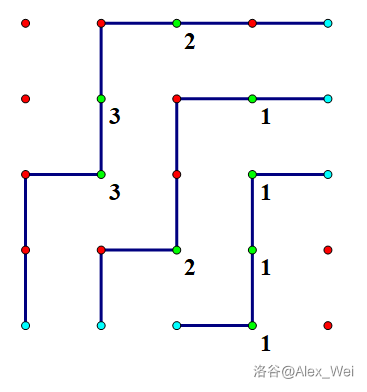
这里偷一张魏老师的图：

所以，为了满足这个限制，我们需要让第 $i$ 条链从 $(n,k-i)$ 出发，在 $(k-i,n)$ 结束。

然后考虑题目有些点被删选的限制，就相当于有些点不能被覆盖。首先考虑无解的情况，可以证明无解当且仅当不能删的点构成长度为 $k$ 的链。充分性显然，必要性考虑多不存在长度为 $k$ 的链的情况进行构造。我们令 $f_{i,j}$ 表示以第 $i$ 行第 $j$ 列这个位置结尾的最长链。我们按 $f_{i,j}$ 分层，我们让值为 $i$ 的被第 $i$ 条链覆盖。

由于 $f_{i,j}$ 的性质，构成二维偏序，所以我们一定能构造出来。具体构造时，我们贪心，能向上就向上，否则再向右。

时间复杂度 $O(n^2)$。

记录。

CF576E Painting Edges#

注意到这题与这题很像，我们用类似的方法来处理。

首先，这道题的不一样之处在于若操作不合法就不操作，那么我们可以看成对于不执行的操作，我们染与之前一样的颜色。

于是，我们依旧线段数分治，在叶子处判断这次操作是否执行，然后递归到别的节点的时候判断操作的颜色。

时间复杂度 $O(q\log q\log n)$，分别是线段数分治和可撤销并查集的 $\log$。

记录。

CF576D Flights for Regular Customers#

模拟赛做过这题的无向图版本，不过大不一样，那题可以出到 $5\times 10^5$，做到 $O(m \log n)$，做法：

由于是无向图，所以我们可以在一条边上来回移动，浪费时间，所以到达一条边的一个端点肯定是越早越好，于是分在哪条边上，哪个端点，以及长度的奇偶性来设状态 $f_{i,0/1,0/1}$。然后跑 dij 即可。

模拟赛时，我 $n=1$ 会判断为无解，结果那题打包，而且每个包都放 $n=1$ 的测试点，不过还好最后评测的时候把包拆了，不然真就保龄了。。。

再来看这个题，注意到 $n,m$ 很小，我们按照边出现的时间段划分，先通过矩阵乘法来维护每段时间内哪些点可到，然后再 BFS，求出最短路。

直接做时间复杂度为 $O(n^3m\log d)$，不能通过。

注意到维护每段时间内哪些点可到可以将矩阵转置，并用 bitset 优化。

时间复杂度 $O(\frac{n^3m\log d}{\omega})$。

记录。

ARC096E Everything on It#

首先考虑容斥，我们钦定出现 $0$ 次的数个数为 $a$，出现 $1$ 次的数个数为 $b$，对应的容斥系数为 $(-1)^{a+b}$。计算其方案数需要再枚举出现次数为 $1$ 的数在 $c$ 个集合中，所以方案数为 $\binom{n}{a}\binom{n-a}{b}\begin{Bmatrix}b\\ c\end{Bmatrix}2^{2^{n-a-b}}(2^{n-a-b})^{c}$。

所以，总答案为：

$$\sum_{a=0}^{n}\binom{n}{a}\sum_{b=0}^{n-a}\binom{n-a}{b}\sum_{c=0}^{b}\begin{Bmatrix}b\\ c\end{Bmatrix}2^{2^{n-a-b}}(2^{n-a-b})^{c}$$

这样计算是 3 方的，注意到 $2^{2^{n-a-b}}(2^{n-a-b})^{c}$ 只和 $a+b$ 和 $c$ 有关。

我们考虑在前面优化，我们考虑组合意义，令 $s=a+b$。

$$\sum_{a=0}^{n}\binom{n}{a}\sum_{b=0}^{n-a}\binom{n-a}{b}\sum_{c=0}^{b}\begin{Bmatrix}b\\ c\end{Bmatrix}=\sum_{s=0}^{n}\binom{n}{s}\sum_{c=0}^{s}\begin{Bmatrix}s+1\\ c+1\end{Bmatrix}$$

其中，$\begin{Bmatrix}s+1\\ c+1\end{Bmatrix}$ 的组合意义：我们新增一个数、新增一个集合来“占位”，表示垃圾桶，而在这里面的元素则表示没有出现。

非常高妙。

于是就可以平方计算了。

$$\sum_{s=0}^{n}\binom{n}{s}\sum_{c=0}^{s}\begin{Bmatrix}s+1\\ c+1\end{Bmatrix}2^{2^{n-s}}(2^{n-s})^{c}$$

时间复杂度 $O(n^2)$。

记录。

AGC059C Guessing Permutation for as Long as Possible#

首先有个结论是一个排列合法当且仅当不存在三元组非法。

必要性显然。充分性考虑如果存在 $p_1,p_2,\cdots,p_n(n>3)$ 非法，那考虑任意不相邻的两个点之间边的方向，无论怎么连都会出现一个更小的环，如此下去，一定会划分出大小为 $3$ 的环。

于是，我们枚举三元组，并对两个点的大小关系为点建 2-SAT 图，注意到由于是无向图，所以答案为 $2^{\frac{连通块个数}{2}}$。

时间复杂度 $O(n^3)$。

记录。

AGC062C Mex of Subset Sum#

场上过了评分更高的 B，却没有过评分更低的 C，不过感觉这 C 其实也不简单啊。

我们先将数从小到大排序，然后从左往右扫。

假设当前扫到 $i$，令 $sum=\sum\limits_{j=1}^{i-1} a_j$，维护集合 $cur_{i-1}$ 表示在 $[1,sum]$ 中无法被前 $i-1$ 个数表示的数。

若 $cur$ 中 $<a_{i}$ 的数的个数 $\ge k$，则停止。

否则分类讨论：

1. $sum < a_i$：则新增无法表示的数 $(sum,a_i)$，以及 $\forall j\in cur_{i-1}, j+a_i$；
2. $sum\ge a_i$：则 $cur_i$ 中的数 $j$ 需满足不管用不用 $a_i$ 都无法凑出。
   不用 $a_i$ 无法凑出有两种可能：
   1. $j>sum$；
   2. $j\in cur_{i-1}$。
   用 $a_i$ 无法凑出有两种可能：
   1. $j<a_i$；
   2. $j-a_i\in cur_{i-1}$。
   于是根据上面的情况组合起来，可以得到 $j\in cur_{i}$ 当且仅当下列任意一个条件满足：
   1. $j\in cur_{i-1} \land j<a_i$；
   2. $j\in cur_{i-1} \land j-a_i\in cur_{i-1}$；
   3. $j>sum \land j-a_i\in cur_{i-1}$。

时间复杂度 $O(n^2k\log(nk))$。

记录。

[NOI2013] 向量内积#

很神仙。

我们设原 $n\times d$ 的矩阵为 $A$，则 $(A\times B)_{i,j}$ 为向量 $i$ 和 $j$ 的内积。

首先考虑 $k=2$，那么现在我们相当于要判断 $A\times A^T$ 是否为全 $1$ 矩阵（不考虑对角线）。

这是个经典问题，GDKOI2023 Day1 T1，我现场就只有暴力分。。。

做法是随一个长度为 $n$ 的向量去乘，判断乘完的向量是否一样，每次错误率为 $\frac{1}{k}$，随 $20\sim 30$ 次就可以保证正确。

时间复杂度 $O(nd)$。

接下来考虑 $k=3$。首先注意到 $1^2\equiv 2^2\equiv 1\pmod 3$。于是只需要判断 $(A\times A^T)^2$ 是否全为 $1$ 即可（依旧不考虑对角线）。

我们沿用上面随向量的方法。设 $B=A\times A^T$，随的向量为 $r$，则我们可以令 $R$ 为只有对角线有值，$R_{i,i}=r_i$ 的 $n\times n$ 矩阵，由于 $(B\times R\times B)_{i,i}=\sum\limits_{j=1}^{n}B_{j,i}R_{i,i}B_{i,j}$。

注意到显然 $B_{i,j}=B_{j,i}$，所以 $B=B^T$。

所以，我们只需要计算 $B\times R\times B=(A\times A^T)\times R \times (A\times A^T)=A\times (A^T\times R\times A) \times A^T$。

由于 $R$ 只有对角线有值，且最后只关心对角线上的值，所以时间复杂度为 $O(nd^2)$。

记录。

COT3 Combat on a tree#

注意到选择一个点后，相当于分裂出了一些独立的子树。

于是我们考虑维护每课子树的 $SG$ 值，我们对一个子树内的所有 $SG$ 值建成 Trie，需要维护整体异或（打 tag），求 $mex$（Trie 上二分）即可。

时间复杂度 $O(n\log n)$。

记录。

AGC043D Merge Triplets#

一道非常 AGC 的 AGC 题，我们考虑找充要条件。

首先，我们注意到如果一个段出现了递减段，那么说明选了前面的后，后面的一定会立即结在后面选，于是最终序列所有递减段长度 $\le 3$。

注意到一个长度为 $3$ 的序列可能有 $3$ 种贡献方式：

1. $1$ 个长度为 $3$ 的递减段；
2. $1$ 个长度为 $1$ 的递减段，$1$ 个长度为 $2$ 的递减段；
3. $3$ 个长度为 $1$ 的递减段。

于是，我们发现需要满足长度为 $2$ 的递减段个数 $\le$ 长度为 $1$ 的递减段个数。

必要性显然，充分性考虑构造：长度为 $3$ 的单独构成，假设剩下 $a$ 个长度为 $1$ 的递减段、$a$ 个长度为 $1$ 的递减段，$b$ 个长度为 $2$ 的递减段，则说明 $a+2b\equiv 0 \pmod 3$，所以 $a-b\equiv 0\pmod 3$，所以一定存在长度为 $2$ 的递减段去和长度为 $1$ 的递减段匹配，再将剩下的长度为 $1$ 的递减段每 $3$ 个划一组的方案。

时间复杂度 $O(n^2)$。

记录。