2023 年 4 月训练记录

训练

省选后先学了一段时间的 whk。

[省选联考 2023] 填数游戏

zyx /bx

首先，对 \(B\) 能选的两个数连边（\(|t_i|=1\) 看作连一条自环）。

考虑如果一个连通块的边数 > 点数，那一定没有完美匹配，无解。于是，现在只剩下边数 = 点数（基环树），边数 < 点数（树）

基环树的情况是好做的，树边方向是确定的；而环上的边只有两种情况。讨论一下，即可得到答案。

而树的情况相对复杂一些。

首先，先随便拉一个点做根。可以观察到 B 的操作一定是以一个点为根的外向树来定边的方向。若 A 选择限制一条边的父亲，那么子树内的点做根的代价就将增加 \(1\)，若 A 选择限制一条边的儿子，那么子树外的点做根的代价就将增加 \(1\)。

如果一条边小 A 啥都不能限制，那就忽略即可；如果只能限制一个点，那就直接树上差分。

剩下部分有非常多种，这里记录了我现在所知道的 3 种做法：

1. 考虑调整法手玩可以证明，小 A 对两个端点都能定向的边，一定是按照一个点为根的内向树来定边的方向。

   于是考虑 dfs，换根来计算答案。从根到儿子需要改变一条边的方向，于是只需要线段树维护区间加，全局最小值即可，\(O(n\log n)\)。

2. 考虑先让这些边都选择的边都选择子树内加 1，这样每次调整相当于全局加 1，子树内减 2。考虑在一个点更改选择，一定不优于在子树内更改答案。于是，更改选择的点一定是若干棵不交子树。

   考虑先计算 \(f_i\) 表示，对 \(i\) 子树内操作后子树内的最小值。对 \(f_i\) 排序，最后答案一定是对排序后前缀的子树操作，\(O(n \log n)\)。

3. 我的假做法 /kk：考虑不在子树内最小值不会改变子树内的值和全局最小值的相对大小。开始以为更改选择不会改变全局最小值的位置，后来发现可以进行操作使全局最小值变小（不算全局加 1），但增加别的点的值。这就涉及到排序的问题，试了几种排序都假了 /kk。

   于是考虑人类智慧，我们感觉最后的全局最小值不会变小太多。另这个值为 \(c\)。当 \(c\) 取到 \(5\) 时就能有 76 分的优异成绩了，取到 \(6\) 时就 96 分了，取到 \(7\) 以上就 100 分了，\(O(cn)\)。

   假做法 link：https://loj.ac/s/1752346。

   目前还不知道咋卡，有人知道可以来恭喜我下）。

[省选联考 2023] 人员调度

引用别人的话证明 ybw 实力强劲：话说这D1T3真的是人写的吗（雾 虽然口胡出来了但是感觉这玩意放到考试能写出来的保底是个A队水平吧（

ybw /bx

考虑 Hall 定理，如果每棵子树都满足点数 \(\ge\) 子树内的人数，那一定有完美匹配。

把删除换成时间区间，然后线段树分治，这样就只有加入操作了。

考虑如果加入一个人之后没有完美匹配，那就现反悔贪心：找出不满足点数 \(\ge\) 子树内的人数的点中深度最大的，把它子树内中能力最弱的去掉，中间需要用到树剖维护，复杂度 3log，据说可以用全局平衡二叉树做到 2log（虽然我不会）。

口胡还是很舒服的，但有点难写。

记录。

AGC008E Next or Nextnext

神题。

考虑先把图建出来，现在是基环树森林。

先考虑只是环的情况，记环长为 len。手玩可以发现，只有几种情况：

1. \(1 \to 2 \to 3 \to \cdots \to len\)

2. len 为奇数且 len > 1：\(1 \to \frac{len + 1}{2} \to 2 \to \frac{len + 1}{2} + 1 \to 3 \to \frac{len + 1}{2} + 2 \to \cdots \to len \to \frac{len - 1}{2}\)

3. 两个环长度为 len 的环拼起来：\(A_1 \to \to B1 \to A2 \to B2 \to \cdots \to A_s \to B_s\)。

   并且，固定 \(A\)，\(B\) 可以变成一个轮换，有 \(len\) 种。

所以，对于 \(s\) 个长度为 \(len\) 的链，可以枚举情况 3 的个数，计算答案。

再考虑不只是环的情况，手玩可以发现相当于把树上的点插入到环上的空隙中，于是就只能环上的点为链。

每条链的第一个点可以选择最多 2 种插入位置，乘起来即可。

记录。

[AHOI2013] 连通图 DZY Loves Chinese

这题首先有个非常没意思的做法，直接线段树分治即可。这个做法能过前面那个，但前面的强制在线就 G 了。

考虑更高级的做法。我们先随便搜出一棵 DFS 树，对于每条非树边，我们随机一个值 \(x\)，这条边的值就为 \(x\)，并且对于被这条非树边覆盖的边，我们也异或上 \(x\)。

最后图不联通当且仅当能从 \(c\) 条边中找到一个子集，满足边权异或和为 0。

证明：

yuyue /bx

首先，最小割异或和为 0。

考虑由上述方法构造的边权一定满足，对于每个点，定义点权为相邻的所有边权值异或，这个值显然为 0。考虑一个极小的割会将图分成两个集合 A、B，则割即为 A、B之间的连边，也就是 A 集合向外连出去的边。

考虑割的异或和一定等于 A 集合的点权异或和，即为 0。

其次，证明异或和 0 为割。

考虑反证：若不为割，则先把删除的边删掉后，一定能重新找到一棵生成树。现在再把删除的边加回去，则依旧满足上述构造方法的性质。由于原树的非树边权值线性无关，则新树的非树边也应该线性无关。所以与异或和为 0 矛盾。

时间复杂度 \(O(n+q2^c)\) 或 \(O(n+qc\log val_i)\)。其中 \(val_i\) 为随机数的范围。

记录。

CF1548E Gregor and the Two Painters

神题。

连通块计数不好做，考虑对点计数。对于每个连通块，找出其代表点。

这里就有个很神仙的方法，规定代表点为 \(a_i+b_j\) 最小的点，如有多个，按 \((i,j)\) 双关键字排序。

考虑一个点 \((i, j)\) 能走到 \(a_i+b_j\) 更小的点需要满足什么条件。找出 \(la\) 表示 \(i\) 前第一个满足 \(a\) 小于等于它的，\(ra\) 表示 \(i\) 后第一个满足 \(a\) 大于它的，同理得到 \(lb, rb\)。

若一个点能走到 \(a_i+b_j\) 更小的点，当且仅当它能走到第 \(la\) 行或第 \(ra\) 行或第 \(lb\) 列或第 \(rb\) 列。

考虑一个点是否能够到这些位置之间按直线走算即可。因为若走到第 \(la\) 行需要左、右移动，那一定说明左、右 \(b\) 的值更小，所以会被向左、向右的统计到。

于是现在问题的形式就变得非常简单了，我们需要计数 \((i,j)\) 满足：

1. \(a_i+b_j\le x\)；
2. \(a_i+\max\limits_{k=lb_j}^{j}b_k>x\)
3. \(a_i+\max\limits_{k=j}^{rb_j}b_k>x\)
4. \(\max\limits_{k=la_i}^{i}a_k+b_j>x\)
5. \(\max\limits_{k=i}^{ra_i}a_k+b_j>x\)

二维数点即可。

时间复杂度 \(O(n\log n)\)。

记录。

EZEC10D Equalization

考虑先求出差分序列，令 \(d_i=a_{i+1}-a_i\)，\(i\in [1, n - 1]\)，考虑操作的影响：

0. 若 \(l=1\)，\(r=n\)：无意义，举办了。

1. 若 \(l=1\)：\(d_r := d_r - x\)。

2. 若 \(r=n\)：\(d_{l-1} := d_{l-1} + x\)。

3. 否则，\(d_{l-1} := d_{l - 1} + x\) 且 \(d_r := d_r - x\)。

也就是：

1. 操作一：对一个数单独操作，且有两种选择。

2. 操作二：同时对两个数操作，使其和不变。

考虑 \(s\) 个数和为 0 可以全用二操作，操作 \(s-1\) 次使所有数变成 \(0\)。

设 \(f_{mask}\) 表示，选的点集为 \(mask\)，最多能分成的组数。

于是，答案就是 \(n-1-\max\limits_{i = 1} f_i\)。

现在考虑如何算方案数，首先在 DP \(f_{mask}\) 的过程中维护 \(g_{mask}\) 表示方案数。而 \(mark\) 被单独划分成一个不可再分的集合，操作的方案数相当于是在 \(mask\) 个点连 \(mask - 1\) 条边，并要求连通，也是就树，所以答案用 prufer 序列算一下，为 \(|mark|^{|mask|-2}\)。

对于不能用全用操作二的点，记有 \(k\) 个，我们考虑加入一个数 \(a_1-a_n\)。这样就可以保证所有数和为 0。于是就可以沿用上述方法，但需要注意的是操作一有两种选择，也就是说跟新加入的数操作时有两种方案。一个巧妙的做法是把新加入的数看成两个点的连通块。根据经典结论，方案数为 \(2 \times (k+2)^{k-1}\)。

时间复杂度 \(O(3^n)\)。

记录。

CF1704F Colouring Game

考虑两个人显然会优先去消 RB，不妨成为阶段一，然后两个人就分别消 RW 和 BW，不妨称为阶段二。

注意到无论是阶段一还是阶段二，R 和 W 个数的差不变，所以谁的颜色个数多谁就一定获胜。

现在还剩下 R 和 W 个数相同的 case，考虑谁在阶段二先手谁就输，也就是谁一阶段最后一次操作谁赢。

考虑 \(n\) 个格子每个形如 RWRWRW... 的连续段是独立的，于是就可以 SG 函数分别计算。而 SG 函数找规律发现循环节之后就能快速计算了。

时间复杂度 \(O(n)\)。

记录。

CF1553H XOR and Distance

暴力题。。。

先把字典树建出来。

考虑暴力枚举 x，每次相当于是在上一次计算的基础上改变一些二进制，翻转一些二进制位。

翻转第 \(i\) 个二进制位的时间复杂度是 \(O(2^{k-i})\)，从 \(1\) 到 \(2^k-1\) 枚举，需要算 \(2^{k-i}\) 次。

考虑平衡一下，枚举的时候对 \(i\) 在二进制下 reverse 一下，那么第 \(i\) 个二进制位就只会被算 \(2^i\) 次。

时间复杂度 \(O(k2^k)\)。

记录。

CF1730F Almost Sorted

考虑一个排列 \(p\) 满足 \(p_i\le p_j+k(i<j)\) 有什么性质。

从 \(1\) 到 \(n\) 来填数，就需要满足 \([1,p_i-k-1]\) 的数都填完了，所以当前最大值不超过 \(i + k\)。

于是就可以 DP，设 \(f_{i,mask}\) 表示前 \(i\) 个数填完了，\([i+1,i+k]\) 填的状态是 \(mask\) 的最小逆序对数。

时间复杂度 \(O(n 2^k k)\)。

记录。

CF1795G Removal Sequences

赛时看成了第 \(i\) 次操作要删度数为 \(a_i\) 的点，然后 zbl。。。

赛后一看发现是 sb 题。

直接拓扑排序，然后答案就是总对数 - 能到的点对数。

bitset 搞一下就没了。。。

时间复杂度 \(O(\frac{n^2}{w})\)。

记录。

CF1019E Raining season

考虑边分治，这样就考虑左右两个部分的贡献。对左、右两个部分都先求出上凸壳，左右点组合起来就是 \((a_1+a_2,b_1+b_2)\) 的形式，于是用闵可夫斯基和来合并。

最后求答案的时候，把所有闵可夫斯基和上的点合在一起再跑一遍凸包就能得到答案。

注意不要每次得到闵可夫斯基和之后就进行凸包合并，那样复杂度就假了。调了半年。。。

闵可夫斯基和的大小是 \(|A|+|B|\) 的，所以总复杂度就是 \(O(n\log^2 n)\)，瓶颈在于求凸包。

记录。

CF1540D Inverse Inversions

首先先将题目转化一下，计算答案时维护有多少个数比当前询问的数大，若当前有 \(x\) 个数比查询的数大，向右扫，找到 \(b_i\le x\)，则比当前询问的数大的又增加了一个，即 \(x\) 增加 \(1\)。

最后输出 \(n - x\) 即可。

看到数据范围 \(n=10^5\)，时限 5s 想到分块。

我们对操作序列分块，块长为 \(B\)，考虑维护 \(f_{i,j}\) 表示经过第 \(i\) 个块后，本来为 \(j\) 会增加多少。

由于块内总共 \(B\) 个操作，所以 \(f_{i,j}\) 为一个 \(B\) 段的分段函数。

于是考虑使用线段树维护分段函数，每次单点修改时间复杂度 \(O(B)\)。

总时间复杂度是 \(O(m(B + \frac{n}{B}\log B))\)。

\(O(m(B + \frac{n}{B}\log B))<O(m(B + \frac{n}{B}\log n) = O(m\sqrt{n\log n}))\)。

调调块长即可跑得飞快。

记录。

[IOI2000] 邮局 加强版

首先是 wqs 二分，之后就是设 \(f_i\) 表示前 \(i\) 个邮局分配的代价总和。

转移：\(f_i=\min\limits_{j=1}^{i-1} f_j + w(j + 1, i)-k\)。其中 \(w(i,j)\) 算的是 \([i,j]\) 中建一个邮局的最小代价和，显然选择中位数。而 \(k\) 是我们 wqs 二分的值。

由于 \(w\) 函数是满足四边形不等式的，所以 \(f\) 就有决策单调性。考虑用 deque 维护下每个点的转移区间即可。

时间复杂度 \(O(n\log n \log W)\)，其中 \(W\) 是 \(w\) 函数的值域。

记录。

[USACO21DEC] Tickets P

容易把题目转化成对于每个 \(i\) 加代价总和尽量少的边，使得与 \(1\) 和 \(n\) 连通。

相当于是找出到 \(1\) 和 \(n\) 的两条路径，相同部分算同一条。

观察一：\(i\) 到 \(1\) 和 \(n\) 的两条路径，若走到了不同的点，则不会再走回到同一个点，否则肯定可以通过舍弃其中一条路径达到更优解。

观察二：\(i\) 到 \(1\) 和 \(n\) 的两条路径，肯定是前面都是走相同的点，最后再通过一条路径分开，因为最后走到同一条路径了，所以前面走完全相同肯定不劣。

于是，我们先建出反图，可以用线段树优化建图来做。我们求出 \(1\) 和 \(n\) 到每个点的最短路，然后考虑枚举最后走到的相同的路径。这个可以使用 ST 表维护。但是既然都跑最短路了，于是我们可以建一个虚点来维护这个值。

时间复杂度 \(O(n\log^2 n)\)。

记录。

CF1523G Try Booking

首先观察到由于长度 \(x\) 的限制，所以每次选择的区间不超过 \(\frac{n}{x}\)，于是总的选择区间数量是 \(O(n\log n)\) 级别。

于是就可以暴力了，考虑 \(x\) 从大往小做，每次相当于加入一些线段。计算函数 \(calc(l, r)\) 表示 \([l,r]\) 区间当前未被覆盖，求最终覆盖的长度。我们找到在这个区间内编号最小的线段 \(y\)，显然是可以加入的。于是就变成了计算 \(calc(l,l_y-1)\) 和 \(calc(r_y + 1,r)\)。

由于上面所说的性质，所以 \(calc\) 总共会调用 \(O(n\log n)\) 次，每次查询区间内编号最小的线段用树套树维护，所以总复杂度是 \(O(m\log^ 2n+n\log^3 n)\)。但时间跑起来还是很快的。

记录。

AGC010E Rearranging

竟然快速独立做出了 *3887 的 AGC E！！！

首先考虑高桥确定了原序列顺序之后，青木君通过操作能得到什么样的序列。这是个经典问题，类似与 [USACO22JAN] Minimizing Haybales P，考虑由于是交换相邻元素，所以对于两个不互质的元素 \(a_x, a_y(x<y)\)，最后操作的序列一定满足 \(a_x\) 在 \(a_y\) 前面，不难发现这个条件是充要的。

于是只需要建出有向边 \((x,y)\)，跑拓扑排序，中间用 priority_queue 维护。

回到这个题，我们依旧对这样的 \((x,y)\) 建边，不过由于还没有确定顺序，所以我们先建无向边。观察到每个连通块其实是独立的，因为最后每个 DAG 是独立的（相当于最后插进去），所以高桥等价于最小化每个连通块的最大可能拓扑序。

考虑搜出以 \(x\) 为根的 DFS 树（优先遍历值小的），结论是直接按 DFS 树的方式定向就是最优的。

这个做法的正确性在于对每个点连出的所有边内按点值排序。 以 \(x\) 为根的 DFS 树有很多，看到了很多人可能并没有意识到这一点。

下面口胡了个证明：

由于是字典序，所以高桥首先要最小化第一个元素。而若要固定拓扑序的第一个为该连通块的最小值的点 \(x\)，则 DAG 需要满足两个条件：

1. \(x\) 入度为 \(0\)；
2. 其它点入度都不为 \(0\)。

因为首先要保证条件一，所以所有 \(x\) 的出边都是 \(x\) 向下连。

首先考虑没有被非树边覆盖的边。如果有一条向上的边，则由于条件二，一定有子树有向上的边只向它，一直递归下去，一定会到叶子时，然后它的入度为 \(0\) 就非法了。换句话说就是子树内的边数 < 点数，所以肯定非法。

再来考虑被非树边覆盖的边。首先，每个子树是独立的（相当于最后插进去，所以高桥等价于最小化每个子树的最大可能拓扑序。于是，他需要最小化第一个元素，所以要保证非树边深度较大的那个点的入度 > 2，而由于那个点连向儿子的边经过上面证明都是向下的，所以只可以是所有点都向下选才可行。

按 DFS 树定向来建出 DAG，然后再用上面的方法求出答案即可。

时间复杂度 \(O(n^2 \log a)\)，瓶颈在于求 \(\gcd\)。

记录。

[USACO23FEB] Hungry Cow P

赛时开始一眼线段树分治，交了几发都 T 了，就意识到事情不对。后来想了想发现势能分析不能带撤销。。。

后来加了一些不能改变复杂度假了的优化，没过之后就自闭跑路了。。。

赛后听别人说了个楼房重建就明白怎么做了。

首先，我们离线下来把 \(a\) 排序，去重（这样方便一点，不然权值线段树上的空节点得特判），线段树的叶子节点表示的是 \([t_i,t_{i+1})\) 这段区间。为了方便，我们设 \(t_{n+1}=\inf\)。

我们维护当前线段树区间的 \(4\) 个值：

1. 总共匹配了多少个值；
2. 总共向右超出了多少个值；
3. 匹配的答案是多少；
4. 左区间超出部分的答案，若左区间超出部分在右区间依旧超出，那就不管了。

考虑 pushup，分 \(2\) 种情况：

1. 左区间超出部分在右区间依旧超出，则右区间被填满了；
2. 左区间超出部分都可以在右区间插入，我们在右区间做线段树二分，计算出最后一个左区间超出部分的位置。由于需要减掉原始匹配的答案所以具体实现时需要维护 4（在 pushup 的时候记一下）。

写的时候刚睡醒，一个地方 + 和 - 打反了，调了半年。

记录。

[PA2019] Desant

mwr /bx

考虑如何压缩状态。注意到对于每个 \(i\)，前 \(i-1\) 个数形成了若干个连续段，对于每个连续段，我们只关心选了多少个数，而不关心具体选了那些数。

于是就能把状态压得很小，具体而言是 \(O(3^{\frac{n}{3}})\)，相当于是若干和为 \(n\) 的数的乘积。

时间复杂度为 \(O(3^{\frac{n}{3}}n)\)，由于我 SB，所以实际上我写的是 \(O(3^{\frac{n}{3}}n^2)\)（懒得边搜边算了），Luogu 上交需要卡常。

记录。

[NOI2020] 制作菜品

做这道题时根据数据范围的提示较为快速地想出来 \(m=n-1\) 的做法，以及 \(m>n-1\) 的做法。后来又想到了 \(m=n-2\) 就是把数分成两个集合，用 bitset 维护 DP 即可。

再刚准备写时，突然发现我 2020 年打同步赛时写了这题，不过由于当时再 Luogu 提交时没有配 SPJ，爆零了。重交了一下，发现 35 分，把 \(m\ge n-1\) 都过了！然后我仔细看了看我的代码，发现我当时写的贪心能确实在 \(m\ge n-1\) 时是对的，并且方法比我刚刚想的简单很多。之后随便加了个 bitset 维护 DP 就过了。。。

怎么说呢？我当时写这题时，绝对不会从给两个点连边，建出树的角度出发去想题，只会乱写贪心，并随机拿到一定分数。但确实在那年得到了不错的分数，不过仍然无法改变实力不济的事实。

补充下做法：

1. 刚刚想的：

   1. \(m=n-1\)。考虑对两个点建边，生成出一棵树。

      考虑这棵树需要满足什么条件：对于每个点 \(x\)，除了根都要满足子树内的 \(0<(\sum d_i) - (size_x - 1)k<k\) 。把 \(-1\) 去掉，并令 \(val_i=d_i-k\)，则就变成了 \(-k<\sum val_i<0\)。

      另 \(f_i=\sum val_i\)，即子树内的 \(val\) 和。现在我们来构造这棵树，我们将 \(val_i\) 从小到大排序，扫到一个若 \(<0\) 就当叶子，否则就不停地找已经有的点加进去做当前点的儿子。因为之前扫过的 \(-k<f_i<0\)，所以不用担心减过头，并且由于总和，可以保证除了最后一个点（也就是根），都能满足 \(f_i<0\)。

   2. \(m>n-1\)。我们考虑不停地找 \(>k\) 去减掉 \(k\)，直到 \(m=n-1\)，再用上面的做法做。可以根据和容易证明出一定是可以找的到 \(m-(n-1)\) 次 \(>k\) 的数的。

2. 2020 年同步赛的：

   首先说下做法：维护一个 set 存的是 \(d_i\)，每次先取出最小的 \(x\)，然后分两种情况讨论；

   1. 如果 \(x>k\) 减去 \(k\)。
   2. 否则，在 set 中找到任意的 \(\ge k-x\) 的数（直接找最大的即可），并减掉 \(k-x\)。

   证明：不难发现其实和上面的做法是等价的。首先情况 1 相当于是上面的 \(m>n-1\)，情况 2 相当于是把点找儿子，变成了儿子找点。

记录。

[省选联考 2020 A 卷] 作业题

首先是枚举 \(\gcd\) 是 \(i\) 的倍数，然后在容斥下，算出恰好 \(gcd=i\) 的答案。

于是现在问题就是算前者，由于是 \(\sum\limits_{i=1}^{n-1}w_i\)。所以，一个暴力的思路是对每条边都跑一遍 Matrix-Tree。具体而言，我想的是，先设每条边权为 1，求出答案 ans，然后对于每条边，设它权值为 2，求出答案 newans。则包含这条边的方案数为 newans - ans。

考虑在这个基础上优化。\(\sum\limits_{i=1}^{n-1}w_i\) 相当于是构造生成树，并从中恰好选择一条边贡献为 \(w_i\)，其它贡献都是 \(1\)，答案是乘积。所以，我们考虑维护一次函数 \(w_ix+1\)，最后答案就是 \(1\) 次项系数。

至于 \(ax+b\) 求逆，分类讨论；

1. \(b=0\)，\(\frac{1}{ax}\equiv \frac{1}{a}x \pmod {x^2}\)，直接对 \(a\) 求逆元；
2. \(b\ne 0\)，\((ax+b)(ax-b)=-b^2\pmod {x^2}\)，所以 \(\frac{1}{ax+b}\equiv \frac{ax-b}{-b^2} \pmod {x^2}\)。

记录。

[Ynoi2009] rprmq1

首先先猫树分治。按第一维，把询问分成两部分，一部分是猫树上一个节点的前缀询问，另一部分是猫树一个节点的后缀询问。

由于猫树同层节点两两不交，所以我们对每层的猫树节点做扫描线，逐个处理猫树节点上的询问。

我们建出线段树维护列的情况。讨论地将矩形操作变成 \(l_1\) 时刻对 \([l_2, r_2]\) 列加 \(x\)、\(r_1+1\) 时刻对 \([l_2, r_2]\) 列减 \(x\)。

首先我们先考虑前缀询问，我们相当于是查询一段从猫树节点左端点开始的一个时间段的区间历史最大值。这个东西相当于是实现 \(3\) 个操作：

1. 区间加；

2. 将当前值最为历史最大值；

3. 区间查询历史最大值。

操作 2 用 tag 维护下即可。

至于后缀询问，我们做完一个节点的前缀询问后，再倒过来扫，把操作撤销，然后询问。

最后还得再把撤销的操作加回去，所以有个看起来很恐怖的 \(3\) 倍常数。

时间复杂度 \(O(m \log^n n + q\log n)\)，Ynoi 不卡常是真好。

记录。

[HNOI2013] 切糕 RC02D 开门大吉

把多个值选一个转化成最小割断掉一条边。然后考虑限制就直接在对应的值加边，直接这样做就是对的，只要细节都考虑到，就不需要加什么反向边。

记录 1。

记录 2。

[Ynoi2004] rpmtdq

考虑找出支配点对。首先，我们点分治一下。由于问的是最小，在同一子树内的一定只会更劣，不会更优，所以不用管。我们先点分治求出所有点到根的距离 \(dis\)。

将距离按原数组下标排序，从左往右扫，假设当前扫到为 \(x\)。同时，我们维护一个栈表示 \(dis\) 的后缀最小值，支配点对有 \(2\) 种构成方式：

1. 如果当前的栈顶元素 \(dis\) 大于当前栈顶 \(dis\)，则 \(x\) 和栈顶为一个支配点对，因为对于 \(x\) 右侧的点来说跟 \(x\) 一定比跟栈顶优。
2. 弹完之后，如果栈非空，我们再把栈顶和 \(x\) 组成一个支配点对。因为 \(x\) 和非栈顶的其它元素可以劣于栈顶和非栈顶元素组成的点对。

实际上我想的是按 \(dis\) 从小往大排序，每次的新点之后跟坐标第一个比它小的、第一个比它大的组成支配点对，理由跟上面的方式 2 一致。

但这个想法需要用 set，常数太大，无法通过（至少我没能卡过去）。

由于点分治每次要排序，并且支配点对数是 \(O(n\log n)\)，所以总复杂度 \(O(n\log^2 n + q\log n)\)。

记录。

[CTSC2018] 暴力写挂

md，开始看错题了，\(dist(x,y)=dep_x+dep_y-\color{red}2\)\(dep_{lca(x,y)}\)。

首先考虑先边分治一下，现在就考虑边 \((a,b)\) 对应的 \(a\) 部分与 \(b\) 部分的贡献。首先考虑 \(dep_x+dep_y-(dep_{lca(x,y)}+dep'_{lca'(x,y)})=dis_{(x,y)}+dep_{lca(x,y)}-dep'_{lca'(x, y)}\)。

其中 \(dis_{(x,y)}\) 是好算的，然后考虑根节点 \(1\) 肯定在 \(a\) 或 \(b\) 中的一个部分，不妨假设在 \(a\) 部分。于是，\(dep_{lca(x,y)}\) 就可以在 \(a\) 部分直接 \(lca(x, b)\) 算出答案。

然后考虑算 \(dep'_{lca'(x, y)}\)。做法是把边分治的点在第二棵树上建出虚树，再树形 DP 一下即可，维护最大值和次大值。

记录。

CF804E The same permutation

首先考虑到每交换一次，逆序对的奇偶性就会改变，所以有解的一个必要条件是 \(\frac{n(n-1)}{2}\equiv 0 \pmod 4\)，也就是 \(n\equiv 0,1\pmod 4\)。

考虑暴搜出 \(4\) 和 \(5\) 的答案，一个简单的想法是对 \(n\) 个数分块，每个块为 \(4\) 个数或 \(5\) 个数，然后做完块间的操作，使得操作完后每个块的数的集合不变，并且逆序对数依旧是偶数。

通过暴搜发现，可以找到这样的块间构造方案，并且无论块长是 \(4\) 还是 \(5\)，只要逆序对数为偶数，都可以构造出来。

记录。

[BJOI2018] 染色

首先原题的数据巨水……

首先如果有解，这个图肯定得是二分图。然后，如果在这个图中可以找到两个环去掉公共部分剩下的大小都 \(\ge 2\) 就 NO。

因为考虑两个剩余部分都可以这么构造，前面公共部分最后是 AB，一边 AC、CA，这样就限制了不能 A；另一边 BC、CB，这样就限制了不能 B，于是就 NO 了。

考虑如何判断这个东西。首先，如果环的个数 \(\ge 3\) 就无解。证明：首先考虑前两个环，为了不被判成 NO，首先设公共部分为路径 \((a, b)\)。

那么就只要一种情况. 其中一个环 A 点集为 \((a,b)\cap {x}\)，另一个环 B 点集为 \((a,b) \cap {y}\)。容易注意到，\(|(a,b)|\ge 3\) 且第三个环要与 A、B 不无解一定是 \((a,b)\cap {z}\) 之外。容易发现矛盾：环 \({a, z, b}\) 与 \((a,b)\cap {x}\)。

于是就好办了，我们先搜出一棵 DFS 树，然后把返祖边全部拿出来，判断两条返祖边的情况。

好办？个锤子。。。有一车情况。我跟 std 拍挂了 10+ 组才终于正确梳理出了所有情况。具体有点复杂）

别人的做法似乎能证出更强的结论：有解当且仅当是二分图，并且每个连通块是一个环或仅有两个三度点且有两条路径长度为 \(2\)。

不是很懂……

记录。

CF830D Singer House

很神仙的 DP。考虑 \(f_{i,j}\) 表示深度为 \(i\) 的子树内有 \(j\) 条路径的方案数。因为每次一个点只能将两条路径合并为一条，所以由于的 \(j\le n\)，然后就做完了，转移很简单。

时间复杂度 \(O(k^3)\)。

记录。

[PA2013] Raper

做法 1

入门模拟费用流ing，图片来自 神仙command_block的高质量好文：模拟费用流小记，图画得非常好，这里就直接用了）））

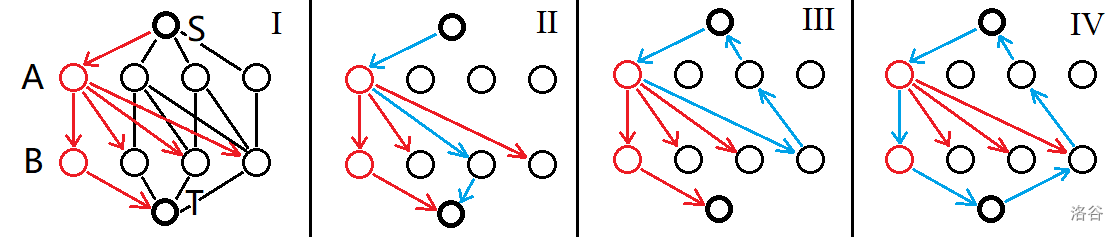
首先，考虑建出费用流模型：

接着，我们 wqs 二分处理 \(k\) 的限制。注意到图 IV 是不可能存在的，因为首先汇点到源点的路径为正，所以这个环的权证总和大于源点到汇点的那条路径，所以劣于图 II。

之后，考虑模拟出反悔边，用一个堆维护。

需要注意的是，模拟费用流维护的是最小费用流，不必保证最大流。

时间复杂度 \(O(n\log n\log a)\)。

记录。

做法 2

非常强悍。

考虑直接上 EK，我们用括号序列来表示出选边的操作，我们考虑増广了 \((S, i)\) 和 \((j,T)\) 两条边，分两种情况讨论：

1. \(i\le j\)，相当于流这条边，括号 ...(...)...；
2. \(i > j\)，相当于反悔操作，括号 ...)...(...。意义是在 \(j\) 前面找到一个点与 \(j\) 匹配，并在 \(i\) 后面找到一个点与 \(i\) 匹配。而能匹配当且仅当括号合法，而括号是否合法取决于是否对于每个位置，左侧的左括号数 \(-\) 左侧右括号数都 \(\ge 0\)。

于是我们用线段树维护整个过程，我们对线段树的每个节点分情况讨论一下即可。

时间复杂度 \(O(n\log n)\)，另外这个做法可以求出对于 \(k=1,2,\cdots,n\) 的所有答案。

[NOI 2019] 序列

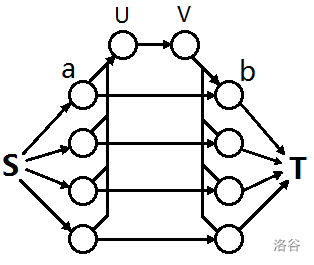
首先，考虑先建出费用流模型：

接着，如图 2，如果 \((U,V)\) 这条边有流量剩余，则我们肯定是直接流，因为这样显然最优，当然主要当如果左部分当前最大和右部分当前最大的编号相同，则可以作为图 1 的流来统计。这样就可以省去分析从图 2 到图 1 的反悔，即图 3 的过程。

然后，我们需要增加同编号边的数量。有 3 种情况：

1. 如图 1，直接流 \((a,b)\)；
2. 如图 4，左侧点反悔，并找出右侧最大点；
3. 如图 5，右侧点反悔，并找出左侧最大点。

注意到我们做 2，3 的过程中可能出现图 3 的情况，需要统计下。

于是我们每次在 3 种情况中找到最优的就可以了。

并更新下就可以了，代码有点难写。其实主要是我写烦了，我写的会去维护左右直接的匹配关系，但实际上只需要维护左右点是否有匹配就可以了。中间图 1 可以根据左右同时有匹配的个数来算。

时间复杂度 \(O(n\log n)\)。宁愿用两个 priority_queue，也不要用 set。

记录。

[USACO22FEB] Redistributing Gifts G

别人问我的题，结果写了半年才过。。。

我的做法挺怪的。首先考虑暴力，先枚举子集，然后 DP 出方案数。具体就是 \(f_{i,mask}\) 表示前 \(i\) 个位置选的数集合为 \(mask\)，值为方案数。这东西显然没前途，考虑这个东西如何一起做，我们发现，这个东西的本质就是找到一个子集，并要求位置集合等于选的数的集合。

然后我就 naive 了，我直接 DP，另 \(f_{i,j,mask}\) 为前 \(i\) 个数中，选的数的个数为 \(j\)，选的数的集合与选的数的集合的并集为 \(mask\) 的方案数，最后要求 \(j = |mask|\)，还好我跟别人讲完之后自己就去写了。看起来很对，实际上忽视了个问题，不同奶牛可能选到相同的数。而且其实我这个 DP 算的就是 \(mask\) 集合里取 \(mask\) 集合的数的方案数。

考虑容斥，计算状态为 \(i\) 的方案数是，我们钦定一个子集 \(j\) 表示选的数的集合不包含 \(j\)，容斥系数为 \((-1)^{|i\backslash j|}\)。直接算是 \(O(3^n n)\)，考虑优化一下，我们预处理出 \(popcount\)，然后先枚举 \(j\)，再枚举 \(i\)，这样就可以递推计算答案做到 \(O(3^n)\)。

代码非常好写。

记录。

CF1503D Flip the Cards

这个题感觉不应该只有 *2600 啊。

首先考虑如果有一张牌正反面都 \(\le n\) 就无解了。因为有一张牌正反面都 \(\le n\)，就一定有牌正反面 \(>n\)，这两张牌无论怎么放都会冲突。

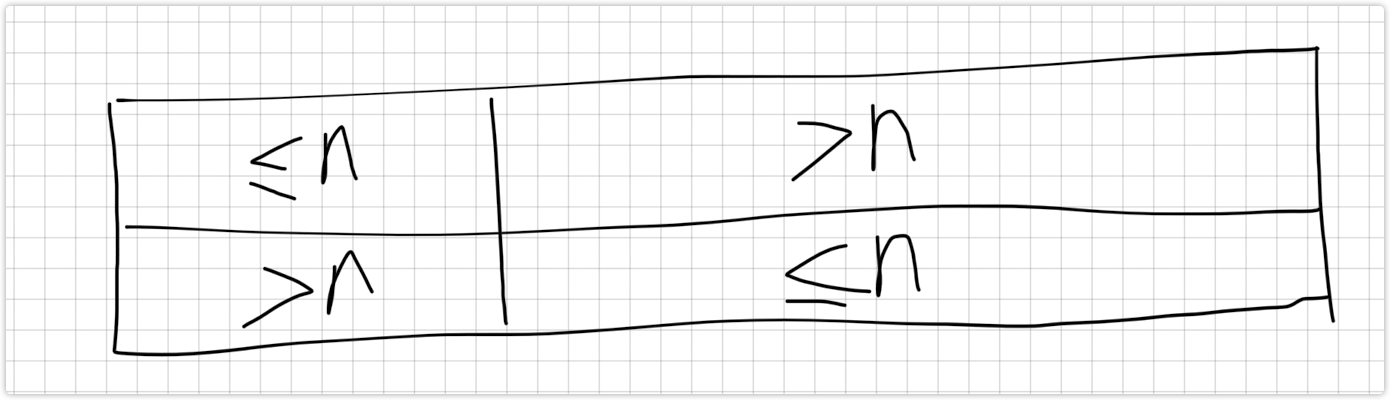
于是现在所以牌就是一面 \(\le n\)，一面 \(>n\)，我们分析一下最终局面，一定形如这样：

第一行的一段前缀 \(\le n\)，后缀 \(>n\)；第二行的对应的那段前缀 \(> n\)，对应的后缀 \(\le n\)。

我们把 \(> n\) 的数映射到 \(\le n\) 上，就变成我们定义 \(f_i\) 表示一面为 \(i\) 的另一面对应的数。

然后就合法方案就等价于将 \(f\) 分成两个互补的下降子序列，注意到还带权，直接 DP 并用 DS 维护可以做到 \(O(n\log n)\)，现在我们考虑如何 \(O(n)\)。

首先，我们发现一个数可能会有两种方案，需要满足它 \(<\) 前缀最小值，因为前面的两个子序列结尾一定有一个是前缀最小值。推广一下结论，如果前缀最小值 \(>\) 后缀最大值，则前面对后面没有影响。将这样的段分开，注意到最终每段方案数不会超过 2。

时间复杂度 \(O(n)\)。

记录。

[NOI2016] 循环之美

LHF 会 6 种做法，我会 0 种。

数论太菜了。

首先，为了算分数个数，我们转化为算最简分数 \(\frac{x}{y}\) 个数，即要求 \(x\perp y\)。

其次，我们考虑如果表示纯循环小数。不妨设其为 \(a=0.c_1c_2\cdots c_p\)。

所以，\(k^p a=\sum\limits_{i=1}^{p}c_ik^{p-i}+a\)，得到 \(a=\frac{\sum\limits_{i=1}^{p}c_ik^{p-i}}{k^p-1}\)。

那么我们 \(\frac{x}{y}\) 合法，当且仅当其能变换成 \(\frac{\sum\limits_{i=1}^{p}c_ik^{p-i}}{k^p-1}\) 的形式，又由于 \(x\perp y\)，所以等价于 \(\exists p,y|k^p-1\)，于是转化成 \(\exists p,k^p\equiv 1 \pmod y\)，从而推出 \((k,y)=1\)。

于是，我们就推出了答案的式子 \(\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}[i\perp j][j\perp k]\)。

然后推式子。

\[\begin{aligned} &\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}[i\perp j][j\perp k]\\ =&\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\sum_{d|(i,j)}\mu(d)[j\perp k]\\ =&\sum_{d}\mu(d)\lfloor\frac{n}{d}\rfloor\sum\limits_{j=1}^{\lfloor\frac{n}{d}\rfloor}[jd\perp k]\\ =&\sum_{d}\mu(d)\lfloor\frac{n}{d}\rfloor[d\perp k]\sum\limits_{j=1}^{\lfloor\frac{n}{d}\rfloor}[j\perp k]\\ \end{aligned} \]

考虑令 \(g(x)=\sum\limits_{i=1}^{x} [i\perp k]\) 是很好算的，\(g(x)=g(x\bmod k)+\lfloor\frac{x}{k}\rfloor \varphi(k)\)，可以 \(O(k\log k)-O(1)\) 求出。

然后整数分块，令 \(f(n)=\sum\limits_{i=1}^{n} \mu(i) [i\perp k]\)。

考虑如何快速计算 \(f\):

\[\begin{aligned} f(n,k)&=\sum\limits_{i=1}^{n} \mu(i) [i\perp k]\\ &=\sum\limits_{i=1}^{n} \mu(i) \sum_{j|(i,k)} \mu(j)\\ &=\sum_{i|k} \mu(i) \sum\limits_{j=1}^{\lfloor\frac{n}{i}\rfloor} \mu(ij)\\ &=\sum_{i|k} \mu(i) \sum\limits_{j=1}^{\lfloor\frac{n}{i}\rfloor} \mu(i)\mu(j) [i\perp j]\\ &=\sum_{i|k} \mu(i)^2 f(\lfloor\frac{n}{i}\rfloor,i)\\ \end{aligned} \]

于是，原式化为：

\[\sum_{l,r}(f(r,k)-f(l-1,k))\lfloor\frac{n}{d}\rfloor g(\lfloor\frac{m}{d}\rfloor) \]

时间复杂度 \(O(n^{\frac{2}{3}}+k\log k+σ(k)\sqrt{n})\)。

记录。

CF757G Can Bash Save the Day?

大 DS 题，从这题中学习了边分树。上文中有讲到过 CF1019E Raining season 这道题，做法是边分树维护凸包合并，求闵可夫斯基和。

于是我们考虑把边分树根线段树一样，每个点维护左部分的总点数、总路径和，右部分的总点数、总路径和。而若加入一个点则是对 \(\log n\) 个节点修改权值，我们可持久化一个，于是我们就得到了主席边分树！！！

对于修改只会改变一棵主席边分树的值，暴力重建一下即可。

时间复杂度 \(O(n\log n)\)。

记录

CF757F Team Rocket Rises Again

做完 G 之后看到 F 做的人也很多，于是就去做了下。首先先把最短路 DAG 建出来，之后相当于是问你，删除一个点后，有多少点不可到。于是这就变成了 DAG 求支配树问题，就做完了。

时间复杂度 \(O(n\log m)\)。

记录。

[NOI2021] 轻重边

先树剖一下，然后我们发现对于非树链上的边最多只有两条，用 vector 维护一下即可，再维护下树链上的边选的个数。

我们发现，对于操作 1：

1. 整链：我们需要支持区间赋值，区间 vector 清空；
2. 链与链之间：我们需要支持单点 vector 清空，单点修改，单点插入。

对于操作 2：

1. 整链：我们需要支持区间查询；
2. 链与链之间：我们需要支持单点查询 vector。

LCA 处会有些细节有点烦，我则直接开摆，直接重新插入一遍。

记录。

CF1749F Distance to the Path

令 \(t\) 为 \(x,y\) 的 LCA。我们考虑转化修改，我们考虑把修改转化成在 \((a,b,k)\) 表示在 \(a\) 的子树内距离 \(a\) 为 \(b\) 的点加 \(k\)。于是首先，我们会有 \((t,0,k)\)，我们往下推，则会有 \((son_t,0,k)\)，\((son_t,1,k)\)，一直往下，直到 \((t,d,k)\)，\((t,d-1,k)\)，而对于路径 \((x,y)\) 上的其它点 \(z\)，则可以推得为 \((z,d,k)\)。

用 BIT 维护一下即可。

记录。

CF1503E 2-Coloring

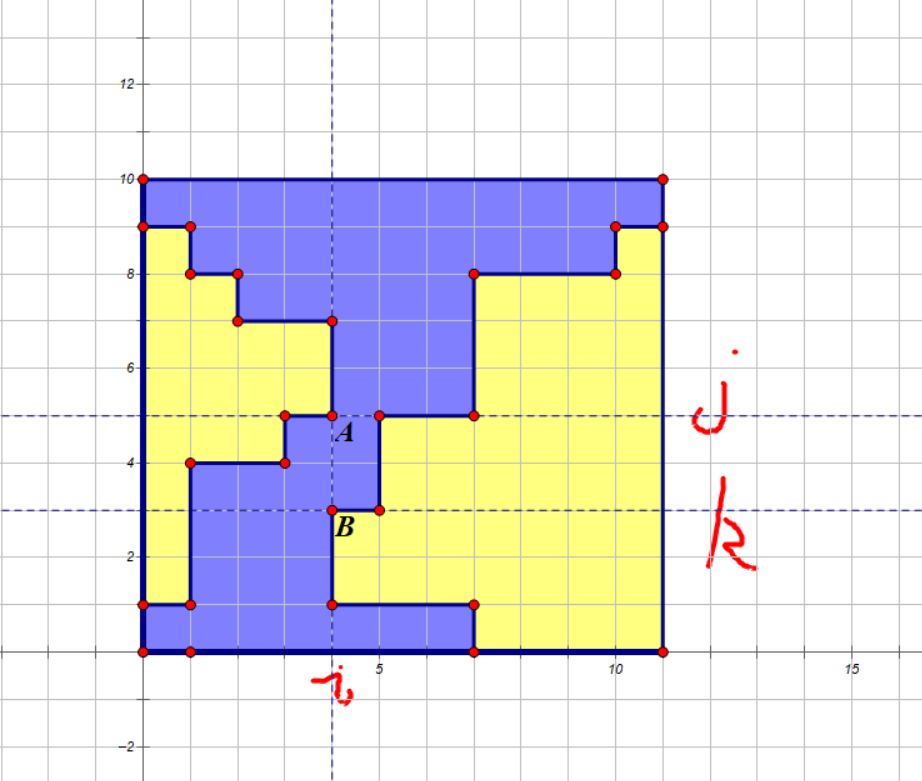
观察下合法图形的性质，我们发现总共只有 3 种情况：

1. 蓝色连通、黄色不连通；
2. 蓝色不连通、黄色连通；
3. 蓝色、黄色都连通。

首先，1、2 是对称的，相当于把 \(n,m\) 交换一下。我们考虑 1 的情况。注意到这时，黄色一定是两个单峰状。

答案就是

\[\sum_{i=1}^{m}\sum_{j=1}^{n-1}\sum_{k=j+1}^{n}f(j-1,i)f(n-j,i-1)f(k-1,m-i-1)f(k,m-i) \]

其中 \(f(x,y)\) 表示的是 \(x\) 个 \([0,y]\) 之间从小到大排序过的数的方案数，也就是 \(\binom{x+y}{x}\)。

并且注意到这个式子可以统计到情况 3（\(k=j+1\) 的情况）。

记录。

gym102411D Double Palindrome

lyx /bx

对于能分成两个回文串的串进行计数，我们不妨先对划分方式进行计数，然后就不会了。

主要根据 Cry-For-theMoon's blog 的方法，并补充了正确的证明。

首先，我们称一个串是本原的当且仅当其有唯一方式拆分成两个回文串（允许为空）。

以前写的。

有一个非常强大的结论：若一个串 $s$ 有至少两种拆分方式，则其一定是由一个本原串复制若干遍而得到。

看完 crying 的证明决定自己证一遍然后发现是假的/kk。

考虑其中的两种拆分方式为分别在 \(p,q(p<q)\) 处划分，注意到 \(prefix_p\) 和 \(prefix_q\) 都是回文串，所以 \(prefix_p\) 是 \(prefix_q\) 的 border，于是 \(prefix_q\) 有长度为 \(len=q-p\) 的周期 \(prefix_{len}\)。令 \(r = q\bmod len\)，则 \(q\) 的前 \(r\) 个字符组成的字符串与最后 \(r\) 个字符组成的字符串一样，又因为 \(q\) 回文，所以 \(prefix_r\) 回文，同理能得到 \(suffix_{len-r}\) 回文。

同理，得到的是 \(suffix_{(|S|-q)\bmod len}\) 回文。

而事实上右侧剩下字符的数量可能不为 \(len - r\)，而又无法说明 \(len | |s|\)，并且确实存在 \(len\nmid |s|\) 的情况，例如 s=aaaaa，p=1，q=3。

于是就假了。

正确的证明还不太会，先鸽了。

UPD：正确的证明方式 yuyue/bx

考虑其中的两种拆分方式为分别在 \(p,q(p<q)\) 处划分，注意到 \(prefix_p\) 和 \(prefix_q\) 都是回文串，所以 \(prefix_p\) 是 \(prefix_q\) 的 border，于是 \(prefix_q\) 有长度为 \(len=q-p\) 的周期 \(prefix_{len}\)。并称 \(s_{len}=s[p+1,q]\)。

令 \(r = q\bmod len\)，则 \(q\) 的前 \(r\) 个字符组成的字符串与最后 \(r\) 个字符组成的字符串一样，又因为 \(q\) 回文，所以 \(prefix_r\) 回文，并称这个字符串为 \(s_l\)，同理能得到 \(suffix_{(|S|-q)\bmod len}\) 回文，并称这个字符串为 \(s_r\)。

容易证明，\(s_{len}-s_l\) 和 \(s_{len}-s_r\) 也都是回文字符串，证明方法同上。

于是，我们就证出了 \(s\) 有两种拆分方式，形式跟原问题相同，于是递归下去，边界是 \(|s_l|+|s_r|=|s_{len}|\) 或者 \(|s_l|=|s_r|=0\)。不难发现肯定可以达到。

此外，做这个题还有一个重要结论：所有本原字符串重复若干遍构成的串互不相同。

好证吗？感觉更难证啊/kk。

先留个坑。

现在重新写一遍（因为杂题选讲要讲这个题）：

定义一个串是本原的当且仅当其有唯一方式拆分成两个回文串（允许为空）。

结论 \(1\)：若一个串 \(s\) 有至少两种拆分方式，则其一定是由一个本原串复制若干遍而得到。

证明：考虑其中的两种拆分方式为分别在 \(p,q(p<q)\) 处划分，注意到 \(prefix_p\) 和 \(prefix_q\) 都是回文串，所以 \(prefix_p\) 是 \(prefix_q\) 的 border，于是 \(prefix_q\) 有长度为 \(len=q-p\) 的周期 \(prefix_{len}\)。并称 \(s_{len}=s[p+1,q]\)。

令 \(r = q\bmod len\)，则 \(q\) 的前 \(r\) 个字符组成的字符串与最后 \(r\) 个字符组成的字符串一样，又因为 \(q\) 回文，所以 \(prefix_r\) 回文，并称这个字符串为 \(s_l\)，同理能得到 \(suffix_{(|S|-q)\bmod len}\) 回文，并称这个字符串为 \(s_r\)。

容易证明，\(s_{len}-s_l\) 和 \(s_{len}-s_r\) 也都是回文字符串，证明方法同上。

于是，我们就证出了 \(s\) 有两种拆分方式，形式跟原问题相同，于是递归下去，边界是 \(|s_l|+|s_r|=|s_{len}|\) 或者 \(|s_l|=|s_r|=0\)，则说明 \(s_{[p+1,q]}\) 是 \(s\) 的真循环节。

结论 \(2\)：所有本原串复制若干遍得到的串不同。

证明：若本原字符串 \(s_1\) 复制 \(a\) 次与本原字符串 \(s_2\) 复制 \(b(a\ne b)\) 次相同，则说明 \(\gcd(|s_1|,|s_2|)\) 为 \(s_1\) 和 \(s_2\) 真循环节，令其为 \(s_3\)。

令 \(s_1\) 的唯一划分在 \(p\) 处。

若 \(p\) 不在 \(s_1\) 的正中间，则可以在 \(|s_1|-p\) 划分，所以 \(s_1\) 不为本原字符串。

否则 \(p\) 在 \(s_1\) 的正中间。则可以说明 \(s_3\) 回文，所以 \(s_1\) 有超过 \(1\) 种划分方式。

有了这个结论就随便做了。记 \(f_i\) 为长度为 \(i\) 的有两种拆分方式的串的个数，然后再去计算 \(g_i\) 表示长度为 \(i\) 的本原串的个数，按照结论减去不合法的串即可。

时间复杂度 \(O(n\log n)\)。

记录。