【大联盟】20221203 T2 guess
guess
题目描述
给定 ,有一个机器存储了一个 \([1,n]\) 中的整数 \(k\)。你可以不断地询问这个机器一个正整数 \(x\)。若 \(x\ne k\) ,机器会返回给你 \(k\) 与 \(x\) 的大小关系,你的目标是猜出这个隐藏的数 。
其中,如果机器给出 \(>\),则会带来 \(a\) 的代价,给出 \(<\) 则会带来 \(b\) 的代价,你希望最坏的情况下你消耗的代价尽可能小,那么该如何进行询问呢?请输出这个最小的代价。
\(1\le n\le 10^{12}\)
题解
现场得分:50/100(脑子坏了)
观察到这道题跟扔鸡蛋很像,于是首先考虑暴力 DP,\(f_i\) 表示询问区间长度为 \(i\) 的最小代价。
\(f_i=\min\limits_{j=1}^{i} \{\max{f_{j-1},f{n-j}}\}\)
显然有决策单调性,于是暴力右移决策点,时间复杂度 \(O(n)\),期望得分 \(30\)。
现场做法:
观察到 \(f_i\) 有很多连续段,考虑每次先对当前状态 \(f_x\) 二分找出决策点 \(j\)(\(f_{j-1}<f_{x-j}\)),然后计算出 \(f_i\) 的值,再二分出当前决策点可求出答案的右端点 \(r\),把 \([l, r]\) 作为整体压进 vector 里面即可。
代码
#include <bits/stdc++.h>
#define SZ(x) (int) x.size() - 1
#define all(x) x.begin(), x.end()
#define ms(x, y) memset(x, y, sizeof x)
#define F(i, x, y) for (int i = (x); i <= (y); i++)
#define DF(i, x, y) for (int i = (x); i >= (y); i--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); }
const long double eps = 1e-8;
long double a, b;
ll n;
vector <pair <ll, long double> > v;
int query(ll x) {
return lower_bound(all(v), make_pair(x, (long double) 0)) - v.begin();
}
long double calc(ll x, ll y) {
long double ans = 1e18;
int t1 = query(y - 1), t2 = query(x - y);
if (y) chkmin(ans, max(v[t1].second + (y > 1) * a, v[t2].second + (y < x) * b));
t1 = query(y), t2 = query(x - y - 1);
if (y < x) chkmin(ans, max(v[t1].second + (y + 1 > 1) * a, v[t2].second + (y + 1 < x) * b));
return ans;
}
signed main() {
freopen("guess.in", "r", stdin);
freopen("guess.out", "w", stdout);
cin >> n >> a >> b;
ll x = 2;
v.emplace_back(0ll, 0.0);
v.emplace_back(1ll, 0.0);
while (x <= n) {
int l1 = 1, r1 = v.size();
while (l1 + 1 < r1) {
int mid = (l1 + r1) >> 1;
if (v[mid].second + a - (v[query(x - v[mid - 1].first)].second + b) < eps) l1 = mid;
else r1 = mid;
}
long double ans = calc(x, v[l1].first);
v.emplace_back(x, ans);
ll l2 = x, r2 = n + 1;
while (l2 + 1 < r2) {
ll mid = (l2 + r2) >> 1;
if (mid - v[l1].first <= x && fabs(calc(mid, v[l1].first) - ans) < eps) l2 = mid;
else r2 = mid;
}
v.emplace_back(l2, ans);
x = l2 + 1;
} cout << fixed << setprecision(10) << v.back().second;
return 0;
}
可以通过 \(1\le a, b\le 10^3\) 的数据,期望得分 \(50\)。
但是考虑不满足 \(1\le a, b\le 10^3\) 的情况,一种极端情况是 \(a=1, b = 10^9\),这样显然 \(f_i=i \le [1,10^9]\),然后就 TLE 了。
正解:
理解一:
考虑 \(n\) 个点对于的不同询问状态,类似于一个 \(n\) 个点的二叉树:
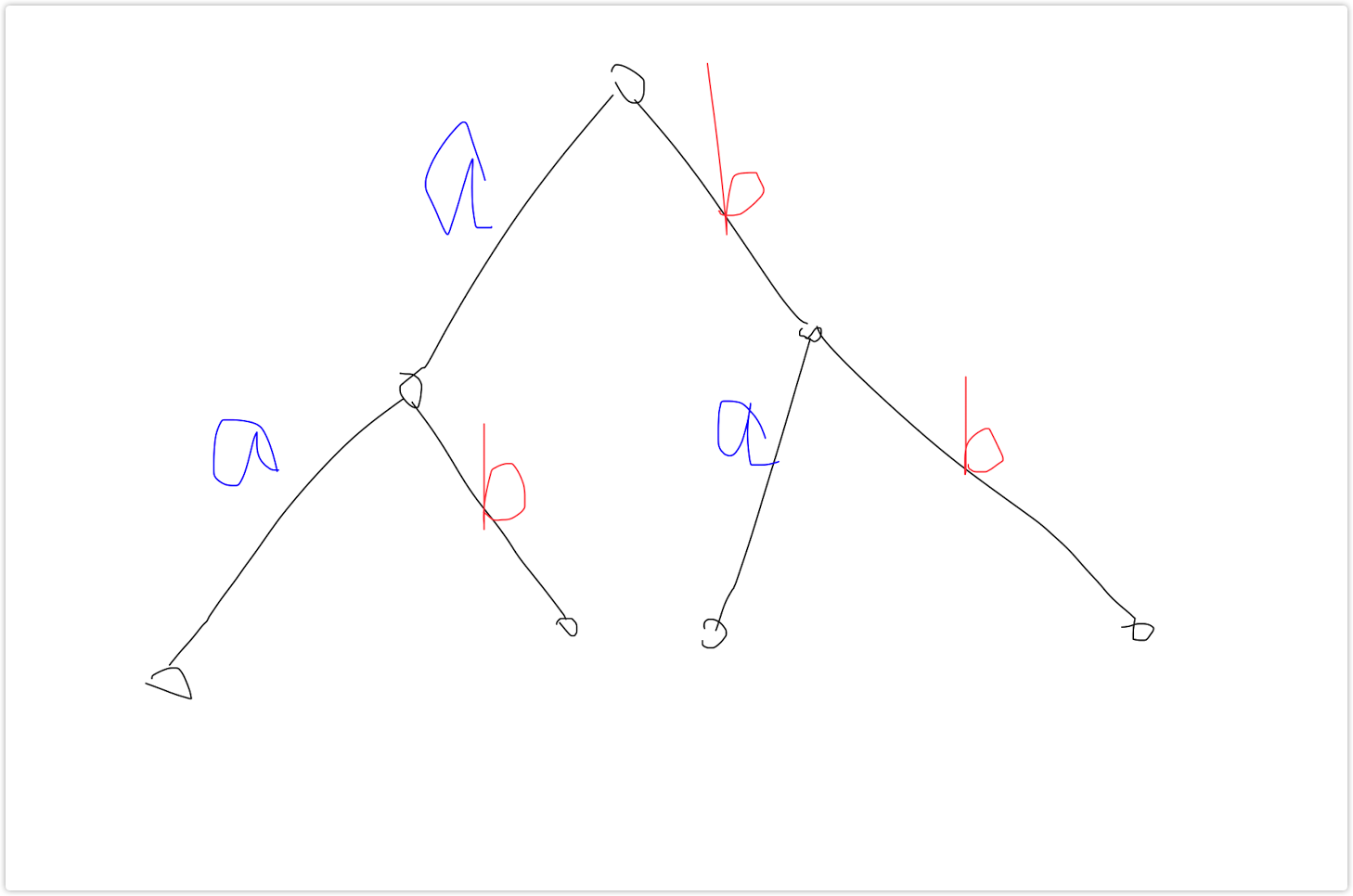
每个点的代价是其对应路径的权值总分。
考虑二分答案,判断是否答案 \(\le mid\),即为求 \(ax+by\le mid\) 的整数解对应路径的个数。
对于路径个数即为 \(f_{x, y}=C(x+y,x)\)。
理解二:
考虑 \(f_{x,y}\) 表示 \(a\) 使用次数恰好为 \(x\),\(b\) 使用次数恰好为 \(y\) 能确定多少个数。考虑最后一次询问室 \(a\) 还是 \(b\),于是 \(f_{x,y}=f_{x-1,y}+f_{x,y-1}, f_{x,0}=f_{0,x}=1\)。
考虑二分答案,判断是否答案 \(\le mid\),即为求 \(ax+by\le mid\) 的整数解对于 \(f_{x,y}\) 的和。
考虑 \(f_{x,0}\) 和 \(f_{0,y}\) 对 \(f_{x,y}\) 的贡献,即为 \(C(x + y, x)\)。
至此,题目转化成判断 \(\sum_\limits {ax+by\le mid} C(x + y, x) \le mid\)。
考虑答案不会超过 \(\log_2(n) \times \max{a, b}\),于是 \(\min(x, y) \le \log_2(n)\)。
不妨假设 \(a>b\),那么即为 \(x \le \log_2(n)\),暴力枚举 \(x\),考虑计算出 \(y_{\max}\),则对应贡献为:\(\sum_\limits{y=1}^{y_{\max}} C(x + y, x) = C(x + y + 1, x + 1)\)。
代码
#include <bits/stdc++.h>
#define SZ(x) (int) x.size() - 1
#define all(x) x.begin(), x.end()
#define ms(x, y) memset(x, y, sizeof x)
#define F(i, x, y) for (int i = (x); i <= (y); i++)
#define DF(i, x, y) for (int i = (x); i >= (y); i--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
template <typename T> void chkmax(T &x, T y) {x = max(x, y); }
template <typename T> void chkmin(T &x, T y) {x = min(x, y); }
const int N = 55;
const double eps = 1e-8;
ll n;
int k;
double a, b;
bool check(double x) {
ll s = 0;
F(i, 0, k) {
if (x - a * i < 0) break;
ll t = (x - a * i + eps) / b;
int x = i + t + 1, y = min(t, (ll) i + 1);
ll z = 1;
F(j, 1, y) {
z = z * (x - j + 1) / j;
if (z + s >= n) return true;
} s += z;
} return false;
}
signed main() {
freopen("guess.in", "r", stdin);
freopen("guess.out", "w", stdout);
cin >> n >> a >> b;
if (a < b) swap(a, b);
k = log2(n) + 1;
double l = 0, r = k * max(a, b);
F(i, 1, 100) {
double mid = (l + r) / 2.0;
if (check(mid)) r = mid;
else l = mid;
}
cout << fixed << setprecision(10) << r;
return 0;
}


