题解 P3651 【展翅翱翔之时 (はばたきのとき)】

题目意思：

有 \(n\) 个点，第 \(i\) 点有一条出边 \(i\to a_i\)。更改点 \(x\) 的出边代价为 \(c_x\)，要求用最小的代价将所有点连成一个环。

我们先把原图建出来，考虑这张图一定是若干个树连环。

每一个弱连通块一定是类似于这样：

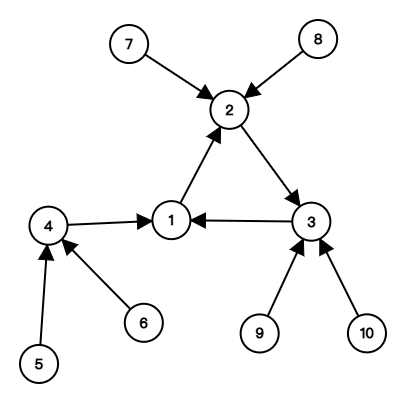
即：

我们的任务则是找到最长的一条链。

对于一条链，每个节点的入度最多为 \(1\)​​，所以，对于树上的点，为了最大化答案，我们选择保留入边中边权最大的一条。

对于环上的点，我们也可以这样做，因为至少去掉的那些边一定不可能被选进最优解中去。

经过这样的处理，还剩下这样的东西：

这个环是处理的重中之重。

对于环上的一个点，环上与它相邻的点的两条边以及子树的一条边至少会断一条边（没有子树，可以看成有一条边权为 \(0\) 的边）。

我们还发现，我们必须断至少一条环上的边，必须至少保留一条来自子树连向环的边，否则就不为链了。

最后还有一个小细节需要特判一下：

如果这个图本身强联通，答案应为 \(0\)。

代码（目前的最优解）：

#include<bits/stdc++.h>
#define log(a) cerr<<"\033[32m[DEBUG] "<<#a<<'='<<(a)<<" @ line "<<__LINE__<<"\033[0m"<<endl
#define LL long long
#define SZ(x) ((int)x.size()-1)
#define ms(a,b) memset(a,b,sizeof a)
#define F(i,a,b) for(int i=(a);i<=(b);++i)
#define DF(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
inline int read(){char ch=getchar(); int w=1,c=0;
    for(;!isdigit(ch);ch=getchar()) if (ch=='-') w=-1;
    for(;isdigit(ch);ch=getchar()) c=(c<<1)+(c<<3)+(ch^48);
    return w*c;
}
const int N=1e5+10;
int a[N],b[N],h[N],f[N],l[N];
LL ans;
bool vis[N];
queue<int>q;
int main(){
    int n=read();
    F(i,1,n){
        a[i]=read(),b[i]=read();
        h[a[i]]++;
    }
    F(i,1,n)
        if(!h[i])q.push(i);
    if(q.empty()){
        int s=0;
        for(int i=1;!vis[i];i=a[i])s++,vis[i]=true;
        if(s==n){
            puts("0");
            return 0;
        }
    }
    while(q.size()){
        int x=q.front();q.pop();
        if(f[a[x]]){
            ans+=min(f[a[x]],b[x]);
            f[a[x]]=max(f[a[x]],b[x]);
        }else f[a[x]]=b[x];
        if(--h[a[x]]==0)q.push(a[x]);
    }
    F(i,1,n)
        if(h[i]){
            int tot=0;
            for(int j=i;h[a[j]];j=a[j]){
                h[a[j]]=0;
                ans+=f[a[j]];
                l[++tot]=f[a[j]]-b[j];
            }
            sort(l+1,l+tot+1);
            ans-=l[tot];
            DF(i,tot-1,1)
                if(l[i]>0)ans-=l[i];
        }
    cout<<ans;
    return 0;
}