题解 P6100 【[USACO19FEB]Painting the Barn G】

这道题首先考虑把求面积转化成求满足条件的格点数量，接着考虑怎么做。因为这两个矩形没有交，所以一个点最多只会被覆盖一次。于是最终答案中 \(K\) 层涂料的只可能是初始下 \(K-1\) 层涂料（被涂一层）和 \(K\) 层涂料（没有被涂）。

于是就考虑转化，涂了 \(K-1\) 层的格子标记为 \(1\)，即涂了这个格子能是答案加 \(1\)；涂了 \(K\) 层涂料的格子标记为 \(-1\)，因为涂了这个格子会使答案减少 \(1\)，最终的答案就是双子矩阵最大和，这可以看作是双子序列最大和的延续和拓展。

考虑两个子矩阵的相对位置：

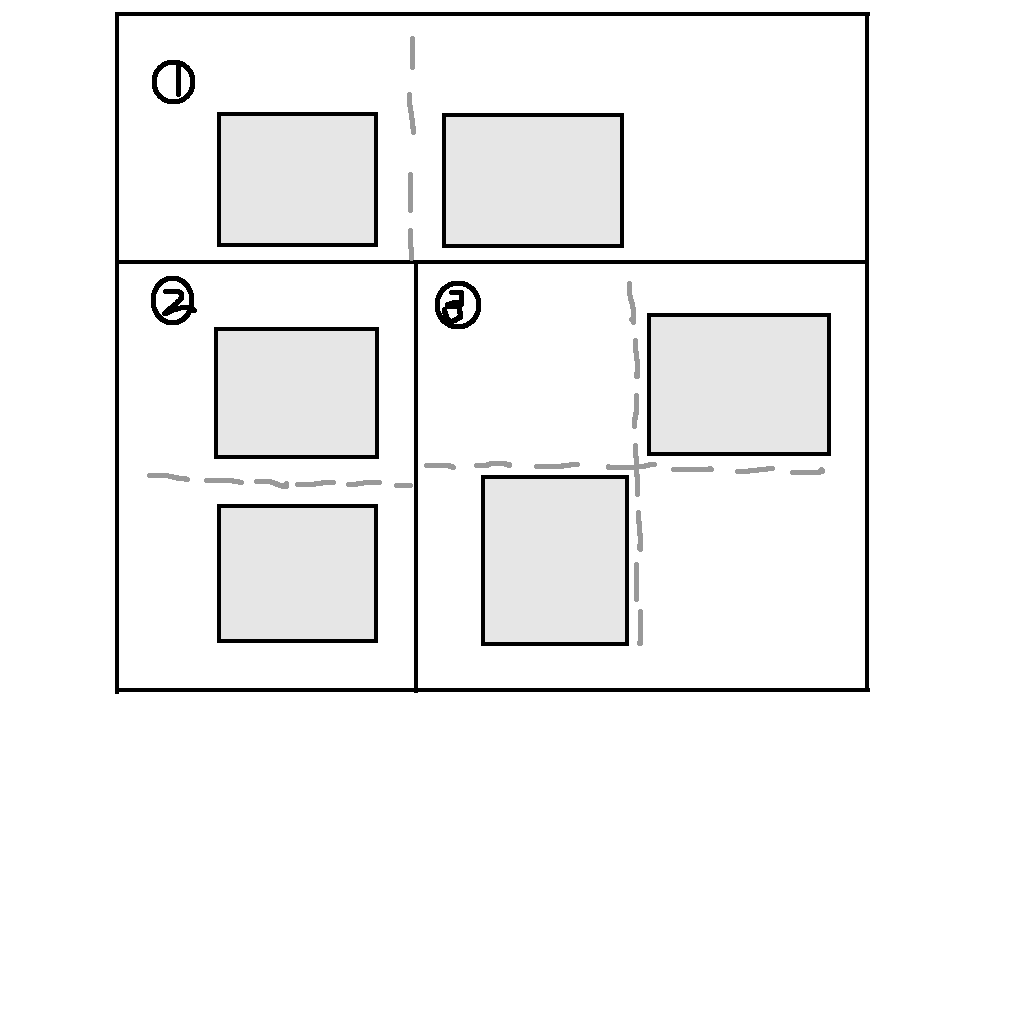
第三种可以看作是前两种情况的公共部分。

对于前两种情况，我们可以枚举分割线，求出答案。对于分割线的两边，我们可以 \(4\) 个方向都做 \(dp\)，枚举两个边界去求。最后记得前缀 \(\max\) 一下，因为不一定一定要贴着分割线，判断没有即对 \(0\) 取 \(\max\) 即可。

具体看代码（自认为实现非常清晰）：

#include<bits/stdc++.h>
#define log(a) cerr<<"\033[32m[DEBUG] "<<#a<<'='<<(a)<<" @ line "<<__LINE__<<"\033[0m"<<endl
#define LL long long
#define SZ(x) ((int)x.size()-1)
#define ms(a,b) memset(a,b,sizeof a)
#define F(i,a,b) for(int i=(a);i<=(b);++i)
#define DF(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
inline int read(){char ch=getchar(); int w=1,c=0;
	for(;!isdigit(ch);ch=getchar()) if (ch=='-') w=-1;
	for(;isdigit(ch);ch=getchar()) c=(c<<1)+(c<<3)+(ch^48);
	return w*c;
}
const int N=210;
int f[N][N],lf[N][N][N],rf[N][N][N],uf[N][N][N],df[N][N][N],s1[N][N],s2[N][N],lmaxn[N],rmaxn[N],umaxn[N],dmaxn[N],ans,s;
//l表示left（左），r表示right（右），u表示up（上），d表示down（下）
//f[i][j]表示这个格子的值（使用前缀和快速处理）
//l/r/u/df[i][j][k]表示上界为i，下界为j，处理到k
//l/r/u/dmaxn[i]表示前缀/后缀求max到i
//s1[i][j]表示f[1][j]~f[i][j]的和
//s2[i][j]表示f[i][1]~f[i][j]的和
signed main(){
	int n=read(),k=read();
	F(i,1,n){
		int kx=read()+1,ky=read()+1,tx=read(),ty=read();//转换为割点数：kx,ky加上1，让每个点表示它左下角的格子
		f[kx][ky]++;f[kx][ty+1]--;f[tx+1][ky]--;f[tx+1][ty+1]++;//差分
	}
	F(i,1,200)
		F(j,1,200){
			f[i][j]+=f[i-1][j]+f[i][j-1]-f[i-1][j-1];//前缀和即为值
			int t=0;//如果不是k或k-1就为0
			if(f[i][j]==k)t=-1,s++;//处理矩阵元素值
			if(f[i][j]+1==k)t=1;//处理矩阵元素值
			s1[i][j]=s1[i-1][j]+t;//求前缀和
			s2[i][j]=s2[i][j-1]+t;//求前缀和
		}
	F(i,1,200)
		F(j,i,200){
			F(k,1,200){
				lf[i][j][k]=max(lf[i][j][k-1],0)+s1[j][k]-s1[i-1][k];//dp（跟不跟左边相连）
				lmaxn[k]=max(lmaxn[k],lf[i][j][k]);//求这一列为右边界，左边的最大值
			}
			DF(k,200,1){
				rf[i][j][k]=max(rf[i][j][k+1],0)+s1[j][k]-s1[i-1][k];//dp（跟不跟右边相连）
				rmaxn[k]=max(rmaxn[k],rf[i][j][k]);//求这一列为左边界，右边的最大值
			}
			F(k,1,200){
				uf[i][j][k]=max(uf[i][j][k-1],0)+s2[k][j]-s2[k][i-1];//dp（跟不跟上边相连）
				umaxn[k]=max(umaxn[k],uf[i][j][k]);//求这一行为下边界，上面的最大值
			}
			DF(k,200,1){
				df[i][j][k]=max(df[i][j][k+1],0)+s2[k][j]-s2[k][i-1];//dp（跟不跟下边相连）
				dmaxn[k]=max(dmaxn[k],df[i][j][k]);//求这一行为上边界，下面的最大值
			}
		}
	F(i,1,200)lmaxn[i]=max(lmaxn[i-1],lmaxn[i]);//前缀max
	DF(i,200,1)rmaxn[i]=max(rmaxn[i+1],rmaxn[i]);//前缀max
	F(i,1,200)umaxn[i]=max(umaxn[i-1],umaxn[i]);//前缀max
	DF(i,200,1)dmaxn[i]=max(dmaxn[i+1],dmaxn[i]);//前缀max
	F(i,1,200)ans=max(ans,max(lmaxn[i]+rmaxn[i+1],umaxn[i]+dmaxn[i+1]));//枚举分界线求值
	cout<<s+ans;//主要加上初始值
	return 0;
}