题解 SP1716 【GSS3 - Can you answer these queries III】
前言
首先说一下题意。就是每次给出 \(x\) 和 \(y\) 两个数，求 \(x\) 到 \(y\) 这个区间的最大子段和。
正文
分析
首先我们看这个数据范围，我们显然是要用线段树来做这道题。
我们考虑如何 pushup。
pushup 的操作
区间最大子段和
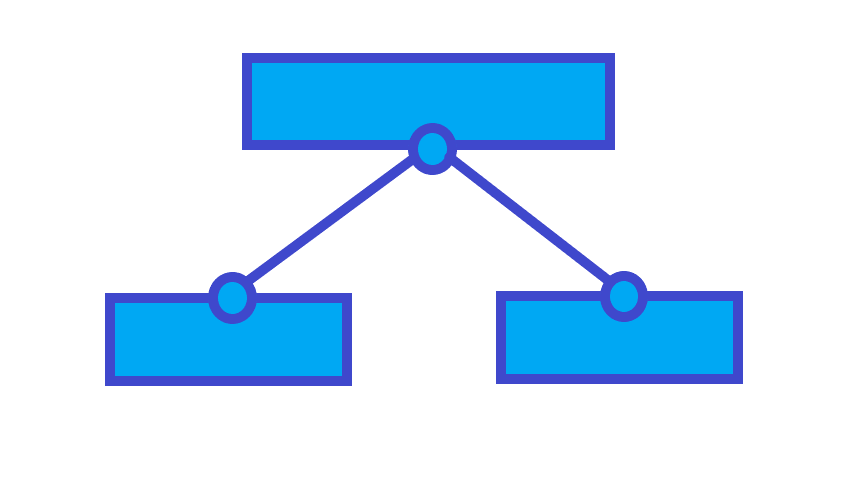
我们考虑一个区间的最大子段。
我们分 \(3\) 种情况讨论：
1. 有可能是左边部分的最大子段和
答案就是左边部分的最大子段和。
2. 也有可能右边部分的最大子段和
答案就是右边部分的最大子段和。
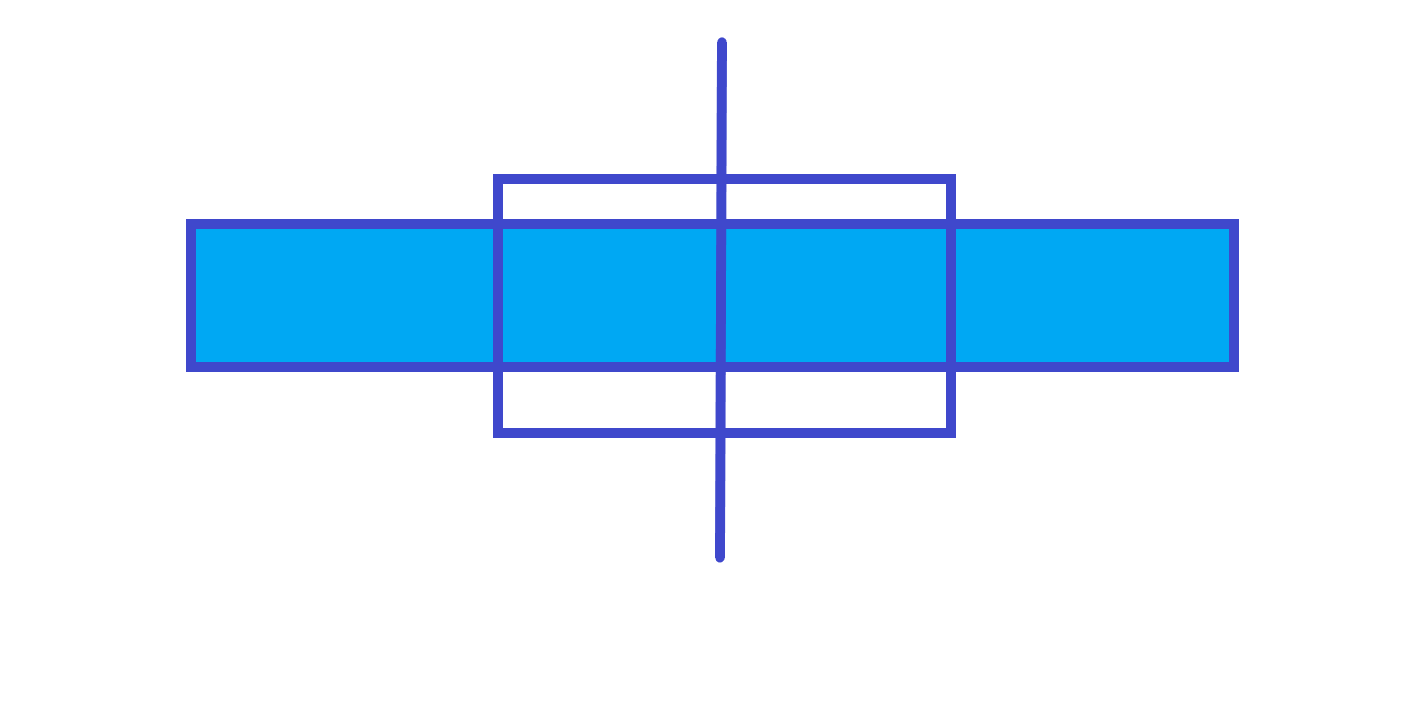
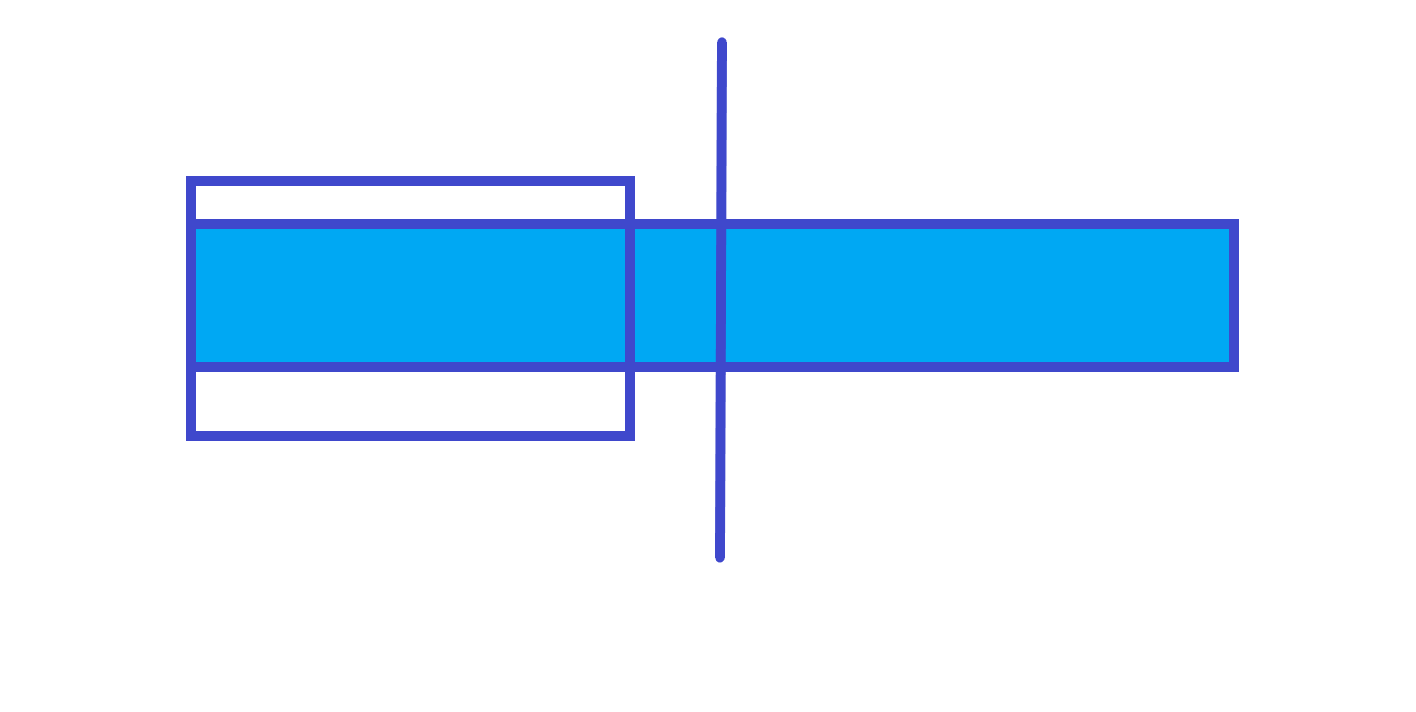
3. 最大最大和有可能跨越了中间
答案就是左边部分右端点往左的最大子段和 \(+\) 左端点往右的最大子段和。
发现
所以，我们需要对于所有节点，还要维护它们以左端点往右的最大子段和、右端点往左的最大子段和。
我们再考虑如何维护一个区间以左端点往右的最大子段和、右端点往左的最大子段和。
以左端点往右的最大子段和
我们先考虑以左端点往右的最大子段和。
我们分 \(2\) 种情况讨论：
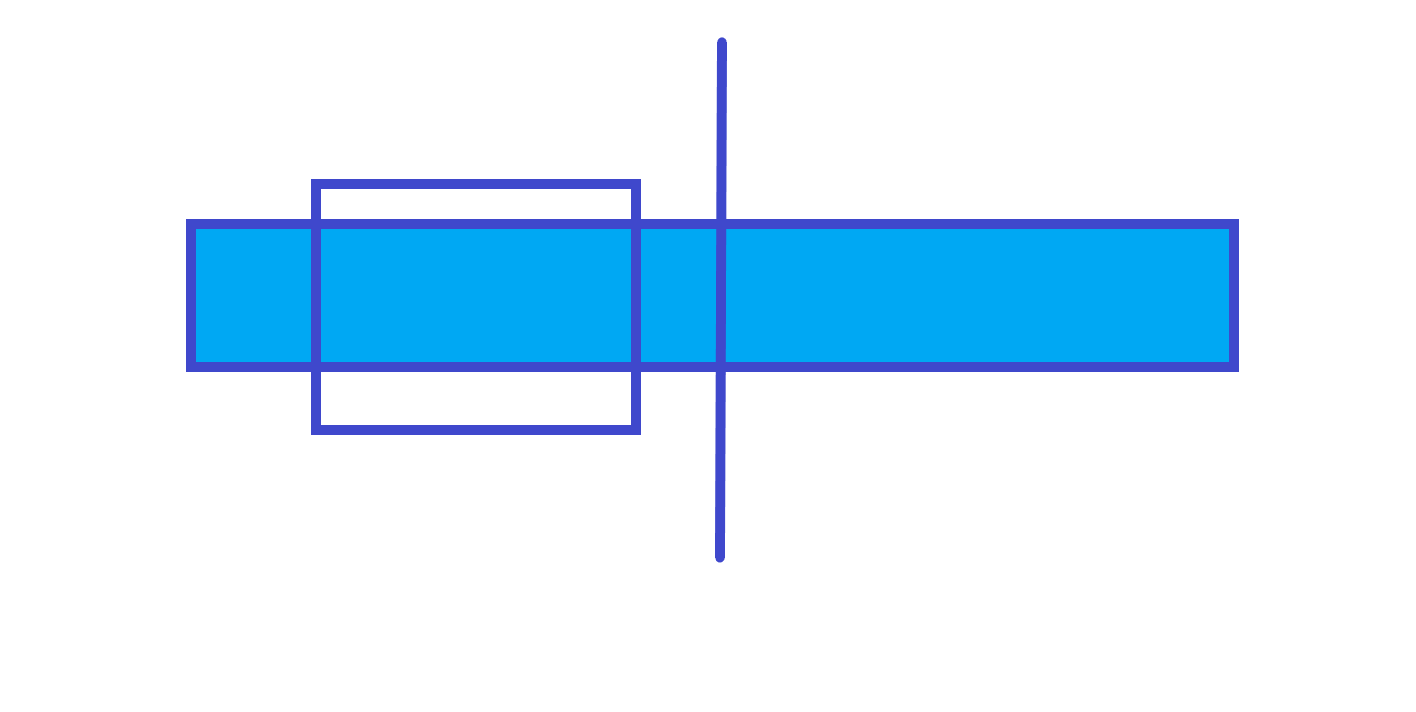
1. 不跨越中间
答案就是左部分的以左端点往右的最大子段和。
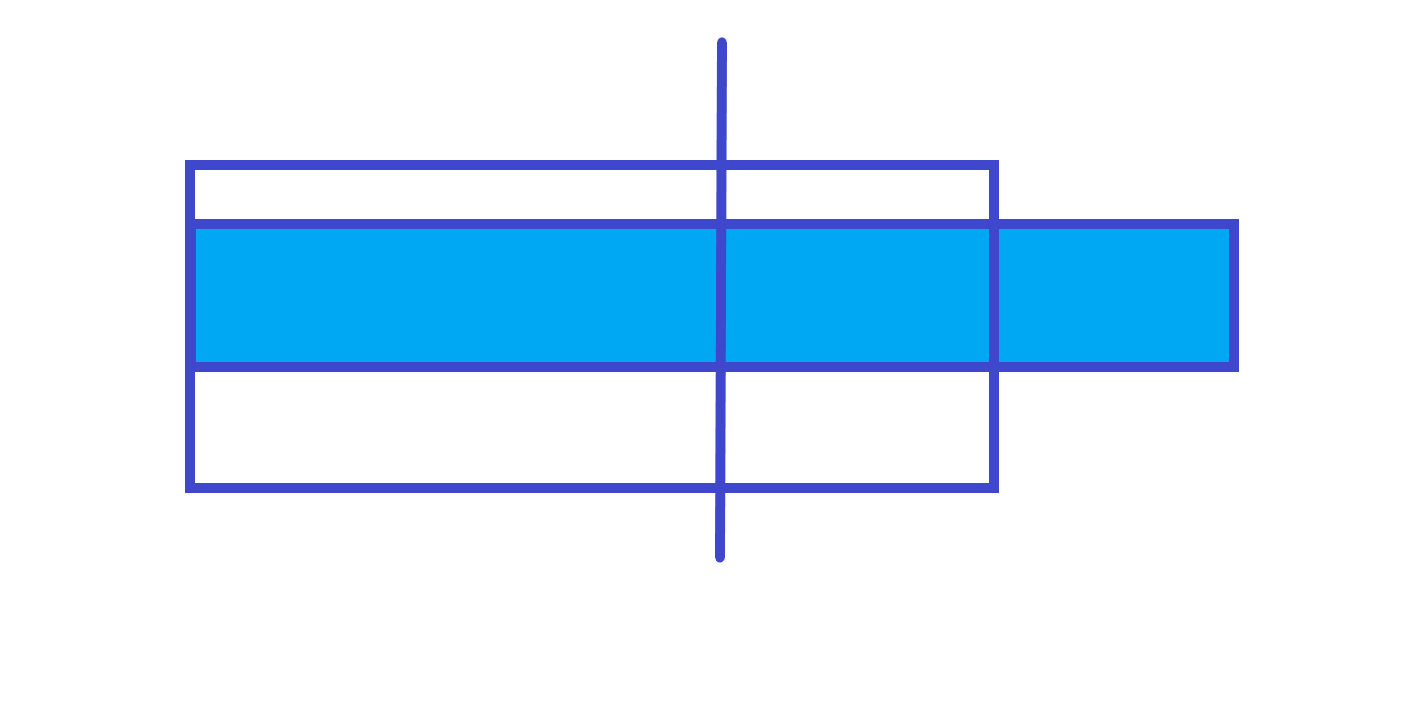
2. 跨越中间
答案就是左部分的和 \(+\) 右部分以左端点往右的最大子段和。
以右端点往左的最大子段和
我们先考虑以右端点往左的最大子段和。
我们分 \(2\) 种情况讨论：
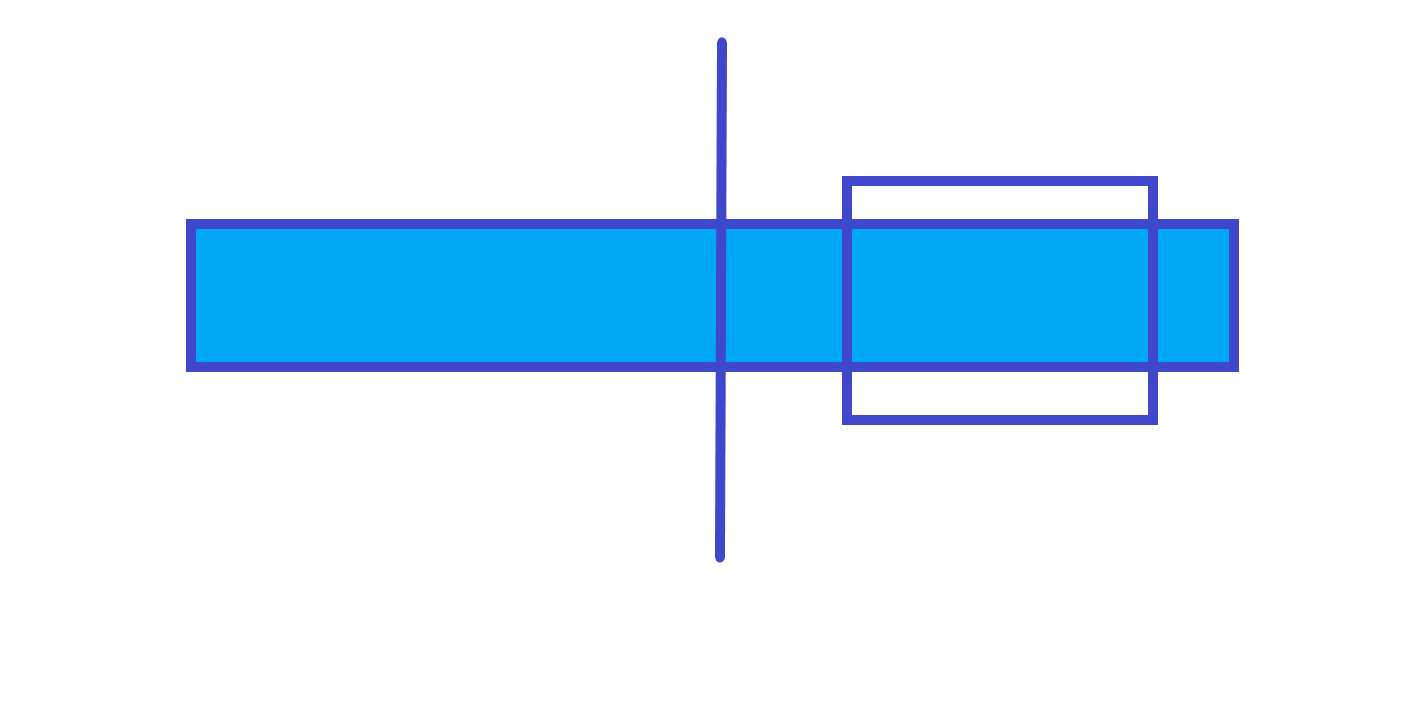
1. 不跨越中间
答案就是右部分的以左端点往右的最大子段和。
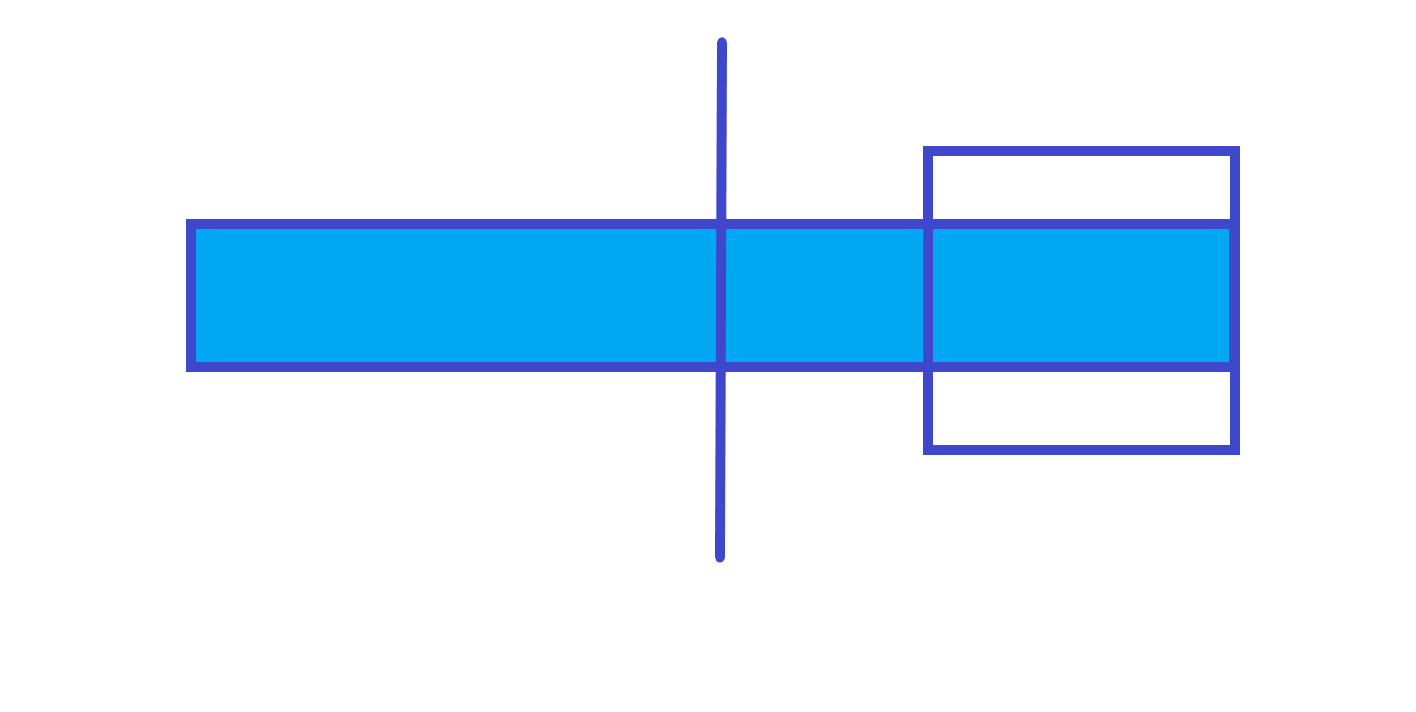
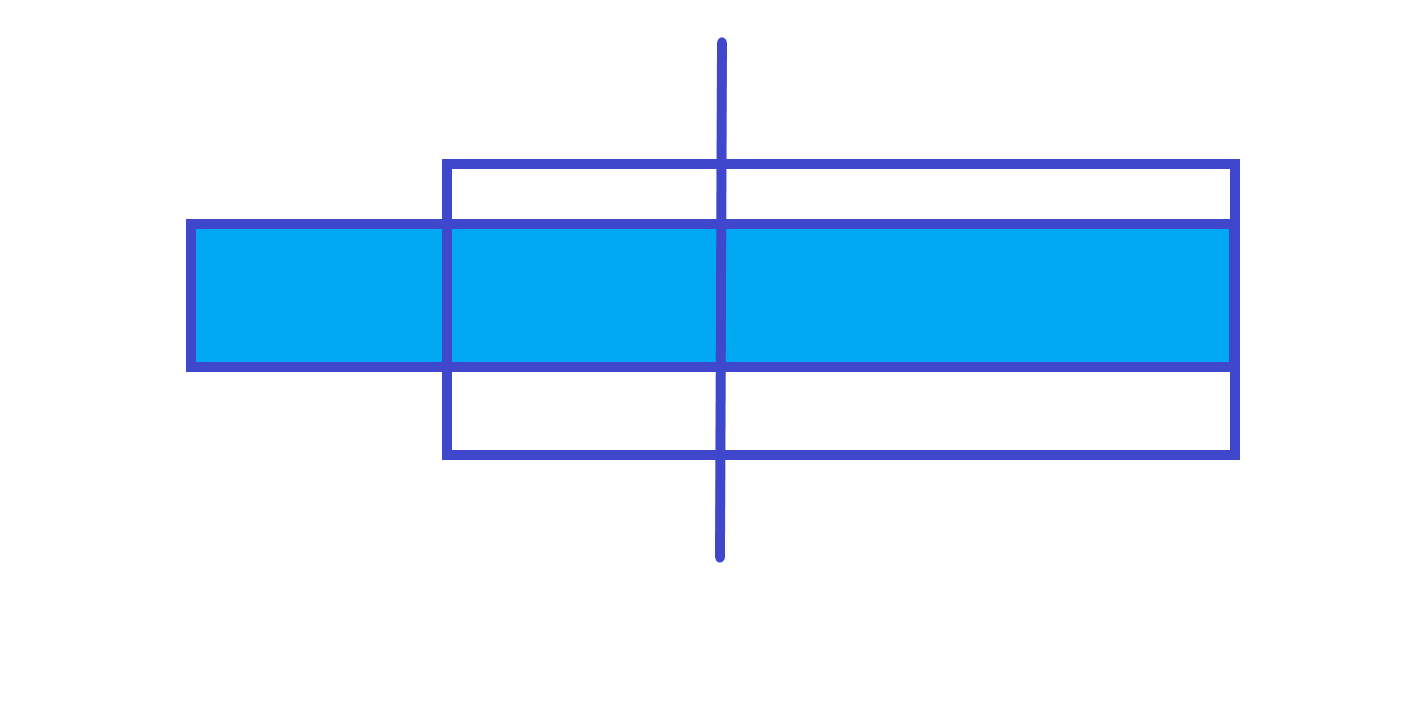
2. 跨越中间
答案就是右部分的和 \(+\) 左部分以右端点往左的最大子段和。
发现
我们发现我们还需要维护区间和，这个问题很简单，不再讲解了。
所以我们现在总共要维护 \(4\) 个东西。
分别是：
\(lans\)、\(rans\)、\(ans\)、\(sum\)。
边界情况——即整个区间是一个点
我们可以发现：
\(lans\)、\(rans\)、\(ans\)、\(sum\) 都为这个点的值。
代码
Tree pushup(Tree L,Tree R){
Tree z;
z.sum=L.sum+R.sum;//和
z.l=max(L.l,L.sum+R.l);//2种情况
z.r=max(R.r,R.sum+L.r);//2种情况
z.ans=max(max(L.ans,R.ans),L.r+R.l);//3种情况
return z;
}
这里我写了一个带返回值的函数，就是为了下面方便啦。
查询
上文已经讲解了最大子段和的 \(3\) 中情况，已经知道最大子段和跟 \(4\) 个东西有关。
所以我们要定义一个返回值为 \(Tree\) 的函数。
那么现在，关键就在于合并区间，那么现在之前的pushup就可以被调用了。
Tree query(int x,int y,int num,int l,int r){
if(x<=l&&r<=y)return t[num];
int mid=(l+r)>>1;
if(y<=mid)return query(x,y,ls,l,mid);//右区间和查询区间没有交，答案当然在左区间
if(mid<x)return query(x,y,rs,mid+1,r);//左区间和查询区间没有交，答案当然在右区间
return pushup(query(x,mid,ls,l,mid),query(mid+1,y,rs,mid+1,r));//是不是很简洁？
}
代码
我们已经把这道题的重点都搞清楚了，接下来就可以放代码了，至于单点修改不会的请自行去学习。
#include <bits/stdc++.h>
#define ls num<<1
#define rs num<<1|1
using namespace std;
template<typename T>inline void read(T &FF){
T RR=1;FF=0;char CH=getchar();
for(;!isdigit(CH);CH=getchar())if(CH=='-')RR=-1;
for(;isdigit(CH);CH=getchar())FF=(FF<<1)+(FF<<3)+(CH^48);
FF*=RR;
}
template<typename T>void write(T x){
if(x<0)putchar('-'),x*=-1;
if(x>9)write(x/10);
putchar(x%10+48);
}
template<typename T>void writen(T x){
write(x);
puts("");
}
const int MAXN=5e4+10;
struct Tree{
int sum,l,r,ans;//维护的4个量
}t[MAXN*4];
int a[MAXN],f,x,y;
Tree pushup(Tree L,Tree R){
Tree z;
z.sum=L.sum+R.sum;//和
z.l=max(L.l,L.sum+R.l);//2种情况
z.r=max(R.r,R.sum+L.r);//2种情况
z.ans=max(max(L.ans,R.ans),L.r+R.l);//3种情况
return z;
}
void build(int l,int r,int num){//建树
if(l==r){
t[num].sum=a[l];
t[num].l=a[l];
t[num].r=a[l];
t[num].ans=a[l];//边界初始化
return;
}
int mid=(l+r)>>1;
build(l,mid,ls);
build(mid+1,r,rs);
t[num]=pushup(t[ls],t[rs]);//pushup
}
void change(int l,int r,int num){//单点修改
if(l==r){
t[num].sum=y;
t[num].l=y;
t[num].r=y;
t[num].ans=y;//边界初始化
return;
}
int mid=(l+r)>>1;
if(x<=mid)change(l,mid,ls);
else change(mid+1,r,rs);
t[num]=pushup(t[ls],t[rs]);
}
Tree query(int x,int y,int num,int l,int r){
if(x<=l&&r<=y)return t[num];
int mid=(l+r)>>1;
if(y<=mid)return query(x,y,ls,l,mid);//右区间和查询区间没有交，答案当然在左区间
if(mid<x)return query(x,y,rs,mid+1,r);//左区间和查询区间没有交，答案当然在右区间
return pushup(query(x,mid,ls,l,mid),query(mid+1,y,rs,mid+1,r));//是不是很简洁？
}
int main(){
int n,T;
read(n);
for(int i=1;i<=n;i++)read(a[i]);
build(1,n,1);
read(T);
while(T--){
read(f);read(x);read(y);
if(f==0)change(1,n,1);
else writen(query(x,y,1,1,n).ans);
}
return 0;
}
