分割田地
前言
这道题目呢,真的很复杂。
考试的时候呢,看到如此小的数据,就写了个搜索,写好之后一测,发现不对了。发现了一种情况。

然后我就 \(fst\) 了,还有 \(5\) 分钟,我终于想到了 \(dp\),这也就是正解。
然后没写完 \(qwq\)。
正文
分析
我们定义:\(f_{i,j,0/1}\) 代表前 \(i\) 列,分割成 \(j\) 份,最后一列 \(2\) 块是否在同一块地。
这就好办了
我们必须考虑两列。因为此列是否跟前一列连,也是很重要的。
然后,我们可以开始分类讨论。
为了方便看,我用了四种颜色来画。分别是红、黄、橙、绿。
这 \(1\) 列 \(2\) 个格子不在一块
我们先考虑最后 \(2\) 块颜色不一样的情况。
前 \(1\) 列 \(2\) 个格子不在一块
情况 \(1\)

\[f_{i,j,0}+=f_{i-1,j-2,0}
\]
情况 \(2\)

\[f_{i,j,0}+=f_{i-1,j-1,0}
\]
情况 \(3\)

\[f_{i,j,0}+=f_{i-1,j-1,0}
\]
注意:情况 \(3\) 和情况 \(2\) 为 \(2\) 种不同的情况,一定不要漏考虑。
情况 \(4\)
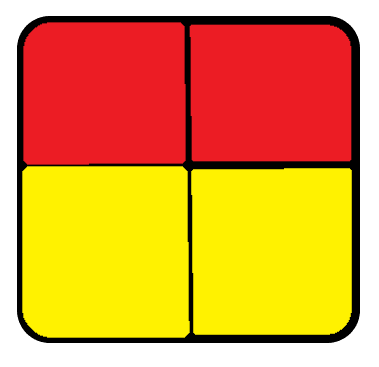
\(f_{i,j,0}+=f_{i-1,j-0,0}\)
前 \(1\) 列 \(2\) 个格子在一块
情况 \(1\)

\[f_{i,j,0}+=f_{i-1,j-2,1}
\]
情况 \(2\)

\[f_{i,j,0}+=f_{i-1,j-1,1}
\]
情况 \(3\)

\[f_{i,j,0}+=f_{i-1,j-1,1}
\]
注意:情况 \(3\) 和情况 \(2\) 为 \(2\) 种不同的情况,一定不要漏考虑。
这 \(1\) 列 \(2\) 个格子在一块
前 \(1\) 列 \(2\) 个格子不在一块
情况 \(1\)

\[f_{i,j,1}+=f_{i-1,j-1,0}
\]
情况 \(2\)

\[f_{i,j,1}+=f_{i-1,j-0,0}
\]
情况 \(3\)

\[f_{i,j,1}+=f_{i-1,j-0,0}
\]
注意:情况 \(3\) 和情况 \(2\) 为 \(2\) 种不同的情况,一定不要漏考虑。
这 \(1\) 列 \(2\) 个格子在一块
情况 \(1\)

\[f_{i,j,1}+=f_{i-1,j-1,1}
\]
情况 \(2\)

\(f_{i,j,1}+=f_{i-1,j-0,1}\)
代码
代码就应该很好写了。
我是写了记忆化搜索,因为非法情况和边界条件很多。
非法
if(i==1){
if(k==1)return j==1;//如果第1列的2个格子颜色相同,只能分割成1分。
return j==2;//如果第1列的2个格子颜色不相同,只能分割成2分。
}
边界
if(j==1)return 1;
你会发现,
状态转移方程
经过上面的推导,状态转移方程也是水到渠成了。
状态转移方程:
if(k==0){
f[i][j][0]+=dfs(i-1,j-2,0);
f[i][j][0]+=dfs(i-1,j-1,0);
f[i][j][0]+=dfs(i-1,j-1,0);
f[i][j][0]+=dfs(i-1,j-0,0);
f[i][j][0]+=dfs(i-1,j-2,1);
f[i][j][0]+=dfs(i-1,j-1,1);
f[i][j][0]+=dfs(i-1,j-1,1);
}else{
f[i][j][1]+=dfs(i-1,j-1,0);
f[i][j][1]+=dfs(i-1,j-0,0);
f[i][j][1]+=dfs(i-1,j-0,0);
f[i][j][1]+=dfs(i-1,j-1,1);
f[i][j][1]+=dfs(i-1,j-0,1);
}
总代码
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
template<typename T>inline void read(T &FF){
T RR=1;FF=0;char CH=getchar();
for(;!isdigit(CH);CH=getchar())if(CH=='-')RR=-1;
for(;isdigit(CH);CH=getchar())FF=(FF<<1)+(FF<<3)+(CH^48);
FF*=RR;
}
template<typename T>void write(T x){
if(x<0)putchar('-'),x*=-1;
if(x>9)write(x/10);
putchar(x%10+48);
}
int n,k,f[1010][2010][2];
bool h[1010][2010][2];
int dfs(int i,int j,int k){
if(i==1){
if(k==1)return j==1;
return j==2;
}
if(j==1)return 1;
if(h[i][j][k])return f[i][j][k];
h[i][j][k]=true;
if(k==0){
f[i][j][0]+=dfs(i-1,j-2,0);
f[i][j][0]+=dfs(i-1,j-1,0);
f[i][j][0]+=dfs(i-1,j-1,0);
f[i][j][0]+=dfs(i-1,j-0,0);
f[i][j][0]+=dfs(i-1,j-2,1);
f[i][j][0]+=dfs(i-1,j-1,1);
f[i][j][0]+=dfs(i-1,j-1,1);
}else{
f[i][j][1]+=dfs(i-1,j-1,0);
f[i][j][1]+=dfs(i-1,j-0,0);
f[i][j][1]+=dfs(i-1,j-0,0);
f[i][j][1]+=dfs(i-1,j-1,1);
f[i][j][1]+=dfs(i-1,j-0,1);
}return f[i][j][k];
}
int main(){
read(n);read(k);
write(dfs(n,k,0)+dfs(n,k,1));
return 0;
}
调错
然后你会发现你连样例都过不了,原来是有一种错误的情况在这里骗吃骗喝。
——\(j=1,k=0\)
这一列 \(2\) 两个格子颜色不同,还分成 \(1\) 份?显然是错的(我在这里死了 \(1 h\))
总代码
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
template<typename T>inline void read(T &FF){
T RR=1;FF=0;char CH=getchar();
for(;!isdigit(CH);CH=getchar())if(CH=='-')RR=-1;
for(;isdigit(CH);CH=getchar())FF=(FF<<1)+(FF<<3)+(CH^48);
FF*=RR;
}
template<typename T>void write(T x){
if(x<0)putchar('-'),x*=-1;
if(x>9)write(x/10);
putchar(x%10+48);
}
int n,k,f[1010][2010][2];
bool h[1010][2010][2];
int dfs(int i,int j,int k){
if(i==1){
if(k==1)return j==1;
return j==2;
}
if(k==0&&j==1)return 0;
if(j==1)return 1;
if(h[i][j][k])return f[i][j][k];
h[i][j][k]=true;
if(k==0){
f[i][j][0]+=dfs(i-1,j-2,0);
f[i][j][0]+=dfs(i-1,j-1,0);
f[i][j][0]+=dfs(i-1,j-1,0);
f[i][j][0]+=dfs(i-1,j-0,0);
f[i][j][0]+=dfs(i-1,j-2,1);
f[i][j][0]+=dfs(i-1,j-1,1);
f[i][j][0]+=dfs(i-1,j-1,1);
}else{
f[i][j][1]+=dfs(i-1,j-1,0);
f[i][j][1]+=dfs(i-1,j-0,0);
f[i][j][1]+=dfs(i-1,j-0,0);
f[i][j][1]+=dfs(i-1,j-1,1);
f[i][j][1]+=dfs(i-1,j-0,1);
}return f[i][j][k];
}
int main(){
read(n);read(k);
write(dfs(n,k,0)+dfs(n,k,1));
return 0;
}
后记
这里作者大概花了 \(3.5hs\) 的时间,整理,画图,写了这道题的代码
已经把我认为的所有都考虑了,如果有遗漏,欢迎找我补充。


