排序算法详解 一
1.插入排序
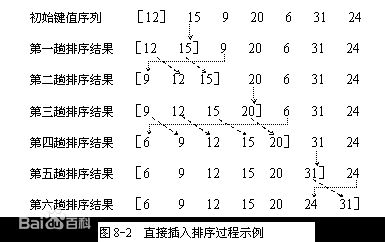
//Description :最差情况下,直接插入排序的最大时间代价为θ(n²),最小时间代价为θ(n),平均时间代价为θ(n²)。
void InserSort(int array[],int n) { for (int i=1;i<n;++i) { for (int j=i;j>0;--j)//以0到i为遍历区间 { if (array[j]<array[j-1]) swap(array,j,j-1); else break;//为>时即可知是有序数组即break } } }
2.冒泡排序

图示是依次从大到小找到各个元素,下面代码依次从小到大找到各个元素
//Description :冒泡排序的最大时间代价,最小时间代价和平均时间代价均为θ(n²)(稳定)。
void BubbleSort(int array[],int n) { for (int i=0;i<n-1;i++)//通过n-1次循环一次将最小值排到最左边 { for (int j=n-1;j>i;--j)//从右边开始遍历 { if(array[j]<array[j-1]) swap(array,j,j-1); } } }
3.选择排序

//Description :选择排序的最大时间代价,最小时间代价和平均时间代价均为θ(n²)。选择排序不依赖于原始数组的输入顺序。(稳定)
void SelectionSort(int array[],int n) { for (int i=0;i<n-1;++i)//外循环,用smallest不断抽取最小值 { int smallest=i; for(int j=i+1;j<n;++j)//内循环找到smallest { if(array[smallest]>array[j]) smallest=j; } swap(array,i,smallest); } }
4.希尔排序(特殊的插入排序)

//Description :增量为2的shell排序的时间代价可以达到θ(n的3/2次方),有的增量可以达到θ(n的7/6次方),很接近θ(n)。
void ShellSort(int array[],int n) { for(int delta=n/2;delta>0;delta/=2) for(int i=0;i<delta;++i) for(int j=i+delta;j<n;j+=delta) for(int k=j;k>0;k-=delta) { if(array[k]<array[k-1]) swap(array,k,k-1); else break; } }


