排序算法详解 二

1.归并算法步骤:

  1>分解:将无序序列不断分裂,直到每个区间都只有一个数据为止(递归实现)

  2>合并:将两个区间合并为有序区间,一直合并到只有一个区间为止(分治思想)

下面代码为归并过程:

//归并过程--将两个有序的数组合并成一个有序数组
void merge(int array[],int left,int middle,int right)
{
    int *tempArray = new int[right-left+1]; 
    int index1=left;
    int index2=middle+1;
    int i=0;
    while(index1<=middle&&index2<=right)
    {
        if (array[index1]<=array[index2])
            tempArray[i++]=array[index1++];
        else
            tempArray[i++]=array[index2++];
    }
    while (index1<=middle)
        tempArray[i++]=array[index1++];
    while (index2<=right)
        tempArray[i++]=array[index2++];
    for(int j=0;j<i;++j)
        array[left+j]=tempArray[j];
    delete[] tempArray;
}

下图为递归和合并有序的过程(时间复杂度为NlogN)

//递归大法好
void MergeSort(int* array,int left,int right)
{
    if(left>=right||array==NULL) return;
    //if(right-left<2) return ;
    int middle=(left+right)/2;
    MergeSort(array,left,middle);
    MergeSort(array,middle+1,right);
    merge(array,left,middle,right);
}

 2.快速排序步骤:

   1>构造轴点::选择一个元素作为轴点(通常选择数组尾部或者头部),将小于轴点的元素放在左边,右边自然为大于轴点的元素

    2>递归分解:将数组通过递归不断分解,并调用构造轴点函数,当数组分为一到两个元素时自然有序.

          

下图为构造轴点函数:

//Description  :构造轴点
int partition(int array[],int low,int high)
{
    //以尾元素array[high]作为候选轴
    //进行初次排序,让轴左边的小于轴,右边大于轴,轴为序列最尾端的值
    int i=low-1;
    for (int j=low;j<high;++j)//遍历low到high-1的元素
    {
        if(array[j]<array[high])
        {
            //++i;
            swap(array,++i,j);
        }//array[i]始终小于array[high]
    }
    swap(array,high,(i+1));
    return i+1;
}

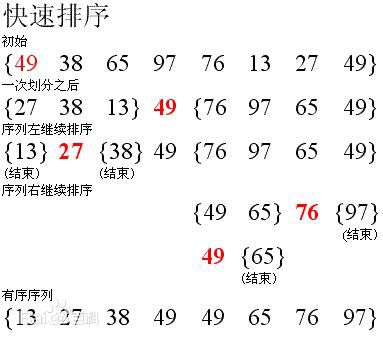
下图是递归排序过程:

void QuickSort(int array[],int low,int high)
{
    if(low>high) return;
// 函数形参中只是传得首地址，不能传数组
    int q=partition(array,low,high);
    QuickSort(array,low,q-1);
    QuickSort(array,q+1,high);
}

3.堆排序步骤:

（1）把待排序数组构造成一个最大堆
（2）取出树的根(最大(小)值, 实际算法的实现并不是真正的取出)
（3）将树中剩下的元素再构造成一个最大堆(这里的构造和第1步不一样，具体看实现部分)
（4）重复2,3操作，直到取完所有的元素
（5）把元素按取出的顺序排列，即得到一个有序数组(在代码实现里是通过交换操作"无形中"完成的)

 下图是建堆过程

/Description  :输入为要被排序的数组和根节点,数组a党组被维护的那部分的下表是low,high
void MaxHeapify(int* a,int i,int low,int high)
{
    int l=left(i);//左子树下标(left(i)=i*2+1)
    int r=right(i);//右子树下标(right(i)=i*2+2)
    int largest=0;//保存左右节点中最大值的下标
    if (l<=high&&a[l]>a[i])
        largest=l;
    else
        largest=i;
    if(r<high && a[r]>a[largest])
        largest=r;
    if(largest!=i)
    {
        //将最大值设为根节点
        swap(a,largest,i);
        //从此次最大节点的位置开始递归堆
        MaxHeapify(a,largest,low,high);
    }
}

下图是堆排序实现

void HeapSort(int a[],int length)
{
    //建立一个大顶堆
    for(int i=length/2-1;i>=0;--i)
        MaxHeapify(a,i,0,length-1);
    for(int i=length-1;i>0;--i)
    {
        swap(a,0,i);//每次将剩余元素的最大值放到最后面
        MaxHeapify(a,0,0,i-1);//因最后元素已为最大值,除去后重新建堆
    }
}

4.排序算法的选择

若从空间复杂度来考虑：

            首选堆排序，其次是快速排序，最后是归并排序。

若从稳定性来考虑：

            应选取归并排序，因为堆排序和快速排序都是不稳定的。

若从平均情况下的排序速度考虑：

            应该选择快速排序。

5.影响快速排序的因素

1>最优情况下的空间复杂度为O(nlogn):轴点每次都平分数组

2>最差情况下时间复杂度为O(n^2):每次取到的轴点元素是数组中最大/最小的,这样就退化成冒泡排序了.